感知机算法基础形式及对偶形式算法
知识预备:
数据线性可分:
对于给定数据集T={(x1,y1),(x2,y2),...,(xn,yn)},;若存在平面wx+b=0将正实例点和负实例点正确划分到两侧,也就是对所有yi=+1的实例,都有wxi+b>0,
对于所有yi=-1的实例,都有都有wxi+b<0;那么就称数据集T为线性可分数据。此外也可以将表现形式转为若yi(wxi+b)>0,则分类正确;若yi(wxi+b)<0分类错误,
从而有若点到面的距离 若小于0,则分类错误,因此将所有错误分类的点到平面的距离进行汇总,得到总距离
若小于0,则分类错误,因此将所有错误分类的点到平面的距离进行汇总,得到总距离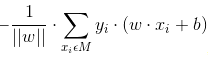 ,不考虑
,不考虑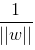 ,则可得到感知机的损失函数。
,则可得到感知机的损失函数。
一、基本算法形式:
输出系数:w,b 感知机模型: f(x)=wx+b
(1) 选取初始值w0,b0
(2)在训练数据集中选取数据(xi,yi),yi为预先给定的样本分类
(3)若yi(wxi+b)≤0 (当yi和wxi+b异号的时候即分类错误,如本应wxi+b大于0一侧的时候,错误分类为yi小于0)
![]()
![]()
通过误分类一侧的点来调整w,b使得分类平面朝误分类点的一侧移动。
(4)转至(2)至训练集中不再出现误分类点
注:感知机算法所得到的平面函数具有不唯一的特点。
二、对偶形式算法:
输入:线性可分的数据集![]() ,其中
,其中![]() ,
,![]() , i=1,2,....N ; 学习率η(0<η≤1);
, i=1,2,....N ; 学习率η(0<η≤1);
输出:a,b; 感知机模型![]() ,其中a=(a1,a2,...,aN)T,yj表示更新的方向,xj表示由误分类点产生的更新长度
,其中a=(a1,a2,...,aN)T,yj表示更新的方向,xj表示由误分类点产生的更新长度
ai=ni*η,ni表示由每个错误分类点产生的分类平面系数的更新次数,η表示分类的步长。
(1) a=0, b=0
(2) 在训练集中选取数据(xi,yi)
(3)如果 ![]() ,则ai=ai+η, b=b+ηyi
,则ai=ai+η, b=b+ηyi
(4)转至(2)直到没有误分类数据


 浙公网安备 33010602011771号
浙公网安备 33010602011771号