如何增加深度学习模型的泛化能力(L1/L2正则化，dropout，数据增强等等)

这是专栏《AI初识境》的第9篇文章。所谓初识，就是对相关技术有基本了解，掌握了基本的使用方法。

今天来说说深度学习中的generalization问题，也就是泛化和正则化有关的内容。

作者&编辑 | 言有三

1 什么是generalization

机器学习方法训练出来一个模型，希望它不仅仅是对于已知的数据(训练集)性能表现良好，对于未知的数据(测试集)也应该表现良好，也就是具有良好的generalization能力，这就是泛化能力。测试集的误差，也被称为泛化误差。

举个例子来说，我们在ImageNet上面训练分类模型，希望这个模型也能正确地分类我们自己拍摄的照片。

在机器学习中，泛化能力的好坏，最直观表现出来的就是模型的过拟合(overfitting)与欠拟合(underfitting)。

过拟合和欠拟合是用于描述模型在训练过程中的两种状态，一般来说，训练会是这样的一个曲线。下面的training error，generalization error分别是训练集和测试集的误差。

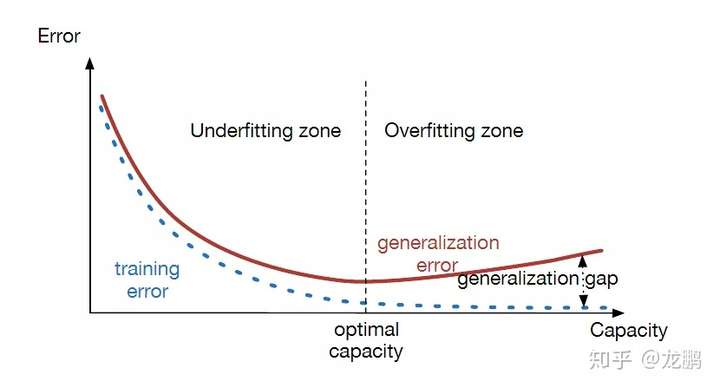
训练刚开始的时候，模型还在学习过程中，训练集和测试集的性能都比较差，这个时候，模型还没有学习到知识，处于欠拟合状态，曲线落在underfitting zone，随着训练的进行，训练误差和测试误差都下降。

随着模型的进一步训练，在训练集上表现的越来越好，终于在突破一个点之后，训练集的误差下降，测试集的误差上升了，这个时候就进入了过拟合区间overfitting zone。

不过也不是说什么训练过程，都会满足上面的曲线。

(1) 模型训练过程中，训练集的误差一定一直低于测试集吗？未必。

如果这两个集合本来就取自于同样的数据分布，比如从一个数据集中随机采样，那么有可能测试的误差从一开始就低于训练集。不过，总体的趋势肯定是不变的，两者从一开始慢慢下降直到最后过拟合，训练集的误差低于测试集。

(2) 模型的训练一定会过拟合吗？这也不一定！

如果数据集足够大，很可能模型的能力不够始终都不会过拟合。另一方面，有很多的方法可以阻止，或者减缓模型的过拟合，比如正则化，这就是下面第二部分要说的。

2 什么是Regularization

Regularization即正则化，它本是代数几何中的一个概念，我们不说因为说不好。放到机器学习里面来说，所谓正则化，它的目标就是要同时让经验风险和模型复杂度较小。

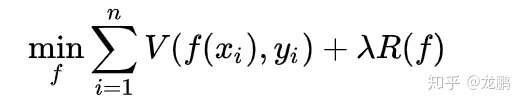
以上是我们的优化目标，V就是损失函数，它表示的是当输入xi预测输出为f(xi)，而真实标签为yi时，应该给出多大的损失。那么我们不禁要问，有这一项不就行了吗？为什么还需要后面的那一项呢？R(f)又是什么呢？

这就是回到上面的泛化误差和过拟合的问题了，一个机器学习系统，学习的是从输入到输出的关系，只要一个模型足够复杂，它是不是可以记住所有的训练集合样本之间的映射，代价就是模型复杂，带来的副作用就是没见过的只是略有不同的样本可能表现地就很差，就像下面这张图，只是更改了一个像素，预测就从Dog变成了Cat。

造成这种情况的问题就是学的太过，参数拟合的太好以致于超过了前面那个训练曲线的最低泛化误差临界点，究其根本原因是模型的表达能力足够强大到过拟合数据集。

式子中的R(f)，正是为了约束模型的表达能力，f是模型，R是一个跟模型复杂度相关的函数，单调递增。

有同学可能会说，模型的表达能力跟模型大小，也就是参数量有关，限制模型的表达能力不是应该去调整模型大小吗？这里咱们从另一个角度来看模型的能力问题。

如果我们限制一层神经网络的参数只能为0或者1，它的表达能力肯定不如不做限制，所以同样的参数量，模型的表达能力与参数本身也有关系，正则项就可以在参数上做文章。

所以说正则化就用于提高模型的泛化能力，这里所说的仅仅是狭义上的参数正则化，而广义上的正则化方法众多，第3部分进行介绍。

正则化的最终目标用一句土话来说，就是让网络学的不要太死，否则变成僵硬的书呆子。

3 正则化方法有哪些

正则化方法，根据具体的使用策略不同，有直接提供正则化约束的参数正则化方法如L1/L2正则化，以及通过工程上的技巧来实现更低泛化误差的方法，比如训练提前终止和模型集成，我将其称为经验正则化，也有不直接提供约束的隐式正则化方法如数据增强等，下面就从这三类进行讲述。

1、经验正则化方法

这里主要包含两种方法，即提前终止和模型集成。

(1) 提前终止

前面我们看的训练曲线随着不断迭代训练误差不断减少，但是泛化误差减少后开始增长。假如我们在泛化误差指标不再提升后，提前结束训练，也是一种正则化方法，这大概是最简单的方法了。

(2) 模型集成

另一种方法就是模型集成(essemable)，也就是通过训练多个模型来完成该任务，它可以是不同网络结构，不同的初始化方法，不同的数据集训练的模型，也可以是用不同的测试图片处理方法，总之，采用多个模型进行投票的策略。

在这一类方法中，有一个非常有名的方法，即Dropout。

Dropout在2014年被H提出后在深度学习模型的训练中被广泛使用。它在训练过程中，随机的丢弃一部分输入，此时丢弃部分对应的参数不会更新。所谓的丢弃，其实就是让激活函数的输出为0。结构示意图如下。

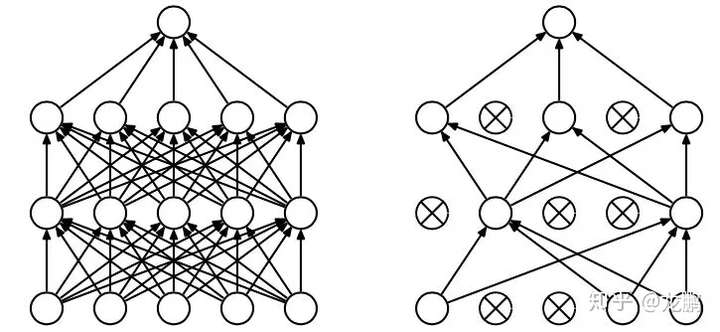
因而，对于一个有n个节点的神经网络，有了dropout后，就可以看做是2^n个模型的集合了，使用的时候当然不能用2^n个模型来进行推理，而是采用了近似方法，即在使用的时候不进行权重丢弃。根据丢弃比例的不同，在测试的时候会给输出乘以相应的系数，比如某一层在训练的时候只保留50%的权重，在测试的时候是需要用到所有参数的，这个时候就给该层的权重乘以0.5。

关于dropout的有效性，从结构上来说，它消除或者减弱了神经元节点间的联合，降低了网络对单个神经元的依赖，从而增强了泛化能力。不过也有另外的一些研究从数据增强的角度来思考这个问题。

那么，就真的不担心dropout会把一些非常重要的神经元删除吗？最新的神经科学的研究以及DeepMind等研究人员通过对神经元进行随机删除来研究网络性能，发现虽然某些神经元确实很重要，它们会选择性激活特定输入，比如只对输入猫图特别敏感，对其他输入则完全不感冒，但是删除这一类神经元仍然不影响网络能识别到猫。

这说明网络中未必少了谁就不行。不过反过来，上面说到的单个像素的攻击，则说明又有某些神经元至关重要。关于这其中的关系，仍然是研究热门，还是不断跟进更多最新的研究吧。

总之一句话，不怕删了谁。就dropout的使用方法而言，我们平常只更改dropout的比例，作者对此还有更多的建议。

(1) 因为dropout降低了模型的性能，所以对于原本需要容量为N的网络才能解决的问题，现在需要N/p，p就是保留该节点的概率，这个概率通常在0.5～0.9之间，p=1就是普通的网络了。

(2) 因为dropout相当于增加了噪声，造成梯度的损失，所以需要使用更大的学习率和动量项。与此同时，对权重进行max-norm等权重约束方法，使其不超过某个值。

(3) 训练更久，很好理解。

对dropout方法，还有很多的变种，包括dropout connect，maxout，stochastic depth等。

一个神经元的输出实际上是由输入以及参数来共同决定，dropout把神经元的值设置为0了，那是不是也可以把参数设置为0呢？这就是drop connect，而且它可以比dropout更加灵活，可视为Dropout的一般化形式，从模型集成的角度来看，Dropout是2^n个模型的平均，那DropConnect呢？它应该更多，因为权重连接的数目比节点数本身更多，所以DropConnect模型平均能力更强。

Drop Connect和Dropout均引入了稀疏性，不同之处在于Drop Connect引入的是权重的稀疏而不是层的输出向量的稀疏。

另外，在dropout这一个思路上做相关文章的还有一些，比如maxout，是一种激活函数，它对N个输入选择最大的作为激活输出。比如随机pooling，是一种池化方法。比如stochastic depth，它用在带有残差结构的网络中，将某些res block直接设置为等价映射。还有backdrop，在前向的时候不drop，在梯度反传的时候才做。

在这里不禁想给大家提两个问题

(1) 你还能想到多少种drop方法？想不到就等我们下次专门说。

(2) dropout应该怎么跟其他的方法结合，比如batch normalization，会强强联合得到更好的结果吗？

2、参数正则化方法

L2/L1正则化方法，就是最常用的正则化方法，它直接来自于传统的机器学习。

L2正则化方法如下：

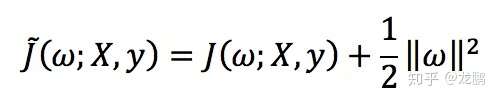
L1正则化方法如下：

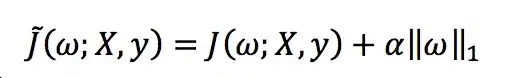
那它们俩有什么区别呢？最流行的一种解释方法来自于模式识别和机器学习经典书籍，下面就是书中的图。

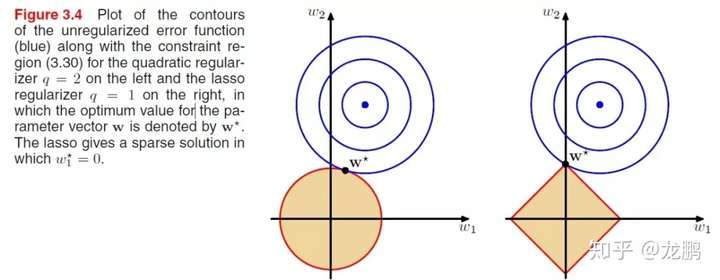
这么来看上面的那张图，参数空间(w1,w2)是一个二维平面，蓝色部分是一个平方损失函数，黄色部分是正则项。

蓝色的那个圈，中心的点其实代表的就是损失函数最优的点，而同心圆则代表不同的参数相同的损失，可见随着圆的扩大，损失增大。黄色的区域也类似，周边的红色线表示的是损失相同点的轮廓。

正则项的红色轮廓线示平方损失的蓝色轮廓线总要相交，才能使得两者加起来的损失最小，两者的所占区域的相对大小，是由权重因子决定的。不管怎么说，它们总有一个交叉点。

对于L2正则化，它的交点会使得w1或者w2的某一个维度特别小，而L1正则化则会使得w1或者w2的某一个维度等于0，因此获得所谓的稀疏化。

在深度学习框架中，大家比起L1范数，更钟爱L2范数，因为它更加平滑和稳定。

3、隐式正则化方法

前面说了两种正则化方法，第一种，通过对网络结构的修改或者在使用方法上进行调整。第二种，直接对损失函数做了修改。这两种方法，其实都应该算作显式的正则化方法，因为在做这件事的过程中， 我们是有意识地知道自己在做正则化。

但是还有另一种正则化方法，它是隐式的正则化方法，并非有意识地直接去做正则化，却甚至能够取得更好的效果，这便是数据有关的操作，包括归一化方法和数据增强，扰乱标签。

关于数据增强的方法，我们以前已经有过几期文章讲述，从有监督方法到无监督方法。关于归一化方法，以batch normalization为代表，我们以前也详细地讲过。参考链接就放这里了，大家自取。

【AI初识境】深度学习模型中的Normalization，你懂了多少？
【技术综述】深度学习中的数据增强（下）
[综述类] 一文道尽深度学习中的数据增强方法（上）

实验表明，隐式的方法比显式的方法更强，从batch normalization的使用替换掉了dropout，以及数据扩增碾压一切trick就可以看出。另外，批量随机梯度算法本身，也可以算是一种隐式的正则化方法，它随机选择批量样本而不是整个数据集，与上面的dropout方法其实也有异曲同工之妙。

这么看来，其实data dependent方法更好，咱们前面的几期都说过，不要闷着头设计，从数据中学习才是王道。

4 深度学习泛化能力到底好不好

你说深度学习的泛化能力是强还是不强，感觉完全可以打一架。

一方面，深度学习方法已经在各行各业落地，说泛化能力不好谁都不信，都已经经得起工业界的考验。关于如何定量的衡量泛化能力，目前从模型复杂度的角度有一些指标，可以参考[1]。

但是另一方面，有许多的研究[2-3]都表明，仅仅是对图像作出小的改动，甚至是一个像素的改动，都会导致那些强大的网络性能的急剧下降，这种不靠谱又让人心慌，在实际应用的过程中，笔者也一直遇到这样的问题，比如下图微小的平移操作对输出概率的严重影响，真的挺常见。

正则化方法可以完美解决吗？甚至最强的数据增强方法能做的都是有限的，一个网络可以记忆住样本和它的随机标签[4]，做什么正则化都没有作用。说起来神经网络一直在力求增强各种不变性，但是却往往搞不定偏移，尺度缩放。这就是为什么在刷比赛的时候，仅仅是对图像采用不同的crop策略，就能胜过任何其他方法的原因，从这一点来说，是一件非常没有意思的事情。

或许，关于正则化，再等等吧。