代价函数，损失函数，目标函数区别
一：损失函数，代价函数，目标函数定义
首先给出结论：
损失函数（Loss Function ）是定义在单个样本上的，算的是一个样本的误差。
代价函数（Cost Function ）是定义在整个训练集上的，是所有样本误差的平均，也就是损失函数的平均。
目标函数（Object Function）定义为：最终需要优化的函数。等于经验风险+结构风险（也就是代价函数 + 正则化项）。代价函数最小化，降低经验风险，正则化项最小化降低
举个例子解释一下:（图片来自Andrew Ng Machine Learning公开课视频）
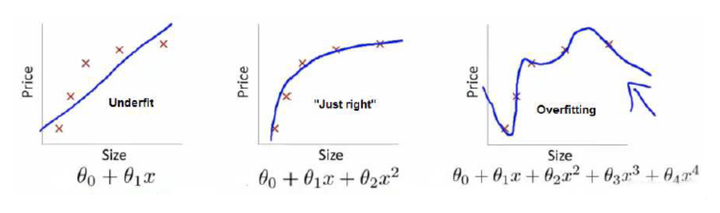
上面三个图的函数依次为f1,f2,f3 。我们是想用这三个函数分别来拟合Price，Price的真实值记为Y 。我们给定x ，这三个函数都会输出一个f(x),这个输出的f(x) 与真实值Y 可能是相同的，也可能是不同的，为了表示我们拟合的好坏，我们就用一个函数来度量拟合的程度，比如：
，这个函数就称为损失函数(loss function)，或者叫代价函数(cost function)（有的地方将损失函数和代价函数没有细分也就是两者等同的）。损失函数越小，就代表模型拟合的越好。
那是不是我们的目标就只是让loss function越小越好呢？还不是。
这个时候还有一个概念叫风险函数(risk function)。风险函数是损失函数的期望，这是由于我们输入输出的(X,Y)遵循一个联合分布，但是这个联合分布是未知的，所以无法计算。但是我们是有历史数据的，就是我们的训练集，f(x) 关于训练集的平均损失称作经验风险(empirical risk)，即
，所以我们的目标就是最小化
称为经验风险最小化。
到这里完了吗？还没有。
如果到这一步就完了的话，那我们看上面的图，那肯定是最右面的f3 的经验风险函数最小了，因为它对历史的数据拟合的最好嘛。但是我们从图上来看f3肯定不是最好的，因为它过度学习历史数据，导致它在真正预测时效果会很不好，这种情况称为过拟合(over-fitting)。
为什么会造成这种结果？大白话说就是它的函数太复杂了，都有四次方了，这就引出了下面的概念，我们不仅要让经验风险尽量小，还要让结构风险尽量小。这个时候就定义了一个函数J(f)，这个函数专门用来度量模型的复杂度，在机器学习中也叫正则化(regularization)。常用的有L1,L2范数。
到这一步我们就可以说我们最终的优化函数是：
，即最优化经验风险和结构风险，而这个函数就被称为目标函数。
结合上面的例子来分析：最左面的f1 结构风险最小（模型结构最简单），但是经验风险最大（对历史数据拟合的最差）；最右面的f3 经验风险最小（对历史数据拟合的最好），但是结构风险最大（模型结构最复杂）;而f2达到了二者的良好平衡，最适合用来预测未知数据集。
??为什么L1,L2范数可以降低模型复杂度
二：详解代价函数
什么是代价函数
假设有训练样本(x, y)，模型为h，参数为θ。h(θ) = θTx（θT表示θ的转置）。
（1）概况来讲，任何能够衡量模型预测出来的值h(θ)与真实值y之间的差异的函数都可以叫做代价函数C(θ)，如果有多个样本，则可以将所有代价函数的取值求均值，记做J(θ)。因此很容易就可以得出以下关于代价函数的性质：
- 对于每种算法来说，代价函数不是唯一的；
- 代价函数是参数θ的函数；
- 总的代价函数J(θ)可以用来评价模型的好坏，代价函数越小说明模型和参数越符合训练样本(x, y)；
- J(θ)是一个标量；
（2）当我们确定了模型h，后面做的所有事情就是训练模型的参数θ。那么什么时候模型的训练才能结束呢？这时候也涉及到代价函数，由于代价函数是用来衡量模型好坏的，我们的目标当然是得到最好的模型（也就是最符合训练样本(x, y)的模型）。因此训练参数的过程就是不断改变θ，从而得到更小的J(θ)的过程。理想情况下，当我们取到代价函数J的最小值时，就得到了最优的参数θ，例如，J(θ) = 0，表示我们的模型完美的拟合了观察的数据，没有任何误差。
（3）在优化参数θ的过程中，最常用的方法是梯度下降，这里的梯度就是代价函数J(θ)对θ1, θ2, ..., θn的偏导数。由于需要求偏导，我们可以得到另一个关于代价函数的性质：
- 选择代价函数时，最好挑选对参数θ可微的函数（全微分存在，偏导数一定存在）
2. 代价函数的常见形式
经过上面的描述，一个好的代价函数需要满足两个最基本的要求：能够评价模型的准确性，对参数θ可微。
2.1 均方误差
在线性回归中，最常用的是均方误差(Mean squared error)，具体形式为：
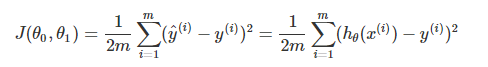
m：训练样本的个数；
hθ(x)：用参数θ和x预测出来的y值；
y：原训练样本中的y值，也就是标准答案
上角标(i)：第i个样本
2.2 交叉熵
损失函数 - 交叉熵损失函数
1. 预测政治倾向例子
我们希望根据一个人的年龄、性别、年收入等相互独立的特征，来预测一个人的政治倾向，有三种可预测结果：民主党、共和党、其他党。假设我们当前有两个逻辑回归模型（参数不同），这两个模型都是通过sigmoid的方式得到对于每个预测结果的概率值：
模型1：
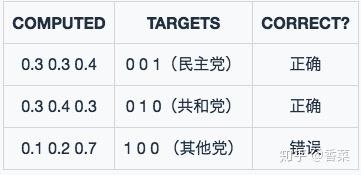模型1预测结果
模型1对于样本1和样本2以非常微弱的优势判断正确，对于样本3的判断则彻底错误。
模型2：
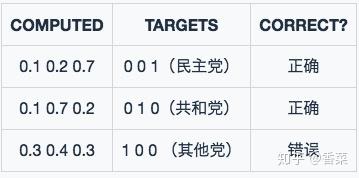模型2预测结果
模型2对于样本1和样本2判断非常准确，对于样本3判断错误，但是相对来说没有错得太离谱。
好了，有了模型之后，我们需要通过定义损失函数来判断模型在样本上的表现了，那么我们可以定义哪些损失函数呢？
1.1 Classification Error（分类错误率）
最为直接的损失函数定义为：
模型1：
模型2：
我们知道，模型1和模型2虽然都是预测错了1个，但是相对来说模型2表现得更好，损失函数值照理来说应该更小，但是，很遗憾的是， 并不能判断出来，所以这种损失函数虽然好理解，但表现不太好。
1.2 Mean Squared Error (均方误差)
均方误差损失也是一种比较常见的损失函数，其定义为：
模型1：
对所有样本的loss求平均：
模型2：
对所有样本的loss求平均：
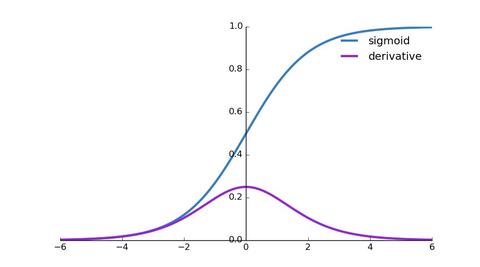
我们发现，MSE能够判断出来模型2优于模型1，那为什么不采样这种损失函数呢？主要原因是逻辑回归配合MSE损失函数时，采用梯度下降法进行学习时，会出现模型一开始训练时，学习速率非常慢的情况（
）。
有了上面的直观分析，我们可以清楚的看到，对于分类问题的损失函数来说，分类错误率和均方误差损失都不是很好的损失函数，下面我们来看一下交叉熵损失函数的表现情况。
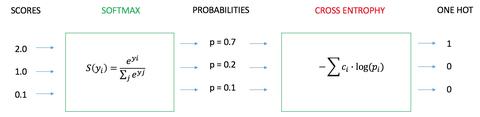
1.3 Cross Entropy Error Function（交叉熵损失函数）
1.3.1 表达式
(1) 二分类
在二分的情况下，模型最后需要预测的结果只有两种情况，对于每个类别我们的预测得到的概率为 和
。此时表达式为：
其中：
- —— 表示样本i的label，正类为1，负类为0
- —— 表示样本i预测为正的概率
(2) 多分类
多分类的情况实际上就是对二分类的扩展：
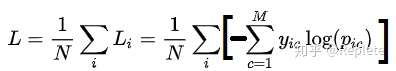
其中：
- ——类别的数量；
- ——指示变量（0或1）,如果该类别和样本i的类别相同就是1，否则是0；
- ——对于观测样本i属于类别
的预测概率。
现在我们利用这个表达式计算上面例子中的损失函数值：
模型1：
对所有样本的loss求平均：
模型2：
对所有样本的loss求平均：
可以发现，交叉熵损失函数可以捕捉到模型1和模型2预测效果的差异。
3 神经网络中的代价函数
学习过神经网络后，发现逻辑回归其实是神经网络的一种特例（没有隐藏层的神经网络）。因此神经网络中的代价函数与逻辑回归中的代价函数非常相似：
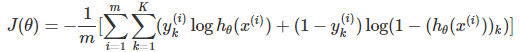
这里之所以多了一层求和项，是因为神经网络的输出一般都不是单一的值，K表示在多分类中的类型数。
