softmax回归
softmax回归
前面介绍的线性回归模型适用于输出为连续值的情景。在另一类情景中,模型输出可以是一个像图像类别这样的离散值。对于这样的离散值预测问题,我们可以使用诸如softmax回归在内的分类模型。和线性回归不同,softmax回归的输出单元从一个变成了多个,且引入了softmax运算使输出更适合离散值的预测和训练。本节以softmax回归模型为例,介绍神经网络中的分类模型。
分类问题
让我们考虑一个简单的图像分类问题,其输入图像的高和宽均为2像素,且色彩为灰度。这样每个像素值都可以用一个标量表示。我们将图像中的4像素分别记为x1,x2,x3,x4x1,x2,x3,x4。假设训练数据集中图像的真实标签为狗、猫或鸡(假设可以用4像素表示出这3种动物),这些标签分别对应离散值y1,y2,y3y1,y2,y3。
我们通常使用离散的数值来表示类别,例如y1=1,y2=2,y3=3y1=1,y2=2,y3=3。如此,一张图像的标签为1、2和3这3个数值中的一个。虽然我们仍然可以使用回归模型来进行建模,并将预测值就近定点化到1、2和3这3个离散值之一,但这种连续值到离散值的转化通常会影响到分类质量。因此我们一般使用更加适合离散值输出的模型来解决分类问题。
softmax回归模型
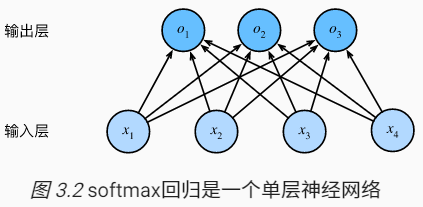
softmax回归跟线性回归一样将输入特征与权重做线性叠加。与线性回归的一个主要不同在于,softmax回归的输出值个数等于标签里的类别数。因为一共有4种特征和3种输出动物类别,所以权重包含12个标量(带下标的ww)、偏差包含3个标量(带下标的bb),且对每个输入计算o1,o2,o3o1,o2,o3这3个输出:

图3.2用神经网络图描绘了上面的计算。softmax回归同线性回归一样,也是一个单层神经网络。由于每个输出o1,o2,o3o1,o2,o3的计算都要依赖于所有的输入x1,x2,x3,x4x1,x2,x3,x4,softmax回归的输出层也是一个全连接层。
softmax运算
然而,直接使用输出层的输出有两个问题。一方面,由于输出层的输出值的范围不确定,我们难以直观上判断这些值的意义。例如,刚才举的例子中的输出值10表示“很置信”图像类别为猫,因为该输出值是其他两类的输出值的100倍。但如果o1=o3=103o1=o3=103,那么输出值10却又表示图像类别为猫的概率很低。另一方面,由于真实标签是离散值,这些离散值与不确定范围的输出值之间的误差难以衡量。
softmax运算符(softmax operator)解决了以上两个问题。它通过下式将输出值变换成值为正且和为1的概率分布:

其中
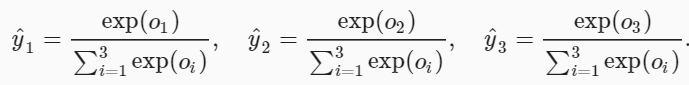

单样本分类的矢量计算表达式
为了提高计算效率,我们可以将单样本分类通过矢量计算来表达。在上面的图像分类问题中,假设softmax回归的权重和偏差参数分别为
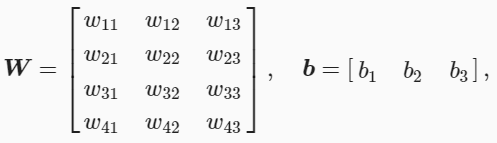

小批量样本分类的矢量计算表达式

交叉熵损失函数





模型预测及评价
在训练好softmax回归模型后,给定任一样本特征,就可以预测每个输出类别的概率。通常,我们把预测概率最大的类别作为输出类别。如果它与真实类别(标签)一致,说明这次预测是正确的。

