寻找图中是否存在路径

有一个具有 n 个顶点的 双向 图，其中每个顶点标记从 0 到 n - 1（包含 0 和 n - 1）。图中的边用一个二维整数数组 edges 表示，其中 edges[i] = [ui, vi] 表示顶点 ui 和顶点 vi 之间的双向边。 每个顶点对由 最多一条 边连接，并且没有顶点存在与自身相连的边。

请你确定是否存在从顶点 source 开始，到顶点 destination 结束的 有效路径 。

给你数组 edges 和整数 n、source 和 destination，如果从 source 到 destination 存在 有效路径 ，则返回 true，否则返回 false 。

示例 1：

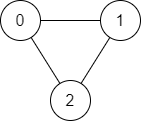
输入：n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2
输出：true
解释：存在由顶点 0 到顶点 2 的路径:

• 0 → 1 → 2
• 0 → 2
  示例 2：
  

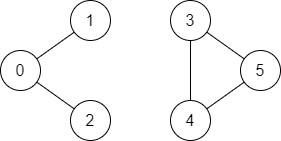
输入：n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5
输出：false
解释：不存在由顶点 0 到顶点 5 的路径.

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/find-if-path-exists-in-graph
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

并查集

class Solution {
    int[] p;
    public boolean validPath(int n, int[][] edges, int source, int destination) {
        //并查集方法:把两个不相交的集合合并为一个集合
        //1.find(x) 函数用于查找 x 所在集合的祖宗节点
        //2.union(a, b) 函数用于合并 a 和 b 所在的集合
        p = new int[n];
        for(int i = 0;i<n;i++){
            p[i] = i;
        }
        union(edges);
        return find(source) == find(destination);
    }
    private void union(int[][] edges){
        for(int[] e : edges){
            //找到x的根和y的根，并且把x做为y的根进行合并
            p[find(e[0])] = find(e[1]);
        }
    }
    private int find(int x){
        //当
        if(p[x]!=x){
            p[x] = find(p[x]);
        }
        return p[x];
    }
}