codeforces计算几何刷题记录【每日一题】

codeforces里面的计算几何我平时都有刷，但是总是懒懒散散的，直到昨天的一场训练赛，作为计算几何选手的我被一道计算几何题卡了几乎整场，虽然这题是防ak题，但赛后补出来发现并不是很难，主要原因还是我计算几何太弱了。于是乎，蒟蒻我下定决心从今天开始，每天至少刷一道计算几何（其他时间可能要补补cf或者学学其他算法的，所以就不强制整天练计几了）。

以此记录！！codeforces 的problemset，tag选择计算几何，按照难度排序，从第一篇最后一题往上刷。加油！！！。

 （后补：发现cf上面有些计几题其实考察的不是计几，所以就挑一些比较计几的计几题来做了，然后也不局限于cf了，反正每天坚持一道不水的计几就好了）

https://codeforces.com/problemset/page/1?tags=geometry&order=BY_RATING_DESC

开始！！

2020.4.6： 第一题：Delivering Carcinogen

二分然后套个圆的板子就ok了。

#include<bits/stdc++.h>
using namespace std;
#define eps 1e-6
const double pi = acos(-1.0);
struct Point{
    double x,y,v;
    Point rotate(double deta){
        return (Point){ x * cos(deta) - y*sin(deta),x*sin(deta) + y * cos(deta)};
    }
}a,b;
double dist(Point a,Point b){
    return sqrt( (a.x - b.x)*(a.x - b.x) + (a.y - b.y)*(a.y-b.y));
}
double cross(Point a,Point b,Point c){
    return (b.x - a.x) * (c.y-a.y) - (c.x - a.x) * (b.y - a.y);
}
struct Circle{
    Point o;
    double r;
    //圆心出发的射线的交点
    Point getPoint(double deta){
        return (Point){o.x + cos(deta)*r , o.y + sin(deta)*r};
    }
    //两个圆上的点的最短圆弧
    double getPointDis(Point a,Point b){
        double deta = fabs( atan2(a.y - o.y,a.x - o.x) - atan2(b.y - o.y,b.x - o.x));
        deta = min(deta,2*pi - deta);
        return deta * r;
    }
    //ab线段和圆是否相交
    bool is_insert(Point a,Point b){
        double ab = dist(a,b);
        double d = fabs(cross(o,a,b)) / ab;
        if( d > r - eps) return 0;
        double oa = dist(a,o) , ob = dist(o,b);
        double ta = (oa*oa + ab*ab - ob*ob)/2*oa*ab;
        double tb = (ob*ob + ab*ab - oa*oa)/2*oa*ab;
        if(ta < -eps || tb < -eps) return 0;
        return 1;
    }
}cir;
//求切点
void getTangentPoints(Point p,Circle C , Point& r1,Point& r2){
    double d = dist(p,C.o);
    double base = atan2(p.y - C.o.y,p.x - C.o.x);
    double deta = acos( C.r/d );
    r1 = C.getPoint(base - deta);
    r2 = C.getPoint(base + deta);
}
int sgn(double x){
    if( fabs(x) < eps) return 0;
    if( x > 0) return 1;
    return -1;
}
bool judge(double t){
    double R = sqrt( a.x * a.x + a.y * a.y);
    double w = a.v / R ;
    Point c = a.rotate(w * t);
    if(cir.is_insert(b,c) == 0 ) return dist(b,c) < t*b.v + eps;
    Point cutb1 , cutb2;
    getTangentPoints(b,cir,cutb1,cutb2);
    Point cutc1 , cutc2;
    getTangentPoints(c,cir,cutc1,cutc2);
    double tem1 = dist(b,cutb2) + dist(c,cutc1) + cir.getPointDis(cutb2,cutc1); 
    double tem2 = dist(b,cutb1) + dist(c,cutc2) + cir.getPointDis(cutb1,cutc2);
    return min( tem1,tem2 ) < t*b.v + eps;
}
int main(){
    scanf("%lf %lf %lf",&a.x,&a.y,&a.v);
    scanf("%lf %lf %lf %lf",&b.x,&b.y,&b.v,&cir.r);
    cir.o = (Point){0,0};
    double le = 0 , ri = 100000000;
    double res;
    while( ri - le > eps){
        double m = (ri+le)/2;
        if(judge(m)){
            res = m;
            ri = m;
        }
        else le = m;
    }
    printf("%.9f",res);
    return 0;
}

 

2020.4.7：第二题：Kingdom Trip （K题）

这题我们把两两是否有边建立出来，然后直接来个n方dp就好了。问题是怎么建边。

我们判断线段ab和圆是否有交，其实是判断圆心到线段距离<R，并且两个非圆心夹角是锐角。然后其实我们还可以过a做圆o的切线，判断b是否在o切线夹角里面，那么假如ab在圆同一侧呢？没关系，我们反过来再做一次判断就好了。具体判断就是，枚举起点i，然后依次往后判断j，然后判断完j之后，把 j 的切线夹角和原来的求个交就好了。

然后其实判断夹角交有一个很好的做法就是：我们把第一个角度ph0设为基准，然后夹角范围我们用相对于ph0的deta来表示，左夹角为ph0 + l , 右夹角为 ph0 + r，那么我们每一次要交的是夹角角度是

[ phj - deta , phj + deta] ,那么我们只需要判断phj 和 ph0 之间的绝对夹角 theta， 然后   l = max(l,theta-deta);     r = min(r,theta+deta); 即可。

这样比那种直接把左右角度表示出来好很多，因为左右角度表示出来很容易出现 l >r ，烦得要死。

#include<bits/stdc++.h>
using namespace std;
#define eps 1e-7
const int N = 2e3+9;
#define inf 1e8
const double pi = acos(-1.0);
struct Point{
    double x,y;
}p[N];
int dp[N],G[N][N];
double cross(Point a,Point b,Point c){
    return (b.x-a.x)*(c.y-a.x) - (c.x-a.x)*(b.y-a.y);
}
double dist(Point a,Point b){
    return sqrt((a.x-b.x)*(a.x-b.x) + (a.y-b.y)*(a.y-b.y));
}
int n; 
double d;
double solve(double x){
    if(x>pi+eps) return x - 2*pi;
    if(x<-pi - eps) return x + 2*pi;
    return x;
}
void init(bool fg){
    for(int i = 1;i<n;++i){
        double ph0 = inf,l,r;
        for(int j = i+1;j<=n;++j){
            double dd = dist(p[i],p[j]);
            bool ok = 1;
            double phj = atan2(p[j].y-p[i].y,p[j].x-p[i].x);
            double theta = solve(phj-ph0);
            if(ph0 != inf){
                if(theta < l - eps || theta > r + eps) ok = 0;
            }
            if(ok){
                if(fg) G[i][j] = 1;
                else G[n+1-i][n+1-j] = 1;
            }
            if(dd < d - eps) continue;
            double deta = asin(d/dd);
            if(ph0 == inf){
                ph0 = phj;
                l = -deta;
                r = deta;
            }
            else{
                l = max(l,theta-deta);
                r = min(r,theta+deta);
            }
        }
    }
}
void work(){
    memset(dp,127,sizeof(dp));
    dp[n] = 1;
    for(int i = n-1;i>=1;--i){
        for(int j = i+1;j<=n;++j){
            if(G[i][j] && G[j][i]) dp[i] = min(dp[i],dp[j] + 1);
        }
    }
    printf("%d",dp[1]);
}
int main(){
    freopen("kingdom.in", "r", stdin);
    freopen("kingdom.out", "w", stdout);
    scanf("%d %lf",&n,&d);
    for(int i = 1;i<=n;++i) scanf("%lf %lf",&p[i].x,&p[i].y);
    init(0);
    reverse(p+1,p+1+n);
    init(1);
    // for(int i = 1;i<=n;++i){
    //     for(int j = 1;j<=n;++j){
    //         cerr<<i<<" "<<j<<" "<<G[i][j]<<endl;
    //     }
    // }
    work();
    return 0;
}

 

2020.4.8 第三题 ： Split Game

第一象限给你一个简单多边形，问你从原点连一条射线，能分成多边形最多多少份

很明显就是扫描线啦，极角排序然后扫描线，按照每一个点与左右两边的点的位置关系来判断是+1还是-1，需要注意的是，我们平时的扫描线是把+1的放前，-1放后，贪心。但是这里我们不能贪心，一定得把这条线答案统计完再更新答案。还有就是，有一些点是扫描线到这点就更新，有一些点是到这个点之后才更新，所以给他一个fr标记，标记它的前后。

也不是很难。。。。

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+9;
typedef long long ll;
struct Point{
    ll x,y;
    int id,ty,fr;
    ll len(){return x*x+y*y;}
}p[N],tem[N],p0;
ll cross(Point a,Point b,Point c){
    return (b.x-a.x)*(c.y-a.y) - (c.x-a.x)*(b.y-a.y);
}
bool cmp(Point a,Point b){
    if(cross(p0,a,b) == 0 ) return a.fr > b.fr;
    return cross(p0,a,b) > 0;
}
int n; 
void init(){
    int nn = 0;
    p[nn++] = tem[0];
    for(int i = 1;i<n;++i){
        while( nn >= 2 && cross(p[nn-2],p[nn-1],tem[i]) == 0 ){
            --nn;
        }
        p[nn++] = tem[i]; 
    }
    n = nn;
}
int main(){
    scanf("%d",&n);
    p0.x = p0.y = 0;
    for(int i = 0;i<n;++i){
        scanf("%lld %lld",&tem[i].x,&tem[i].y);
    }
    init();
    for(int i = 0;i<n;++i) p[i].id = i;
    for(int i = 0;i<n;++i){
        Point l = p[ (i - 1 + n ) % n];
        Point r = p[ (i + 1 ) % n];
        ll cl = cross(p0,p[i],l) , cr = cross(p0,p[i],r);
        if( cl > 0 && cr > 0 ){
            p[i].ty = 1;
            if(cross(p[i],l,r) > 0 ) p[i].fr = 1;
            else p[i].fr = -1;
        }
        else if( cl < 0 && cr < 0 ){
            p[i].ty = -1;
            if(cross(p[i],l,r) > 0 ) p[i].fr = -1;
            else p[i].fr = 1;
        }
        else if(cl == 0){
            Point llp = p[ (i - 2 + n ) % n];
            ll cll = cross(p0,p[i],llp);
            if(cll > 0 && cr > 0) p[i].ty = 1;
            else if( cll < 0 && cr < 0 ) p[i].ty = -1;
            if(l.len() < p[i].len()) p[i].fr = -1;
            else p[i].fr = 1;
        }
    }
    ll ans = 1, now = 1;
    sort(p,p+n,cmp);
    for(int i = 0;i<n;++i){
        // cerr<<p[i].x<<" "<<p[i].y<<" "<<p[i].ty<<" "<<p[i].fr<<endl;
        if( i > 0 && cross(p0,p[i],p[i-1]) == 0 && p[i].fr == p[i-1].fr ) now += p[i].ty;
        else{
            ans = max(now,ans);
            now += p[i].ty;
        }
    }
    ans = max(ans,now);
    printf("%d",ans);
    return 0;
}

 

2020.4.10 第四题：Alice and Bomb

题意：二维平面有一个点是光源，有n个简单多边形，问从原点走到阴影处最短距离

昨天咕咕咕了一天，今天补回来。这题其实就是一个寻路问题，寻路问题就是扣关键点，然后对关键点连边，最后跑最短路。这题最终答案肯定是走某一条垂线，所以直接跑最短路，连边就是各个顶点以及垂足。

#include<bits/stdc++.h>
using namespace std;
#define eps 1e-6
const double inf = 1e30;
const double pi = acos(-1.0);
struct Point{
    double x,y;
    double dis;
    bool ok;
    int id;
    Point(){}
    Point(double xx,double yy){
        x = xx; y = yy;
    }
    bool operator < (const Point& b)const{
        return dis > b.dis;
    }
    Point operator + (const Point& b)const{
        return (Point){x+b.x,y+b.y};
    }
    Point operator * (const double& b)const{
        return (Point){b*x,b*y};
    }
}p0,A;
struct Line{
    Point s,e;
    double a,b,c;
    Line(Point p1,Point p2){
        s = p1, e = p2;
        a = p2.y - p1.y;
        b = p1.x - p2.x;
        c = p2.x * p1.y - p1.x * p2.y;
    }
};
int n; 
const int N = 1000+9;
vector<Point> pol[N];
double dis[N][N];
double ans[N];
bool can[N];
int cnt;
int sgn(double x){
    if(fabs(x) < eps ) return 0;
    if(x>0) return 1;
    return -1;
}
double dist(Point a,Point b){
    return sqrt( (a.x-b.x)*(a.x-b.x) + (a.y-b.y)*(a.y-b.y));
}
double cross(Point a,Point b,Point c){
    return (b.x - a.x)*(c.y-a.y) - (c.x-a.x)*(b.y-a.y);
}
double dot(Point a,Point b,Point c){
    return (b.x - a.x) * (c.x - a.x) + (b.y - a.y) * (c.y - a.y);
}
Point footOfLine(Line l,Point p){
    double t = (l.a * p.x + l.b*p.y + l.c) / (l.a * l.a + l.b * l.b);
    return p + Point(l.a,l.b) * t;
}
bool insert(Line l1,Line l2){
    return 
        max(l1.s.x,l1.e.x) >= min(l2.s.x,l2.e.x) &&
        max(l2.s.x,l2.e.x) >= min(l1.s.x,l1.e.x) &&
        max(l1.s.y,l1.e.y) >= min(l2.s.y,l2.e.y) &&
        max(l2.s.y,l2.e.y) >= min(l1.s.y,l1.e.y) &&
        sgn( cross(l1.s,l2.s,l1.e) ) * sgn( cross(l1.s,l2.e,l1.e)) < 0 &&
        sgn( cross(l2.s,l1.s,l2.e) ) * sgn( cross(l2.s,l1.e,l2.e)) < 0;
}
bool access(Point a,Point b){
    Line l1 = Line(a,b);
    for(int i = 1;i<=n;++i){
        for(int k = 0;k<pol[i].size()-1;++k){
            Line l2 = Line(pol[i][k],pol[i][k+1]);
            // cerr<<l2.s.x<<" "<<l2.s.y<<" "<<l2.e.x<<" "<<l2.e.y<<endl;
            if( insert(l1,l2) ) return 0;
            // cerr<<"hh"<<endl;
        }
    }
    return 1;
}
void solve(){
    for(int i = 1;i<=cnt;++i){
        for(int j = i+1;j<=cnt;++j){
            dis[i][j] = dis[j][i] = inf;
        }
    }
    for(int i = 1;i<=n;++i){
        for(int j = i+1;j<=n;++j){
            for(int a = 0;a<pol[i].size()-1;++a){
                for(int b = 0;b<pol[j].size()-1;++b){
                    if(access(pol[i][a],pol[j][b])){
                        dis[pol[i][a].id][pol[j][b].id] = dis[pol[j][b].id][pol[i][a].id] = dist(pol[i][a],pol[j][b]);
                    }
                    dis[pol[i][a].id][pol[j][b].id] = dis[pol[j][b].id][pol[i][a].id] = inf;
                }
            }
        }
    }
    for(int i = 1;i<=n;++i){
        for(int j = 0;j<pol[i].size()-1;++j){
            dis[pol[i][j].id][pol[i][j+1].id] = dis[pol[i][j+1].id][pol[i][j].id] = dist(pol[i][j],pol[i][j+1]);
        }
    }
    for(int i = 1;i<=n;++i){
        for(int j = 0;j<pol[i].size() - 1;++j){
            if(cross(p0,pol[i][j],pol[i][j+1]) > eps){
                can[pol[i][j].id] = can[pol[i][j+1].id] = 1;
                // cerr<<"can"<<endl;
            }
        }
    }
    priority_queue<Point> q;
    A.dis = 0;
    A.ok = A.id = 0; 
    q.push(A);
    while(!q.empty()){
        Point now = q.top();
        q.pop();
        // cerr<<now.x<<" "<<now.y<<" "<<now.dis<<" "<<now.ok<<" now"<<endl;
        if(now.ok){
            // cerr<<now.x<<" "<<now.y<<endl;
            printf("%.8f\n",now.dis);
            break;
        }
        for(int i = 1;i<=n;++i){
            for(int k = 0;k<pol[i].size() - 1;++k){
                int idb = pol[i][k].id;
                if(now.id){
                    if(dis[now.id][idb] != inf && now.dis + dis[now.id][idb] < ans[idb]){
                        ans[idb] = now.dis + dis[now.id][idb];
                        Point tem = pol[i][k];
                        tem.dis = ans[idb];
                        tem.ok = 0;
                        // cerr<<tem.dis<<" "<<tem.x<<" "<<tem.y<<" ans"<<endl;
                        q.push(tem);
                    }
                }
                else{
                    if(access(now,pol[i][k]) && now.dis + dist(pol[i][k],now) < ans[idb]){
                        ans[idb] = now.dis + dist(now,pol[i][k]);
                        // cerr<<idb<<" "<<dist(pol[i][k],now)<<endl;
                        Point tem = pol[i][k];
                        tem.dis = ans[idb];
                        tem.ok = 0;
                        // cerr<<tem.x<<" "<<tem.y<<" "<<tem.dis<<" idb"<<endl;
                        q.push(tem);
                    }
                }
            }
        }
        for(int i = 1;i<=n;++i){
            for(int k = 0;k<pol[i].size()-1;++k){
                if(can[pol[i][k].id] && ( dot(pol[i][k],p0,now) < eps) ){
                    Point tem = footOfLine(Line(p0,pol[i][k]) , now );
                    tem.dis = now.dis + dist(now,tem);
                    // cerr<<"okk"<<endl;
                    // cerr<<tem.dis<<endl;
                    tem.id =  0 , tem.ok = 1;
                    // cerr<<tem.x<<" "<<tem.y<<" "<<tem.dis<<" tem"<<endl;
                    q.push(tem);
                }
            }
        }
    }
    // cerr<<"fuck"<<endl;
}
int main(){
    // cerr<<sqrt(5)<<endl;
    A.x = 0, A.y = 0;
    while(~scanf("%d",&n) && n){
        cnt = 0;
        scanf("%lf %lf",&p0.x,&p0.y);
        for(int i = 1;i<=n;++i){
            pol[i].clear();
            int m; scanf("%d",&m);
            Point tem;
            for(int j = 1;j<=m;++j){
                scanf("%lf %lf",&tem.x,&tem.y);
                tem.id = ++cnt;
                ans[cnt] = inf;
                can[cnt] = 0;
                pol[i].push_back(tem);
            }
            pol[i].push_back(pol[i][0]);
        }
        if(access(p0,A) == 0){
            printf("0.00000000\n");
            continue;
        }
        // cerr<<"here"<<endl;
        solve();
    }
}

 

2020.4.11 第五题：Symmetry

题意：给你一个简单多边形，顺序乱序，问你这个是否轴对称图形。

我们枚举第一个点的对称点，然后再On判断即可，记得还要判断轴上的点是否大于2个。

假如第一个点在轴上？没关系，因为轴上的点不可能大于2个，不然多边形自交，所以我们同样工作做三次即可。

#include<bits/stdc++.h>
using namespace std;
#define eps 1e-6
const double inf = 1e30;
const int N = 1000+8;
const double pi = acos(-1.0);
struct Point{
    double x,y;
    Point operator - (const Point& b)const{
        return (Point){x-b.x,y-b.y};
    }
    Point operator + (const Point& b)const{
        return (Point){x+b.x,y+b.y};
    }
    Point operator * (const double& b)const{
        return (Point){b*x,b*y};
    }
    bool operator < (const Point& b)const{
        if(x == b.x) return y < b.y;
        return x < b.x;
    }
    double mul(const Point& b)const{
        return x*b.x + b.y*y;
    }
    void near(){
        int cx = ceil(x) , fx = floor(x);
        int cy = ceil(y) , fy = floor(y);
        if( fabs(cx - x) < eps ) x = cx;
        else if(fabs(fx - x) < eps) x = fx;
        else x = inf;
        
        if(fabs(cy - y) < eps) y = cy;
        else if(fabs(fy - y) < eps ) y = fy;
        else y = inf;
    }
}p[N];
bool show;
struct Line{
    Point s,e;
};
map<Point,int> has;
int n; 
int sgn(double x){
    if(fabs(x) < eps ) return 0;
    if( x>0 ) return 1;
    return -1;
}
double cross(Point a,Point b,Point c){
    return (b.x-a.x)*(c.y-a.y) - (c.x-a.x)*(b.y-a.y);
}
double dist2(Point a,Point b){
    return (a.x-b.x)*(a.x-b.x) + (a.y-b.y)*(a.y-b.y);
}
double dot(Point a,Point b,Point c){
    return (b.x-a.x)*(c.x-a.x) + (b.y-a.y)*(c.y-a.y);
}
Point projection(Line l,Point p){
    double t = dot(l.s,p,l.e) / dist2(l.s,l.e);
    return l.s + (l.e - l.s) * t;
}
Point reflection(Line l,Point p){
    return p + (projection(l,p) - p) * 2;
}
bool onLine(Point a,Point b,Point c){
    return sgn(cross(a,b,c)) == 0;
}
bool judge(Point s,Point e,Point a,Point b){
    Point mid = (a+b)*0.5;
    return onLine(s,e,mid) && (sgn( (e-s).mul(b-a) ) == 0) ;
}
bool solve(){
    int cnt = 0;
    for(int cas = 1;cas<=3;++cas){
        for(int k = 2;k<=n;++k){
            cnt = 0;
            Point a = (p[1] + p[k]) * 0.5;
            Point b = p[k] - p[1];
            swap(b.x,b.y);
            b.x = -b.x;
            b = a + b;
            Line l = (Line){a,b};
            for(int i = 1;i<=n;++i) has[ p[i] ] = 1;
            has[ p[1] ] = has[ p[k] ] = 0;
            bool ok = 1;
            for(int i = 1;i<=n && ok;++i){
                if(has[p[i]] == 0) continue;
                Point tem = reflection(l,p[i]);
                tem.near();
                if(tem.x == inf || tem.y == inf || (has[tem] == 0)) ok = 0;
                if(judge(l.s,l.e,p[i],tem) == 0) ok = 0;
                has[tem] = has[p[i]] = 0;
                if(tem.x == p[i].x && tem.y == p[i].y) ++cnt;
            }
            if(ok && cnt<=2) return 1;
        }

        Point tem = p[1];
        for(int i =1;i<n;++i) p[i] = p[i+1];
        p[n] = tem;
    }
    return 0;
}
bool all_Line(){
    for(int i = 3;i<=n;++i){
        if( sgn( cross(p[1],p[2],p[i]) ) != 0 ) return 0;
    }
    return 1;
}
int main(){
    scanf("%d",&n);
    for(int i =  1;i<=n;++i) scanf("%lf %lf",&p[i].x,&p[i].y);
    if(all_Line()){
        puts("No");
        return 0;
    }
    if(solve()) puts("Yes");
    else puts("No");
    return 0;
}

 

2020.4.12 第六题：集训队训练：Forest protection

这题虽然到最后很少人过，但是其实很简单，直接当作签到题秒了，就求个凸包然后旋转卡壳一下好了。。

#include<bits/stdc++.h>
using namespace  std;
typedef long long ll;
const int N = 1e5+9;
struct Point{
    ll x,y;
    bool operator < (const Point& b)const{
        return x < b.x || (x==b.x && y < b.y);
    }
    Point operator - (const Point& b)const{
        return (Point){x-b.x,y-b.y};
    }
    ll cro(Point b){
        return x*b.y - b.x*y;
    }
    ll dot(Point b){
        return x*b.x + y * b.y;
    }
}p[N],ch[N*2];
int n; 
ll cross(Point a,Point b,Point c){
    return (b.x - a.x)*(c.y-a.y) - (c.x-a.x)*(b.y-a.y);
}
int Andrew(){
    sort(p,p+n);
    int m = 0;
    for(int i = 0;i<n;++i){
        while( m>1 && cross(ch[m-2],p[i],ch[m-1]) > 0 ) --m;
        ch[m++] = p[i];
    }
    int k = m;
    for(int i = n-2;i>=0;--i){
        while( m>k && cross(ch[m-2],p[i],ch[m-1]) >0 ) --m;
        ch[m++] = p[i];
    }
    if(n>1) --m;
    return m;
}
bool all_line(){
    for(int i = 2;i<n;++i){
        if(cross(p[0],p[1],p[i]) != 0) return 0;
    }
    return 1;
}
int main(){
    scanf("%d",&n);
    for(int i = 0;i<n;++i) scanf("%lld %lld",&p[i].x,&p[i].y);
    if( all_line() ){
        printf("%d",n);
        return 0;
    }
    int m = Andrew();
    int ans = 0;
    for(int i = 0;i<m;++i) ch[i+m] = ch[i];
    int j = 0;
    for(int i = 0;i<m;++i){
        while( j<i+m && ( ( (ch[i+1] - ch[i]).cro(ch[j+1] - ch[j]) == 0) && ( ch[i+1] - ch[i]).dot(ch[j+1] - ch[j]) > 0 ) ) ++j;
        while( j < i+m && (ch[i+1] - ch[i]).cro(ch[j+1] - ch[j]) > 0 ) ++j;
        // cerr<<ch[i].x<<" "<<ch[i].y<<" "<<ch[j].x<<" "<<ch[j].y<<" "<<i<<" "<<j<<endl;
        ans = max(j - i -1,ans);
    }
    printf("%d",m - ans);
    return 0;
}

 

2020.4.13 第七题（H）： Cornering at Poles

题意：给你8个圆，问你从原点走到终点，不能经过任意圆的最短距离。

这题是一道寻路问题的经典题目。其实不是很难，但是老是写挂细节，搞得心态崩了。。。写了两天。

就是很明显，我两个点的最短距离肯定就是点到圆的切线，圆上的弧，两圆切线。可以想像一下一根直线拉直。

然后就是把模板抄上去，建图跑dij就好了。 注意：弧上两点判断是否可以达到，只需要判断两个点是不是在某一个圆里，或者某一个圆的圆心极角在 两点极角之间，然后 可以那部分圆弧就取min就好了。

可以把关键点全部扣出来，然后n方建边，也可以边扣关键点边建边。

#include<bits/stdc++.h>
using namespace std;
#define eps 1e-8
#define pii pair<double,int> 
const double inf = 1e50;
const double pi = acos(-1.0);
const int N = 1e5+9;
double R;
int sgn(double x){
    if(fabs(x) < eps) return 0;
    if( x > 0 ) return 1;
    return -1;
} 
struct Point{
    double x,y;
    Point operator - (const Point& b)const{
        return (Point){x-b.x,y-b.y};
    }
    Point operator + (const Point& b)const{
        return (Point){ x + b.x,y+b.y};
    }
    Point operator * (const double& b)const{
        return (Point){x*b,y*b};
    }
    Point operator / (const double& b)const{
        return (Point){x/b,y/b};
    }
}p[N];

double cross(Point a,Point b,Point c){
    return (b.x-a.x)*(c.y-a.y) - (c.x-a.x)*(b.y-a.y);
}
double dot(Point a,Point b,Point c){
    return (b.x - a.x)*(c.x-a.x) + (b.y-a.y)*(c.y-a.y);
}
double dist2(Point a,Point b){
    return (a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y);
}
double dist(Point a,Point b){
    return sqrt(dist2(a,b));
}
double Point_to_Seg(Point p,Point a,Point b){
    if( sgn( dot(a,p,b) ) < 0 ) return dist(p,a);
    if( sgn( dot(b,p,a) ) < 0 ) return dist(p,b);
    return fabs( cross(p,a,b) ) / dist(a,b);
}
struct Circle{
    Point o;
    vector<int> v;
    Point getPoint(double deta){
        return (Point){o.x + cos(deta)*R , o.y + sin(deta)*R };
    }
    bool is_insert(Point a,Point b){
        double d;
        if( dist(a,b) < eps ) d = dist(a,o);
        else d = Point_to_Seg(o,a,b);
        if( sgn(d  - R) < 0 ) return 1;
        return 0;
    }
}cir[10];
int cnt;
int bel[N];
vector< pair<int,double> > G[N];
double dis[N];
Point a[10],b[10];
int n; 
int getTangentPoints(Point p,Circle c,Point& r1,Point& r2){
    double d = dist(p,c.o);
    if( sgn(d-R) < 0 ) return 0;
    else if( sgn(d-R) == 0 ){
        r1 = p;        
        return 1;
    }
    else{
        double base = atan2(p.y - c.o.y,p.x - c.o.x);
        double deta = acos( R/d );
        r1 = c.getPoint(base - deta);
        r2 = c.getPoint(base + deta);
        return 2;
    }
}
int getCircleTangents(Circle A,Circle B,Point* a,Point* b){
    int cnt = 0;
    double d2 = dist2(A.o,B.o);
    double rsum = 2*R;
    double base = atan2(B.o.y - A.o.y,B.o.x - A.o.x);
    double ang = acos(0.0);
    a[cnt] = A.getPoint(base+ang); b[cnt] = B.getPoint(base+ang); cnt++;
    a[cnt] = A.getPoint(base-ang); b[cnt] = B.getPoint(base-ang); cnt++;

    if( sgn(d2 - rsum*rsum) > 0 ){
        ang = acos( 2*R/ sqrt(d2) );
        a[cnt] = A.getPoint(base + ang); b[cnt] = B.getPoint(pi+base + ang); ++cnt;
        a[cnt] = A.getPoint(base - ang); b[cnt] = B.getPoint(pi+base - ang); ++cnt;
    }
    return cnt;
}
bool road_ok(Point a,Point b){
    for(int i = 1;i<=n;++i){
        if( cir[i].is_insert(a,b) ) return 0;
    }
    return 1;
}
// double relative(double a){
//     if( a < -pi ) a += 2*pi;
//     else if( a > pi) a -= 2*pi;
//     return a;
// }
double rad_ok(int k,Point a,Point b){
    Circle c = cir[k];
    double le = atan2(a.y - c.o.y,a.x - c.o.x);
    double ri = atan2(b.y - c.o.y,b.x - c.o.x);
    if( le > ri ) swap(le,ri);
    bool ok1 = 1, ok2 = 1;
    for(int i = 1;i<=n;++i){
        if( dist(a,cir[i].o) < R - eps || dist( b,cir[i].o) < R - eps ) return inf;
        double d = dist(cir[i].o,cir[k].o);
        if( i == k || dist(cir[i].o,c.o) > 2*R - eps) continue;
        Point w = (cir[i].o - cir[k].o) / d * 100.0 + cir[k].o;
        // double phi = atan2( cir[i].o.y - c.o.y , cir[i].o.x - c.o.x);
        double phi = atan2(w.y-c.o.y,w.x - c.o.x);
        if( sgn(phi - le) > 0  && sgn(phi - ri) < 0 ) ok1 = 0;
        else ok2 = 0;
    }
    double res = inf;
    // cerr<<(ri-le)*R<<" "<<(2*pi - ri + le)*R<<" !!!"<<ok1<<" "<<ok2<<endl;
    if(ok1) res = min(res,(ri - le)*R );
    if(ok2) res = min(res, (2*pi - ri + le) * R);
    return res;
}
void build_G(){
    for(int i = 1;i<=n;++i){
        Point r1,r2;
        int m = getTangentPoints(p[1],cir[i],r1,r2);
        if( m == 0 ) return;
        if(m>=1 ){
            p[++cnt] = r1; bel[cnt] = i;
        }
        if(m >= 2){
            p[++cnt] = r2; bel[cnt] = i;
        }

        m = getTangentPoints(p[2],cir[i],r1,r2);
        if( m == 0 ) return;
        if(m>=1 ){
            p[++cnt] = r1; bel[cnt] = i;
        }
        if(m >= 2){
            p[++cnt] = r2; bel[cnt] = i;
        }
    }

    for(int i = 1;i<=n;++i){
        for(int j = i+1;j<=n;++j){
            int m = getCircleTangents(cir[i],cir[j],a,b);
            for(int k = 0;k<m;++k){
                    p[++cnt] = a[k]; bel[cnt] = i;
                    p[++cnt] = b[k]; bel[cnt] = j;
            }
        }
    }
    for(int i = 1;i<=cnt;++i){
        for(int j = i+1;j<=cnt;++j){
            if( bel[i] == bel[j] ){
                double d = rad_ok(bel[i],p[i],p[j]);
                // cerr<<i<<" "<<j<<" "<<d<<endl;
                if( d != inf ){
                    G[i].push_back({j,d});
                    G[j].push_back({i,d});
                }
            }
            else{    
                if(road_ok(p[i],p[j])){
                    G[i].push_back({j,dist(p[i],p[j])});
                    G[j].push_back({i,dist(p[i],p[j])});
                }
            }
        }
    }
}
void dij(){
    for(int i = 1;i<=cnt;++i) dis[i] = inf;
    dis[1] = 0;
    priority_queue<pii,vector<pii>,greater<pii> > q;
    q.push(make_pair(0,1));
    while(!q.empty()){
        int u = q.top().second;
        double tem = q.top().first;
        q.pop();
        if( tem > dis[u] + eps ) continue;
        for(auto it : G[u]){
            int v = it.first;
            double w = it.second;
            if( dis[v] - eps > dis[u] + w){
                dis[v] = dis[u] + w;
                q.push( make_pair(dis[v],v) );
            }
        }
    }
}
int main(){
    R = 100.0;
    scanf("%d",&n);
    scanf("%lf %lf",&p[2].x,&p[2].y);
    p[1].x = p[1].y = 0;
    bel[1] = 0 , bel[2] = n+1;
    cnt = 2;
    for(int i = 1;i<=n;++i){
        scanf("%lf %lf",&cir[i].o.x,&cir[i].o.y);
    }
    build_G();
    dij();

    if( dis[2] == inf ) printf("0.0");
    else printf("%.5f",dis[2]);
    return 0;
}
/*
1 958 834
86 57
*/

 

2020.4.15.第八题：hdu4785

这题真的难顶，前前后后挂了很多次，可能也是因为晚上思维下降的原因吧。为这题专门写了一个博客：https://www.cnblogs.com/xiaobuxie/p/12712701.html

#include<bits/stdc++.h>
using namespace std;
#define eps 1e-8
const int N = 1e3+9;
const double inf = 1e6;
int sgn(double x){
    if( fabs(x) < eps) return 0;
    if( x < 0 ) return -1;
    return 1;
}
struct Point{
    double x,y;
    Point operator - (const Point& b)const{
        return (Point){x-b.x,y-b.y};
    }
    Point operator + (const Point& b)const{
        return (Point){x+b.x,y+b.y};
    }
    bool operator < (const Point& b)const{
        if( sgn(x - b.x) == 0 ) return y < b.y;
        return x < b.x;
    }
}va[N],vb[N],rec[10];
double cross(Point a,Point b){
    return a.x * b.y - b.x * a.y;
}
vector<Point> a[N],b[N];
int n;
double xl,yl,xr,yr;
double X[N];
double mi[N],mx[N];
int cnt;
bool insert(Point a,Point b,Point c,Point d){
    return 
        max(a.x,b.x) >= min(c.x,d.x) &&
        max(c.x,d.x) >= min(a.x,b.x) &&
        max(a.y,b.y) >= min(c.y,d.y) &&
        max(c.y,d.y) >= min(a.y,b.y) &&
        sgn(cross(c-a,b-a))*sgn(cross(d-a,b-a))<=0 &&
        sgn(cross(a-c,d-c))*sgn(cross(b-c,d-c))<=0;
}
Point segcross(Point a,Point b,Point c,Point d){
    double u = cross(b-a,c-a) , v = cross(a-b,d-b);
    return (Point){ (c.x*v+d.x*u)/(u+v) , (c.y*v+d.y*u)/(u+v)};
}
vector<Point> Minke(vector<Point> pa,vector<Point> pb){
    int na = pa.size(),nb = pb.size();
    //
    int ida = 0, idb = 0;
    for(int i = 0;i<na;++i) if(pa[i] < pa[ida]) ida = i;
    for(int i = 0;i<nb;++i) if(pb[i] < pb[idb]) idb = i;
    vector<Point> ta , tb;
    for(int i = 0;i<na;++i){
        ta.push_back(pa[ida]);
        ida = (ida+1)%na;
    }
    for(int i = 0;i<nb;++i){
        tb.push_back(pb[idb]);
        idb = (idb+1)%nb;
    }
    pa = ta; pb = tb;

    for(int i = 0 ; i < na-1;++i) va[i] = pa[i+1] - pa[i];
    va[na-1] = pa[0] - pa[na-1];
    for(int i = 0 ; i < nb-1;++i) vb[i] = pb[i+1] - pb[i];
    vb[nb-1] = pb[0] - pb[nb-1];
    vector<Point> pc;
    Point tem;
    tem = pa[0] + pb[0];
    pc.push_back(tem);
    int p1 = 0, p2 = 0;
    while(p1 < na && p2 < nb){
        tem = tem + ( (cross(va[p1],vb[p2]) >= 0 ) ? va[p1++] : vb[p2++]);
        pc.push_back(tem);
    }
    while(p1 < na){
        tem = tem + va[p1++];
        pc.push_back(tem);
    }
    while(p2 < nb){
        tem = tem + vb[p2++];
        pc.push_back(tem);
    }
    //
    return pc;
}
void init(){
    double xmi = a[n+1][0].x,ymi = a[n+1][0].y,xmx = xmi , ymx = ymi;
    for(auto it : a[n+1]){
        xmi = min(xmi,it.x) , xmx = max(xmx,it.x);
        ymi = min(ymi,it.y) , ymx = max(ymx,it.y);
    }
    xl -= xmi; xr -= xmx;
    yl -= ymi; yr -= ymx;

    for(int i = 0;i<a[n+1].size();++i){
        a[n+1][i].x = -a[n+1][i].x;
        a[n+1][i].y = -a[n+1][i].y;
    }
    for(int i = 1;i<=n;++i){
        b[i] = Minke(a[n+1],a[i]);
    }
    for(int i = 1;i<=n;++i){
        mi[i] = b[i][0].x , mx[i] = mi[i];
        for(auto it : b[i]){
            mi[i] = min(mi[i],it.x);
            mx[i] = max(mx[i],it.x);
        }
    }
    X[++cnt] = xl;
    X[++cnt] = xr;
    for(int i = 1;i<=n;++i){
        for(auto it : b[i]){
            if(it.x < xl + eps || it.x > xr - eps ) continue;
            X[++cnt] = it.x;
        }
    }
    for(int i = 1;i<=n;++i){
        for(int j = i+1;j<=n;++j){
            for(int ii = 0;ii<b[i].size()-1;++ii){
                for(int jj = 0;jj<b[j].size()-1;++jj){
                    Point s1 = b[i][ii] , e1 = b[i][ii+1];
                    Point s2 = b[j][jj] , e2 = b[j][jj+1];
                    if( sgn(cross(e1 - s1,s2 - s1) ) == 0 && sgn(cross(e1 - s1,e2 - s1) == 0 ) ) continue;
                    if( insert(s1,e1,s2,e2) ){
                        Point tem = segcross(s1,e1,s2,e2);
                        if(tem.x < xl + eps || tem.x > xr - eps ) continue;
                        X[++cnt] = tem.x;
                    }
                }
            }
        }
    }
    rec[0] = (Point){xl,yl}; rec[1] = (Point){xr,yl};
    rec[2] = (Point){xr,yr}; rec[3] = (Point){xl,yr}; rec[4] = rec[0];
    for(int i = 1;i<=n;++i){
        for(int j = 0;j<b[i].size()-1;++j){
            for(int k = 0;k<4;++k){
                if(insert(b[i][j],b[i][j+1],rec[k],rec[k+1])){
                    Point res = segcross(b[i][j],b[i][j+1],rec[k],rec[k+1]);
                    X[++cnt] = res.x;
                }
            }
        }
    }
    sort(X+1,X+1+cnt);
}
void crosspol(vector<Point> p, double xx , vector< pair<double,int> >& Y){
    Point le = (Point){xx,-inf} , ri = (Point){xx,inf};
    vector<double> vec;
    for(int j = 0;j<p.size()-1;++j){
        if( sgn( p[j].x - le.x) == 0 && sgn(p[j+1].x - le.x) == 0){
            vec.push_back(p[j].y);
            vec.push_back(p[j+1].y);
        }
        else{
            if(insert(le,ri,p[j],p[j+1]) ){
                Point tem = segcross(le,ri,p[j],p[j+1]);
                vec.push_back(tem.y);
            }
        }
    }
    sort(vec.begin(),vec.end());
    if(vec.size() < 2) return;
    double ya = vec[0] , yb = vec[vec.size()-1];
    Y.push_back({max(ya,yl),1}); Y.push_back({min(yb,yr),-1});
}
double solve_len(vector< pair<double,int> > Y){
    sort(Y.begin(),Y.end());
    int num = 0;
    double res = 0;
    double las;
    for(auto it : Y){
        if(num==0 && it.second == 1){
            las = it.first;
            ++num;
            continue;
        }
        num += it.second;
        if(num == 0 && it.second == -1) res += (it.first - las);
    }
    return res;
}
void solve(){
    double ans = 0;
    for(int i = 1;i<cnt;++i){
        vector< pair<double,int> > Yl,Yr;
        for(int j = 1;j<=n;++j){
            if(mx[j] < X[i] + eps || mi[j] > X[i+1] - eps ) continue;
            crosspol(b[j],X[i],Yl);
            crosspol(b[j],X[i+1],Yr);
        }
        double le = solve_len(Yl) , ri = solve_len(Yr);
        ans += (ri + le) * (X[i+1] - X[i]) * 0.5;
    }
    printf("%.3f\n",(xr-xl)*(yr-yl) - ans);
    return;
}
int main(){
    int T; scanf("%d",&T);
    for(int cas = 1;cas <= T;++cas){
        cnt = 0;
        printf("Case #%d: ",cas);
        scanf("%d",&n);
        for(int i = 1;i<=n+1;++i){
            a[i].clear();
            int m; scanf("%d",&m);
            for(int j = 1;j<=m;++j){
                Point tem;
                scanf("%lf %lf",&tem.x,&tem.y);
                a[i].push_back(tem);
            }
        }
        scanf("%lf %lf %lf %lf",&xl,&yl,&xr,&yr);
        init();
        solve();
    }
    return 0;
}
/*
6
1
3
0 0
10 0
10 10
4
0 0
1 0
1 1
0 1
0 0 10 10
*/

 

2020.4.19 第九题：http://codeforces.com/group/uVAsoW2Jkj/contest/276618

这是我们的训练赛。 I 题是计几，题意：空间给你两个三角形，判断两个三角形最短距离。

由于我没有三维计几板子，然后直接炸裂，被迫写了个三分，（因为答案肯定是一个边和一个面距离，所以三分边，转换成点到三角形距离，然后T成傻逼了，结束之后队友爬山算法加各种优化帮我2.8s卡过去了）。

正解：先判断三角形是否相交，相交就0，否则就是顶点到另一个三角形距离，以及线段距离，这个很显然。然后就是上板子的事情了。

#include<bits/stdc++.h>
using namespace std;
#define eps 1e-7
const double pi = acos(-1.0);
int sgn(double x){
    if( fabs(x) < eps ) return 0;
    if( x > 0 ) return 1;
    return -1;
}
struct Point{
    double x,y,z;
    Point operator - (const Point& b)const{
        return (Point){x-b.x,y-b.y,z-b.z};
    }
    Point operator + (const Point& b)const{
        return (Point){x+b.x,y+b.y,z+b.z};
    }
    Point operator * (const double& b)const{
        return (Point){b*x,b*y,b*z};
    }
    Point operator / (const double& b)const{
        return (Point){x/b,y/b,z/b};
    }
    double len(){return sqrt(x*x+y*y+z*z); }
}T1[4],T2[4];
Point cross(Point a,Point b){
    double xx = a.y*b.z-b.y*a.z;
    double yy = a.x*b.z-b.x*a.z;
    double zz = a.x*b.y-b.x*a.y;
    return (Point){xx,-yy,zz};
}
double dot(Point a,Point b){
    return a.x*b.x + a.y*b.y + a.z*b.z;
}

bool SameSide(Point p1,Point p2,Point a,Point b){
    return dot(cross(b - a, p1 - a), cross(b - a, p2 - a)) - eps >= 0;
}
bool PointInTri(Point P, Point P0, Point P1,Point P2){
    return SameSide(P, P0, P1, P2) && SameSide(P, P1, P0, P2) && SameSide(P, P2, P0, P1);
}

// 三角形P0P1P2是否和线段AB相交
bool TriSegIntersection(Point P0, Point P1,  Point P2, Point A, Point B, Point & P){
    Point n = cross(P1 - P0, P2 - P0);
    if(abs(dot(n, B - A)) <= eps)  return false;    // 线段A-B和平面P0P1P2平行或共面
    else   // 平面A和直线P1-P2有惟一交点
    {
        double t = dot(n, P0 - A) / dot(n, B - A);
        if(t + eps < 0 || t - 1 - eps > 0)  return false;    // 不在线段AB上
        P = A + (B - A) * t; // 交点
        return PointInTri(P, P0, P1, P2);
    }
}
//空间两三角形是否相交
bool TriTriIntersection(Point * T1, Point * T2){
    Point P;
    for(int i = 0; i < 3; i++){
        if(TriSegIntersection(T1[0], T1[1], T1[2], T2[i], T2[(i + 1) % 3], P))
        {
            return true;
        }
 
        if(TriSegIntersection(T2[0], T2[1], T2[2], T1[i], T1[(i + 1) % 3], P))
        {
            return true;
        }
    }
 
    return false;
}


//点到线段的距离
double point_to_seg(Point p, Point a, Point b){
    if((a-b).len()<eps) return (p - a).len();          //xiugai
    Point v1 = b - a, v2 = p - a, v3 = p - b;
    if(dot(v1, v2) + eps < 0)  return v2.len();
    else{
        if(dot(v1, v3) - eps > 0) return v3.len();
        else return cross(v1, v2).len() / v1.len();
    }
}


double point_to_tri(Point p,Point a,Point b,Point c){
    if(PointInTri(p,a,b,c)){
        Point n = cross(b-a,c-a);
        return fabs( dot( p-a ,n ) ) / n.len() ;
    }
    else{
        double res = point_to_seg(p,a,b);
        res = min(res,point_to_seg(p,a,c));
        res = min(res,point_to_seg(p,b,c));
        return res;
    }
}

// // 两线段距离
// double SegDis(Point a, Point b, Point c, Point d) {
//     Point n = cross(a - b, c - d);
//     if (sgn(n.len()) != 0) {
//         n = n / n.len();                                                /// xiugai
//         Point cc = GetPlaneProjection(c, a, n);
//         Point dd = GetPlaneProjection(d, a, n);
//         Point res;
//         if (SegCross(a, b, cc, dd, res) == 1)
//             return LineDis(a, b, c, d);
//     }
//     double ret = point_to_seg(a, c, d);
//     ret = min(ret, point_to_seg(b, c, d));
//     ret = min(ret, point_to_seg(c, a, b));
//     ret = min(ret, point_to_seg(d, a, b));
//     return ret;
// }

//线段之间距离 
double seg_to_seg(Point a,Point b,Point c,Point d){
    double res = min( point_to_seg(a,c,d) , point_to_seg(b,c,d) );
    res = min( res , min( point_to_seg(c,a,b) , point_to_seg(d,a,b) ) );
    Point normal = cross(b-a, d-c);
    double cp1 = dot(normal, cross( d-c, a-c) );
    double cp2 = dot(normal, cross( d-c, b-c) );
    double cp3 = dot(normal, cross( b-a, c-a) );
    double cp4 = dot(normal, cross( b-a, d-a) );
    if (cp1*cp2 < -eps && cp3*cp4 < -eps ) {
        Point p1 = (b*cp1 - a*cp2) / (cp1-cp2);
        Point p2 = (d*cp3 - c*cp4) / (cp3-cp4);
        res = min(res, (p2-p1).len());
    }
    return res;
}
          
int main(){
    int T; scanf("%d",&T);
    while(T--){
        scanf("%lf %lf %lf %lf %lf %lf %lf %lf %lf",&T1[0].x,&T1[0].y,&T1[0].z,&T1[1].x,&T1[1].y,&T1[1].z,&T1[2].x,&T1[2].y,&T1[2].z);
        scanf("%lf %lf %lf %lf %lf %lf %lf %lf %lf",&T2[0].x,&T2[0].y,&T2[0].z,&T2[1].x,&T2[1].y,&T2[1].z,&T2[2].x,&T2[2].y,&T2[2].z);
        if(TriTriIntersection(T1,T2)){
            printf("0.000000000\n");
            continue;
        }
        double ans = 1e60;
        for(int i = 0;i<3;++i) ans = min(ans,point_to_tri(T1[i],T2[0],T2[1],T2[2]) );
        for(int i = 0;i<3;++i) ans = min(ans,point_to_tri(T2[i],T1[0],T1[1],T1[2]) );
        for(int i = 0;i<3;++i){
            for(int j = 0;j<3;++j){
                ans = min(ans,seg_to_seg(T1[i],T1[(i+1)%3] , T2[j],T2[(j+1)%3]));
            }
        }
        printf("%.9f\n",ans);
    }
    return 0;
}

 

2020.4.20 第十题：cf1218B

这题就是给你n个仓库（凸多边形），原点有个镭射眼，可以透过一面墙看到仓库，问你看到仓库的最大面积是多少。

这题其实就直接是扫面线，因为两个线段的相对位置不会因为扫描线改变而改变，所以我们用set来维护靠近原点最近的线段，然后每次往set里面加减线段，找前两个线段统计答案就好。

这题不知道为什么一定要用long double 才能过。。。。。卡了很久，，，，

#include<bits/stdc++.h>
using namespace std;
const int N = 5e4+8;
#define double long double
const double eps = 1e-9;
const double pi = acos(-1.0);
const double inf = 1e6;
int cnt;
int segcnt = 0;
double curang;
struct Point{
    double x,y;
    double corss(Point b)const{
        return x * b.y - b.x * y;
    }
    Point operator - (const Point& b)const{
        return (Point){x-b.x,y-b.y};
    }
    double len(){return sqrt(x*x+y*y);}
};
Point segcross(Point a,Point b,Point c,Point d,bool& ok ){
    double u = (b-a).corss(c-a) , v = (a-b).corss(d-b);
    if( fabs(u+v) < eps){
        ok = 0;
        Point tem = {-1,-1};
        return tem;
    }
    ok = 1;
    return (Point){ (c.x*v + d.x*u)/(u+v) , (c.y*v + d.y*u)/(u+v) };
}
struct Seg{
    Point a,b;
    int id;
    bool operator < (const Seg& s)const{
        bool ok1 ,ok2;
        Point c = (Point){cos(curang) , sin(curang)};
        Point o = (Point){0,0};
        Point cr1 = segcross(a,b,o,c,ok1);
        Point cr2 = segcross(s.a,s.b,o,c,ok2);
        // if( ok1 == 0 || ok2 == 0 ) return id < s.id;
        // assert(ok1 && ok2);
        if( fabs( cr1.len() - cr2.len() ) < eps ) return id < s.id;
        return cr1.len() < cr2.len();
    }
};
vector<Point> pol[N];
double ang[N];
vector<int> add[N],del[N];
Seg seg[N];

void add_seg(Point a,Point b){
    double anga = atan2(a.y,a.x) , angb = atan2(b.y,b.x);
    if( fabs(anga - angb) < eps ) return;
    if( anga > angb + eps ){
        swap(anga,angb);
        swap(a,b);
    }
    int pa = lower_bound(ang+1,ang+1+cnt,anga) - ang;
    int pb = lower_bound(ang+1,ang+1+cnt,angb) - ang;

    ++segcnt;
    seg[segcnt] = (Seg){a,b,segcnt};
    if( angb - anga > pi + eps ){
        // Point c = segcross(a,b,(Point){-inf,0},(Point){inf,0});
        if( fabs(anga + pi) > eps){
            // ++segcnt;
            // seg[segcnt] = (Seg){c,a,segcnt};
            add[1].push_back(segcnt);
            del[pa].push_back(segcnt);
        }

        if( fabs( angb - pi ) > eps){
            // ++segcnt;
            // seg[segcnt] = (Seg){b,c,segcnt};
            add[pb].push_back(segcnt);
            del[cnt].push_back(segcnt);
        }
    }
    else{
        add[pa].push_back(segcnt);
        del[pb].push_back(segcnt);
    }
}
double area(Point a,Point b,Point c,Point d){
    double res = 0;
    res += (b-a).corss(c-a);
    res += (c-a).corss(d-a);
    if(res < -eps ) res = -res;
    return res * 0.5;
}
void solve(){
    set<Seg> st;
    double ans = 0;
    curang = 0;
    for(int i = 1;i<cnt;++i){
        for(auto it : del[i] )  st.erase(seg[it]);
        curang = ( ang[i] + ang[i+1] ) / 2.0;
        for(auto it : add[i])  st.insert(seg[it]);
        if((int)st.size() >= 2){
            // assert((int)st.size()>=2);
            Seg s1,s2;
            auto it = st.begin();  s1 = (*it);
            ++it; s2 = (*it);
            Point c1 = (Point){inf*cos(ang[i]) , inf * sin(ang[i])};
            Point c2 = (Point){inf*cos(ang[i+1]) , inf * sin(ang[i+1])};
            Point o = (Point){0,0};
            bool ok1,ok2,ok3,ok4;
            Point a1 = segcross(o,c1,s1.a,s1.b,ok1);
            Point a2 = segcross(o,c1,s2.a,s2.b,ok2);
            Point a3 = segcross(o,c2,s2.a,s2.b,ok3);
            Point a4 = segcross(o,c2,s1.a,s1.b,ok4);
            // assert(ok1 && ok2 && ok3 && ok4);
            // if( ok1 == 0 || ok2 == 0 || ok3 == 0 || ok4 == 0) continue;
            ans += area(a1,a2,a3,a4);
        }
    }
    // printf("%.12f",ans);
    cout<<ans<<endl;
}
int main(){
    int n; cin>>n;
    for(int i = 1;i<=n;++i){
        int m; cin>>m;
        Point tem;
        for(int j = 1;j<=m;++j){
            // scanf("%lf %lf",&tem.x,&tem.y);
            cin>>tem.x>>tem.y;
            // cerr<<tem.x<<" "<<tem.y<<" !"<<endl;
            pol[i].push_back(tem);
            ang[++cnt] = atan2(tem.y,tem.x);
        }
        pol[i].push_back(pol[i][0]);
    }
    ang[++cnt] = -pi; ang[++cnt] = pi;
    sort(ang+1,ang+1+cnt);
    cnt = unique(ang+1,ang+1+cnt) - ang - 1;

    for(int i = 1;i<=n;++i){
        for(int k = 0;k<pol[i].size()-1;++k){
            add_seg(pol[i][k],pol[i][k+1]);
        }
    }
    
    solve();
    return 0;
}

 

2020.4.22 第十一题：hdu4805

这题卡了我一天了，这题不知道为什么会挂，然后对着过了的代码改，发现好像是std写挂了？？？不知道，反着这题挺奇怪的。

#include<bits/stdc++.h>
using namespace std;
#define eps 1e-9
// #define double long double
const int N = 1e5+9;
bool vis[N];
int sgn(double x){
    if( fabs(x) < eps) return 0;
    if( x < 0 ) return -1;
    return 1;
}
// double ans,stlen;
struct Point{
    double x,y,z;
    Point operator - (const Point& b)const{
        return (Point){x-b.x,y-b.y,z-b.z};
    }
    Point operator * (const double& b)const{
        return (Point){x*b,y*b,z*b};
    }
    Point operator / (const double& b)const{
        return (Point){x/b,y/b,z/b};
    }
    Point operator + (const Point& b)const{
        return (Point){x+b.x,y+b.y,z+b.z};
    }
    double len(){return sqrt(x*x+y*y+z*z);}
    double len2(){return x*x+y*y+z*z;}
}S,T,dir,Tri[N][5];
int n;
Point cross(Point A, Point B) {
    return Point{A.y * B.z - A.z * B.y, A.z * B.x - A.x * B.z, A.x * B.y - A.y * B.x};
}
double dot(Point a,Point b){
    return a.x * b.x + a.y * b.y + a.z* b.z;
}
//点是否在线段上(包括顶点)
bool Point_on_Seg(Point p,Point a,Point b){
    return sgn( dot(a-p,b-p) ) <=0 && sgn( cross(a-p,b-p).len() ) == 0;
}
//点是否在直线上
bool Point_on_Line(Point p,Point a,Point b){
    return cross(p-a,b-a).len() < eps;
}
bool intersect(Point a,Point b,Point c,Point d){
    return sgn( dot( cross(b-a,c-a) , cross(b-a,d-a) ) ) <= 0 && sgn( dot( cross(d-c,a-c) ,cross(d-c,b-c))) <= 0;
}
bool parallel(Point a,Point b,Point c,Point d){
    return sgn( cross(a-b,c-d).len() ) == 0;
}
//直线相交判定 0:不相交(平行); 1:规范相交; 2:非规范相交(重合); 3:异面不相交 
int LineCross(Point a, Point b, Point c, Point d, Point &res) {
    // Point n = cross(b - a, d - c);
    Point n = dir;
    if ( sgn(dot( n, c - a) ) != 0) return 3;
    if (sgn(n.len()) == 0) {
        if (sgn(cross(a - b, c - b).len()) == 0) return 2;
        return 0;
    }
    n = d + n;
    Point f = cross(d - c, n - c);
    double t = dot(f, c - a) / dot(f, b - a);
    res = a + (b - a) * t;
    return 1;
}

// 线段相交判定 0:不相交; 1:规范相交; 2:非规范相交(包含端点),3:重合
int SegCross(Point a, Point b, Point c, Point d,Point &res) {
    int k = LineCross(a, b, c, d, res);
    if (k == 0 || k == 3) return 0;
    if (k == 1) {
        double d1 = dot(a - res, b - res);
        double d2 = dot(c - res, d - res);
        if (d1 < -eps && d2 < -eps ) return 1;
        if ( (sgn(d1) == 0  && d2 < eps) || (sgn(d2) == 0 && d1 < eps) ) return 2; //包含端点
        return 0;
    }
    if (dot(a - c, b - c) <= 0 || dot(a - d, b - d) <= 0
        || dot(c - a, d - a) <= 0 || dot(c - b, d - b) <= 0)
        return 3;
    return 0;
}
// p1和p2是否在线段a-b的同侧,(p1,p2,a,b 同一平面)
// p1,p2,a,b不同平面时，表示p1ab,p2ab两个半平面夹角是否锐角
bool SameSide(Point  p1,Point p2,Point  a,Point b){
    return dot(cross(b - a, p1 - a), cross(b - a, p2 - a)) > -eps ;
}
// 点P在三角形P0, P1, P2中 (p,p0,p1,p2 同一平面)
// p和p0p1,p2不同一面时，判断点p是否在p0,p1,p2形成的三角形柱形内
bool PointInTri(Point P,Point  P0,Point  P1,Point  P2){
    return SameSide(P, P0, P1, P2) && SameSide(P, P1, P0, P2) && SameSide(P, P2, P0, P1);
}
bool In(Point p,Point a,Point b,Point c){
    if( parallel(a,b,a,c) ){
        return Point_on_Seg(p,a,b) || Point_on_Seg(p,a,c) || Point_on_Seg(p,b,c);
    }
    Point ta = cross(b-a,p-a);
    Point tb = cross(c-b,p-b);
    Point tc = cross(a-c,p-c);
    return sgn(dot(ta,tb))>=0 && sgn(dot(tb,tc))>=0 && sgn(dot(ta,tc))>=0;
}
// 点在平面上的投影
Point point_plane_projection(Point p, Point p0, Point n) {
    double d = dot(p - p0, n) ;
    return p - n * d / n.len2();
}
double judge( int id){
    if( cross(Tri[id][0]-S,T-S).len() < eps ){
        double tmp = 0;
        for(int i = 0;i<3;++i){
            Point a = Tri[id][i] , b = Tri[id][(i+1)%3];
            if( Point_on_Seg(T,a,b) ){
                if( Point_on_Seg(S,a,b) ) tmp = max(tmp,(S-T).len());
                if( Point_on_Seg(a,S,T) ) tmp = max(tmp,(a-T).len());
                if( Point_on_Seg(b,S,T) ) tmp = max(tmp,(b-T).len());
            }
            if( Point_on_Seg(a,S,T) && Point_on_Seg(b,S,T) ) return (b-a).len();
        }
        return tmp;
    }
    return 0;
}

Point line_make_point(Point ua,Point ub,Point va,Point vb){
    double t = ( (ua.x-va.x)*(va.y-vb.y)-(ua.y-va.y)*(va.x-vb.x) )
                / ((ua.x-ub.x)*(va.y-vb.y)-(ua.y-ub.y)*(va.x-vb.x));
    return ua + (ub-ua)*t;
}
double solve(Point s,Point t,Point a,Point b){
    if( !parallel(s,t,a,b) ){
        if( !intersect(s,t,a,b) ) return 0;
        Point tem = line_make_point(s,t,a,b);
        return (tem-t).len();
    }
    if( sgn(cross(t-s,b-s).len() )!= 0 ) return 0;
    if( Point_on_Seg(t,a,b) ){
        double tem = 0;
        if( Point_on_Seg(a,s,t) ) tem = max(tem,(a-t).len());
        if( Point_on_Seg(b,s,t) ) tem = max(tem,(b-t).len());
        return tem;
    }
    if( Point_on_Seg(a,s,t) && Point_on_Seg(b,s,t)) return (b-a).len();
    return 0;
}

void work(){
    double ans = 0;
    for(int i = 1;i<=n;++i){
        bool Sin = In(S,Tri[i][0],Tri[i][1],Tri[i][2]);
        bool Tin = In(T,Tri[i][0],Tri[i][1],Tri[i][2]);
        if( Sin && Tin ){
            ans += (T-S).len();
            // continue;
        }
        if( Sin ){
            swap(S,T);
            swap(Sin,Tin);
        }
        if(vis[i]){
            // if( Sin && Tin ) ans += (T-S).len();
            ans += judge(i);
            continue;
        }    
        else if(  Tin ){
            if( Sin && Tin ) continue;
            double tem = 0;
            for(int k = 0;k<3;++k){
                Point a = Tri[i][k] , b = Tri[i][(k+1)%3];
                Point res;
                int tet = SegCross(a,b,S,T,res);
                if( tet == 1 || tet == 2){
                    SegCross(a,b,S,T,res);
                    tem = max(tem,(res-T).len());
                }
            }
            ans += tem;
        }
        else{
            if( Sin && Tin ) continue;
            vector<Point> res;
            for(int k = 0;k<3;++k){
                Point a = Tri[i][k] , b = Tri[i][(k+1)%3];
                Point tem;
                int tet = SegCross(S,T,a,b,tem);
                if( tet == 1 || tet == 2) res.push_back(tem);
            }
            if( res.size()  ) ans += (res[1] - res[0]).len();
        }
    }
    ans /= (T-S).len();
    printf("%.8f\n",ans);
}
int main(){
    while(~scanf("%d",&n)){
        scanf("%lf %lf %lf",&S.x,&S.y,&S.z);
        scanf("%lf %lf %lf",&T.x,&T.y,&T.z);
        scanf("%lf %lf %lf",&dir.x,&dir.y,&dir.z);
        for(int i = 1;i<=n;++i){
            vis[i] = 0;
            scanf("%lf %lf %lf",&Tri[i][0].x,&Tri[i][0].y,&Tri[i][0].z);
            scanf("%lf %lf %lf",&Tri[i][1].x,&Tri[i][1].y,&Tri[i][1].z);
            scanf("%lf %lf %lf",&Tri[i][2].x,&Tri[i][2].y,&Tri[i][2].z);
            if( sgn( dot( cross(Tri[i][1] - Tri[i][0],Tri[i][2]-Tri[i][0]) , dir) ) == 0 ) vis[i] = 1;
            for(int j = 0;j<3;++j){
                Tri[i][j] = point_plane_projection(Tri[i][j],S,dir);
            }
        }
        if( sgn( cross(T-S,dir).len() ) == 0 ){
            double ans = 0;
            for(int i = 1;i<=n;++i){
                if(In(S,Tri[i][0],Tri[i][1],Tri[i][2]) ) ans = ans+1;
            }
            printf("%.8f\n",ans);
            continue;
        }
        T = point_plane_projection(T,S,dir);
        work();
    }
    return 0;
}

 

2020.4.23 第十二题 ：codeforces1146H

题意：二维平面给你300个点，没有三点共线，问你能构造多少个五角星（不一定规则五角星）。

这题开始想了个假算法，后来就秒了。 首先五角星转换为严格凸五边形。然后dp[i] [j] [k] 代表 i 一直链接到 j 其中有 k 个线段。最后直接 sigama dp[i][i][5]即可。

我们只需要把所有线段极角排序，然后枚举每一个线段，每个线段（s，t）加进来的时候，直接把 dp[s] 转移到 dp[t] 即可。

正确性：显然，一个五边形是能够从最顶端的那条边一直转移过来的，那么会不会统计多了呢？不会！因为假如一个虚假的五边形被统计，比如说四边形加一条重边，画个图就知道是不会统计进答案的。

总结：一开始我是打算分开每个点来统计答案，但是这样有个问题就是保证不了凸性，也就是线段的斜率不保证单调，这就很难搞。而且枚举每个点的话，只能固定起点，终点没固定的话就可能会绕回来导致重边，所以我的dp一定是有两维分别是起点终点。然后我对于所有线段排序，其实就是从全局来考虑，这样问题会化简很多，判断最大最小面积三角形，以及四边形面积存在性也用到过这个思想。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define eps 1e-8
const int N = 300+9;
struct Point{
    ll x,y;
    int id;
    Point operator - (const Point& b)const{
        return (Point){x-b.x,y-b.y};
    }
    double ang(){return atan2(y,x);}
    ll cross(Point b){
        return x*b.y - b.x*y;
    }
}p[N];
ll dp[N][N][7];
struct Seg{
    Point s,t;
    bool operator < (const Seg& b)const{
        double anga = (t-s).ang() , angb = (b.t-b.s).ang();
        if( fabs(anga - angb) > eps) return anga < angb;
        return (t-s).cross(b.t-b.s) >0;
    }
}seg[N*N];
int main(){
    int n;
    int cnt = 0;
    scanf("%d",&n);
    for(int i = 1;i<=n;++i){
        scanf("%lld %lld",&p[i].x,&p[i].y);
        p[i].id = i;
    }
    for(int i = 1;i<=n;++i){
        for(int j = i + 1;j<=n;++j){
            seg[++cnt] = (Seg){p[i],p[j]};
            seg[++cnt] = (Seg){p[j],p[i]};
        }
    }
    sort(seg+1,seg+1+cnt);
    for(int i = 1;i<=cnt;++i){
        int tid = seg[i].t.id , sid = seg[i].s.id;
        dp[sid][tid][1] += 1;
        for(int j = 1;j<=n;++j){
            for(int k = 2;k<=5;++k){
                dp[sid][j][k] += dp[tid][j][k-1];
            }
        }
    }
    ll ans = 0;
    for(int i = 1;i<=n;++i) ans += dp[i][i][5];
    printf("%lld",ans);
}

接下来几天先放放计几，打算训练一下图论以及cf题，提高一下个人能力。

（upd ： 还是打算把cf2900以下的，题号500+的刷一波吧）

 

2020.4.24 第十三题：codeforces598F

题意：给你一个1000个点的简单多边形，给你100条直线，问你每条直线和多边形相交的部分的长度。

 

 edu1 的 F 题。。。。。

emm 思路很简单，就是对于每条直线，暴力求和简单多边形的交点，然后再统计，就是O（nm）的。 但是有一个很烦的问题就是，你怎么统计。

很容易想到射线法判断点是否在凸包里面的方法，就是每一个交点，我们就相当于 凸包内/ 凸包外 的一个状态转化，所以很容易求出来。但是有个问题就是我射线法只是判断点是不是在凸包内，所以我遇到平行线段就直接不管。但是这里不行啊！那如果平行的直接加进答案？不行！会重复，思考了一个晚上，假了一个晚上，早上起来实在没想到别的了，于是乎打了一个扫描线居然就过了。。

总体做法：先对图旋转，问题变成多边形和x轴相交线段，然后我们开一个 add 数组记录添加的线段，对于x轴上的线段直接丢进add，其他的情况也丢进add，最后add进行扫描线，这样就不会重复了。

#include<bits/stdc++.h>
using namespace std;
#define eps 1e-8
const int N = 1000+9;
struct Point{
    double x,y;
    Point operator - (const Point& b)const{
        return (Point){x-b.x,y-b.y};
    }
    Point operator * (const double& b)const{
        return (Point){x*b,y*b};
    }
    Point operator / (const double& b)const{
        return (Point){x/b,y/b};
    }
    Point turn(const double& k){
        return (Point){ x*cos(k)-y*sin(k),x*sin(k)+y*cos(k)};
    }
    double cross(Point a,Point b){
        return (a.x-x) * (b.y-y) - (b.x-x)*(a.y - y);
    }
    bool operator < (const Point& b)const{
        if( fabs(x-b.x) < eps ) return y < b.y;
        return x < b.x;
    }
    
}p[N],tp[N];
double X[N*3],Xadd[N*3];
// struct Node{
//     int num;
//     double x1,x2;
//     bool operator < (const Node& b)const{
//         return x1 < b.x1;
//     }
// };
int sgn(double x){
    if( fabs(x) < eps ) return 0;
    if( x < 0) return -1;
    return 1;
}
double dis(Point a,Point b){
    return sqrt((a.x - b.x)*(a.x-b.x) + (a.y-b.y)*(a.y-b.y));
}
bool insert(Point a,Point b,Point c,Point d){
    // cerr<<c.x<<" "<<c.y<<" "<<d.x<<" "<<d.y<<" "<<sgn(a.cross(b,d))<<" "<<a.cross(b,d)<<"!!"<<endl;
    // if( sgn( a.cross(b,d)) == 0 ) return 1;
    return sgn( a.cross(b,c) ) * sgn( a.cross(b,d) ) < 0;
}
Point LineCross(Point a,Point b,Point c,Point d){
    double u = a.cross(b,c), v = b.cross(a,d);
    return (Point){ (c.x*v + d.x*u)/(u+v) , (c.y*v + d.y*u)/(u+v) };
}
int n; 
void init(){
    int cnt = 0;
    for(int i = 1;i<=n+1;++i){
        if( cnt>=2 && sgn(p[i].cross(tp[cnt],tp[cnt-1])) == 0 ) --cnt;
        tp[++cnt] = p[i];
    }
    for(int i = 1;i<=cnt;++i) p[i] = tp[i];
    n = cnt-1;
}
void solve(Point s,Point t){
    double deta = atan2(t.y-s.y,t.x-s.x);
    for(int i = 1;i<=n+1;++i){
        tp[i] = (p[i]-s).turn(-deta);
        // cerr<<i<<" "<<tp[i].x<<" "<<tp[i].y<<endl;
    }
    t = (Point){-1000000,0};
    s = (Point){1000000,0};
    int cnt = 0;
    // vector<Node> vec;
    vector< pair<double,double> > add;
    vector<double> tem;
    for(int i = 1;i<=n;++i){
        Point a = tp[i] , b = tp[i+1];
        if( fabs(a.y) < eps && fabs(b.y)<eps ){
            add.push_back({min(a.x,b.x) , max(a.x,b.x)});
            X[++cnt] = a.x; X[++cnt] = b.x;
            continue;
        }
        if( a.y > b.y + eps ) swap(a,b);
        if( fabs(b.y) < eps || ( fabs(a.y) > eps && insert(s,t,a,b) ) ){
            Point pt = LineCross(s,t,a,b);
            // cerr<<i<<" "<<tem.x<<" "<<tem.y<<endl;
            // tem.x1 = pt.x; tem.num = 1;
            // vec.push_back(tem);
            tem.push_back(pt.x);
            X[++cnt] = pt.x;
        }
    }
    double ans = 0;
    sort(X+1,X+1+cnt);
    cnt = unique(X+1,X+1+cnt) - X - 1;
    sort(tem.begin(),tem.end());
    for(int i = 0;i<tem.size();i+=2)  add.push_back({tem[i],tem[i+1]});
    for(int i = 1;i<=cnt;++i) Xadd[i] = 0;
    for(auto it : add){
        int pl = lower_bound(X+1,X+1+cnt,it.first) - X;
        int pr = lower_bound(X+1,X+1+cnt,it.second) - X;
        Xadd[pl] += 1; Xadd[ pr ] -= 1;
    }
    int num = 0;
    for(int i = 1;i<cnt;++i){
        num += Xadd[i];
        if( num ) ans += X[i+1] - X[i];
    }
    printf("%.15f\n",ans);
}
int main(){
    int m;
    scanf("%d",&n);
    scanf("%d",&m);
    for(int i = 1;i<=n;++i) scanf("%lf %lf",&p[i].x,&p[i].y);
    p[n+1] = p[1];
    init();
    for(int i = 1;i<=m;++i){
        Point a,b; scanf("%lf %lf %lf %lf",&a.x,&a.y,&b.x,&b.y);
        solve(a,b);
    }
    return 0;
}
/*
4 1
0 0
0 1
1 1
1 0
1 1 0 0
*/

 正解：多边形线段看作有向线段，和直线向量所成正向的线段+，反向线段 - 。 其中规范相交的权值是2，交在端点上权值是1 ，和直线平行的不管。 然后再 扫描线（和我的差不多，因为交正向相当于进入多边形，交反向相当于离开多边形，处理端点，射线法是只管高点，这里是让交点是端点的权值 = 1 ，因为不规范相交不会影响，所以权值设小点就没影响了。

//
//  Created by TaoSama on 2016-01-19
//  Copyright (c) 2015 TaoSama. All rights reserved.
//
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <map>
#include <queue>
#include <string>
#include <set>
#include <vector>

using namespace std;
#define pr(x) cout << #x << " = " << x << "  "
#define prln(x) cout << #x << " = " << x << endl
const int N = 1e5 + 10, INF = 0x3f3f3f3f, MOD = 1e9 + 7;

#define double long double
const double EPS = 1e-8;

int sgn(double x) {
    return x < -EPS ? -1 : x > EPS;
}

struct Point {
    double x, y;
    Point() {}
    Point(double x, double y): x(x), y(y) {}
    void read() {cin >> x >> y;}
    Point operator-(const Point& p) {
        return Point(x - p.x, y - p.y);
    }
    double operator*(const Point& p) {
        return x * p.x + y * p.y;
    }
    double operator^(const Point& p) {
        return x * p.y - y * p.x;
    }
    double length() {return hypotl(x, y);}
} poly[N];

using Vec = Point;

double getIntersection(Point p, Vec v, Point q, Vec w) {
    return (w ^ (p - q)) / (v ^ w);
}

int n, q;

double gao(Point p, Vec v) {
    double ret = 0;
    vector<pair<double, int> > pos;
    for(int i = 1; i <= n; ++i) {
        int s1 = sgn(v ^ (poly[i] - p));
        int s2 = sgn(v ^ (poly[i + 1] - p));
        if(s1 == s2) continue; //collinear or no intersection
        double o = getIntersection(p, v, poly[i], poly[i + 1] - poly[i]);
        if(s1 > s2) pos.push_back({o, s1 && s2 ? 2 : 1});
        else pos.push_back({o, s1 && s2 ? -2 : -1});
    }
    sort(pos.begin(), pos.end());
    int flag = 0;
    for(int i = 0; i + 1 < pos.size(); ++i) {
        flag += pos[i].second;
        if(flag) ret += pos[i + 1].first - pos[i].first;
    }
    return ret * v.length();
}

int main() {
#ifdef LOCAL
    freopen("C:\\Users\\TaoSama\\Desktop\\in.txt", "r", stdin);
//  freopen("C:\\Users\\TaoSama\\Desktop\\out.txt","w",stdout);
#endif
    ios_base::sync_with_stdio(0);

    cin >> n >> q;
    for(int i = 1; i <= n; ++i) poly[i].read();
    poly[n + 1] = poly[1];
    while(q--) {
        Point A, B;
        A.read(); B.read();
        cout << fixed << setprecision(20) << gao(A, B - A) << '\n';
    }
    return 0;
}

 

2020.4.25 第十四题：codeforces611G

就是类似于旋转卡壳的一道题，记住多个点和一个点的叉积的和是可以变成 多个点的和的虚点 和 这个点的叉积，然后就是一个前缀和瞎搞就好了。这题很容易爆ll，然后注意面积不能取模。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 5e5+8;
const ll modd = 1e9+7;
struct Point{
    ll x,y;
    Point operator - (const Point& b)const{
        return (Point){x-b.x,y-b.y};
    }
}p[N*2],all,tp[N*2];
ll cross(Point a,Point b){
    return a.x*b.y - b.x*a.y;
}
ll a[N*2],sum[N*2],ssum[N*2];
int n; 
int main(){
    scanf("%d",&n);
    for(int i = 1;i<=n;++i) scanf("%lld %lld",&p[i].x,&p[i].y);
    reverse(p+1,p+1+n);
    
    for(int i = 1;i<=n;++i) p[i+n] = p[i];
    for(int i = 1;i<2*n;++i) a[i] = cross(p[i],p[i+1]) % modd;
    for(int i = 1;i<2*n;++i) sum[i] = (sum[i-1] + a[i])%modd;
    for(int i = 1;i<2*n;++i) ssum[i] = (ssum[i-1] + sum[i])%modd;
    
    ll tot = 0 , ans = 0;
    all.x = 0 , all.y = 0;
    for(int i = 1;i<=n;++i) tot += cross(p[i],p[i+1]);
    double dtot = 1.0 * tot;
    ll now = cross(p[1],p[2]);
    ll cnt =0;
    for(int l = 1,r=2;l<=n;++l){
        
        while( now + cross(p[r],p[r+1]) + cross(p[r+1],p[l]) < dtot/2 ){
            now += cross(p[r],p[r+1]);
            ++r;
            all.x = (all.x + p[r].x + modd )%modd;
            all.y = (all.y + p[r].y + modd )%modd;
        }
        ll tem = ( (ssum[r-1] - ssum[l] - (r-l-1)*sum[l-1]%modd + modd)%modd + cross(all,p[l])%modd ) % modd;
        ans = (ans + tem) % modd;
        all.x = (all.x - p[l+2].x + modd) % modd;
        all.y = (all.y - p[l+2].y + modd) % modd;
        now -= cross(p[l],p[l+1]);
        cnt += r-l-1;
    }
    tot = tot % modd;
    ans = (cnt %modd * tot % modd - 2 * ans%modd + modd) % modd;
    printf("%lld",ans);
    return 0;
}

 

2020.4.26 第十五题：codeforces958E3

分治构造题。做法：对于分治的点，找到左下角的点，扫描线找到左边的百点和黑点相同就break出来，继续分分治。 首先，假如有解，我一定可以根据这个做法构造出来的。因为假如说左边黑点链接右面百点，那么我们肯定可以重新构造来使得左边白点等于黑点，这个画画图就好了。。。。那么我这样做能找到最终解么？肯定的，因为每次这样操作一定是保证了线段不交，然后每一次操作都是一定保证线段不交，最后答案就肯定是线段不交

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e4+9;
struct Point{
    int col,id;
    int x,y;
    bool operator < (const Point& b){
        if( x == b.x ) return y < b.y;
        return x < b.x;
    }
}p0,p[N*2];
int cross(Point a,Point b,Point c){
    return (b.x-a.x)*(c.y-a.y) - (c.x-a.x)*(b.y-a.y);
}
bool cmpang(Point a,Point b){
    return cross(p0,a,b) > 0;
}
int ans[N];
void solve(int L,int R){
    int c = L;
    for(int i = L;i<=R;++i) if(p[i]<p[c]) c = i;
    swap(p[c],p[L]);
    p0 = p[L];
    sort(p+L+1,p+R+1,cmpang);
    int a1 = 0, a0 = 0;
    int k = 1000000;
    int mid = (L+R)>>1;
    // cerr<<L<<" "<<R<<" LR"<<endl;
    for(int i = L+1;i<= R ;++i){
        if( a1 == a0 && p[i].col != p0.col){
                k = i;
                break;
            // cerr<<"!!!"<<p0.id<<" "<<p[i].id<<"!!"<<endl;
            // break;
        }
        if(p[i].col) ++a1;
        else ++a0;
    }
    if(p0.col) ans[p[k].id] = p0.id;
    else ans[p0.id] = p[k].id;
    // cerr<<p0.x<<" "<<p0.y<<" "<<p[k].x<<" "<<p[k].y<<" !"<<endl;
    // swap(p[L],p[k-1]);
    if(L+1<k-1) solve(L+1,k-1);
    if(k+1 < R) solve(k+1,R);
}
inline int read() {
    char ch = getchar(); int x = 0, f = 1;
    while(ch < '0' || ch > '9') {
        if(ch == '-') f = -1;
        ch = getchar();
    } while('0' <= ch && ch <= '9') {
        x = x * 10 + ch - '0';
        ch = getchar();
    } return x * f;
}
int main(){
    
    int n = read();
    for(int i = 1;i<=n;++i){
        p[i].x = read();
        p[i].y = read();
        p[i].col = 0; p[i].id = i;
    }
    for(int i = 1;i<=n;++i){
        p[i+n].x = read();
        p[i+n].y = read();
        p[i+n].col = 1; p[i+n].id = i;
    }
    solve(1,2*n);
    for(int i = 1;i<=n;++i) cout<<ans[i]<<"\n";
}

 

2020.5.6 第十六题：codeforces962G

突然发现鸽了好多天了。最近忙着作业还有其他东西，计几就停了一下。

题意：给你一个只有水平和垂直线段的简单多边形，内部染成黑色，然后给你一个矩形，问矩形内有多少个黑色区域。

做法：这题假了好多次，然后卡了一下午总算过了。其实计几有个常用的套路就是线段有向，以逆时针为方向。那么顺着这个思路想，我们可以对原来的图形建立有向线段的图。多边形和矩形交的线段在图内。矩形边上的点也在图内。然后一个黑色区域是可以从一个点dfs回自身的。所以建完图之后跑一遍dfs即可。

#include<bits/stdc++.h>
using namespace std;
const int N = 15000+9;
typedef long long ll;
struct Point{
    int x,y;
    Point operator - (const Point& b)const{
        return (Point){x-b.x,y-b.y};
    }
}p[N],rec[7],Gp[N];
bool vis[N*5];
vector< pair<int,int> > edge_pt[5];
map<pair<int,int> , int > mp;
vector<int> G[N];
// int cross(Point a,Point b,Point c){
//     return (b.x-a.x)*(c.y-b.y) - (c.x-a.x) * (a.y-b.y);
// }
// int dot(Point a,Point b,Point c){
//     return (b.x-a.x)*(c.x-a.x) + (b.y-a.y)*(c.y-a.y);
// }
// bool onSeg(Point a,Point s,Point e){
//     return cross(a,s,e)==0 && dot(a,s,e) <= 0 ;
// }
int n;
int cnt = 0;
bool judge(){
    double xx = (rec[1].x + rec[3].x) * 0.5;
    double yy = (rec[1].y + rec[3].y) * 0.5;
    int cnt = 0;
    // for(int i = 1;i<=4;++i){
    //     if( onSeg(,rec[i],rec[i+1])) return 1;
    // }
    for(int i = 1;i<=n;++i){
        if( p[i].y == p[i+1].y) continue;
        if( p[i].x < xx) continue;
        int mi = min(p[i].y,p[i+1].y) , mx = max(p[i].y,p[i+1].y);
        // cerr<<yy<<" "<<mi<<" "<<mx<<" !!"<<endl;
        if( yy <= mi || yy > mx) continue;
        ++cnt;
    }
    if( cnt&1 ) return 1;
    return cnt&1;
}
void add(int xa,int ya,int xb,int yb){
    if( !mp[{xa,ya}] ) mp[{xa,ya}] = ++cnt;
    if( !mp[{xb,yb}] ) mp[{xb,yb}] = ++cnt;
    int aid = mp[{xa,ya}], bid = mp[{xb,yb}];
    G[aid].push_back(bid);
    if( xa == rec[1].x ) edge_pt[1].push_back({ya,aid});
    if( xa == rec[3].x ) edge_pt[3].push_back({ya,aid});
    if( ya == rec[2].y ) edge_pt[2].push_back({xa,aid});
    if( ya == rec[4].y ) edge_pt[4].push_back({xa,aid});
    if( xb == rec[1].x ) edge_pt[1].push_back({yb,bid});
    if( xb == rec[3].x ) edge_pt[3].push_back({yb,bid});
    if( yb == rec[2].y ) edge_pt[2].push_back({xb,bid});
    if( yb == rec[4].y ) edge_pt[4].push_back({xb,bid});
}
void build_G(){
    for(int i = 1;i<=n;++i){
        if( p[i].x == p[i+1].x){
            // cerr<<i<<" "<<p[i].x<<" "<<p[i].y<<p[i+1].x<<" "<<p[i+1].y<<rec[1].x<<" "<<rec[3].x<<" !!!"<<endl;
            if( p[i].x <= rec[1].x || p[i].x >= rec[3].x ) continue;
            bool up = (p[i].y < p[i+1].y);
            int mx = max(p[i].y,p[i+1].y) , mi = min(p[i].y,p[i+1].y);
            mx = min(mx,rec[1].y) ; mi = max(mi,rec[2].y);
            if( mi < mx){
                // cerr<<i<<" "<<mi<<" "<<mx<<"miomx"<<endl;
                if(up) add(p[i].x,mi,p[i].x,mx);
                else add(p[i].x,mx,p[i].x,mi);
            }
        }
        else{
            if( p[i].y >= rec[1].y || p[i].y <= rec[3].y ) continue;
            bool ri = (p[i].x < p[i+1].x);
            int mx = max(p[i].x,p[i+1].x) , mi = min(p[i].x,p[i+1].x);
            mx = min(mx,rec[3].x) ; mi = max(mi,rec[1].x);
            if( mi < mx){
                if(ri) add(mi,p[i].y,mx,p[i].y);
                else add(mx,p[i].y,mi,p[i].y);
            }
        }
    }
    // cerr<<cnt<<" "<<cnt<<"!"<<endl;
    if( cnt == 0 ){
        if(judge()) printf("1");
        else printf("0");
        exit(0);
    }
    for(int i = 1;i<=4;++i){
        if( mp[{rec[i].x,rec[i].y}]) continue;
        mp[{rec[i].x,rec[i].y}] = ++cnt;
        int x = rec[i].x , y = rec[i].y;
        if( x == rec[1].x ) edge_pt[1].push_back({y,cnt});
        if( x == rec[3].x ) edge_pt[3].push_back({y,cnt});
        if( y == rec[2].y ) edge_pt[2].push_back({x,cnt});
        if( y == rec[4].y ) edge_pt[4].push_back({x,cnt});
    }
    for(int i = 1;i<=4;++i){
        sort(edge_pt[i].begin(),edge_pt[i].end());
        if( i == 1 || i == 4) reverse(edge_pt[i].begin(),edge_pt[i].end());
        if( mp[{rec[i].x,rec[i].y}] == 0) mp[{rec[i].x,rec[i].y}] = ++cnt;
        if( mp[{rec[i+1].x,rec[i+1].y}] == 0) mp[{rec[i+1].x,rec[i+1].y}] = ++cnt;
        int s = mp[{rec[i].x,rec[i].y}] , e = mp[{rec[i+1].x,rec[i+1].y}];
        for(int j = 0;j<edge_pt[i].size();++j){
            if( j == edge_pt[i].size() - 1 && edge_pt[i][j].second != e) G[edge_pt[i][j].second].push_back(e);
            if( j == 0 && edge_pt[i][j].second != s) G[s].push_back(edge_pt[i][j].second);
            if( j!= edge_pt[i].size()-1) G[edge_pt[i][j].second].push_back(edge_pt[i][j+1].second);
        }
    }
}
bool dfs(int u,int fa){
    // cerr<<u<<" dfsu"<<endl;
    for(auto v : G[u]){
        // cerr<<v<<" v"<<endl;
        if(v == fa){
            // cerr<<v<<" findv"<<endl;
            return 1;
        }
        if( vis[v] == 0){
            vis[v] = 1;
            if( dfs(v,fa) ) return 1;
        }
    }
    return 0;
}
int main(){
    int x1,y1,x2,y2;
    scanf("%d %d %d %d",&x1,&y1,&x2,&y2);
    rec[1] = (Point){x1,y1};
    rec[2] = (Point){x1,y2};
    rec[3] = (Point){x2,y2};
    rec[4] = (Point){x2,y1};
    rec[5] = rec[1];
    scanf("%d",&n);
    for(int i = 1;i<=n;++i) scanf("%d %d",&p[i].x,&p[i].y);
    p[n+1] = p[1];

    bool cont = 1;
    for(int i = 1;i<=n;++i){
        if( p[i].x < rec[1].x || p[i].x > rec[3].x || p[i].y < rec[2].y || p[i].y > rec[4].y) cont = 0;
    }
    if( cont){
        printf("1");
        return 0;
    }
    build_G();
    // for(auto it : mp){
    //     cerr<<it.first.first<<" "<<it.first.second<<" "<<it.second<<"!"<<endl;
    // }
    int ans = 0;
    for(int i = 1;i<=cnt;++i){
        if(!vis[i]){
            vis[i] = 1;
            if(dfs(i,i)) ++ans;
        }
    }
    printf("%d",ans);
}
/*
0 5 10 0
8
0 0
2 0
2 8
8 8 
8 0
10 0
10 10
0 10
*/

 5.7（补）：首先具体说说做法：就是逆时针建图，包括矩形。然后dfs的意思是，找一个点，如果能dfs回自身，说明是一个合法区域，然后不会走过经过的点。然后今天早上的时候发现做法有点假，就是假如我先从矩形顶点出发，绕矩形一圈，那么剩下的那些合法的，靠着矩形边的区域就统计不到。再比如，假如我从一个合法区域开始dfs，假如我先走矩形边，走到另一个区域，那么我自身的区域就统计不到，而且我走到的另一个区域因为打了vis标记，所以也统计不到。

然后我想了一个下午怎么修改，但是还是没有解决。然后我突然发现，其实我原来的做法的一个小细节能够把这些繁琐的问题解决，就是我建点是先建立多边形上的，再建立矩形上的，边也是一样。所以我们在遍历起点的时候，会优先遍历多边形上的，第一个问题解决了。第二个问题？？一样，我们dfs优先遍历多边形上的边，也就保证我先走自身的那个区域，然后我dfs到自身就直接return，所以链接两个区域的矩形边不会被遍历到。

今天虽然没做新题，但是巩固了昨天的题。从觉得自己昨天就是个傻逼，写出这垃圾算法，怀疑cf数据，想明白之后才发现昨天自己居然写了一个神仙算法自己都没发现，哈哈哈哈哈。

 

2020.5.8 第十七题：codeforces887E

这题其实挺简单的，就是对于每个圆，二分求出不合法区域，全部求出来之后跑一遍扫描线就好了。

#include<bits/stdc++.h>
using namespace std;
#define inf 1e12+9
#define eps 1e-7
struct Point{
    double x,y,r;
    Point operator + (const Point& b)const{
        return (Point){x+b.x,y+b.y};
    }
    Point operator - (const Point& b)const{
        return (Point){x-b.x,y-b.y};
    }
    Point operator * (const double& b)const{
        return (Point){x*b,y*b};
    }
    Point operator / (const double& b)const{
        return (Point){x/b,y/b};
    }
    double len(){ return sqrt(x*x+y*y); }
}p0,p1,p2,v;
double cross(Point a,Point b,Point c){
    return (b.x-a.x)*(c.y-a.y) - (c.x-a.x)*(b.y-a.y);
}
vector< pair<double,int> > vec;
void add(Point tem){
    double L = -inf , R = inf;
    double a1,a2;
    if(cross(p1,p2,tem) > eps ) swap(L,R);
    for(int k = 1;k<=100;++k){
    // while(fabs(R-L) > eps){
        double m = (L+R)/2;
        Point pm = p0 + v * m;
        double len = (pm-p1).len();
        double dis = (pm-tem).len();
        // cerr<<L<<" "<<R<<" "<<m<<" "<<dis<<" "<<tem.r<<" "<<len<<" !!"<<endl;
        // cerr<<pm.x<<" "<<pm.y<<" xy"<<endl;
        if( fabs(dis - tem.r) < len ) L = m;
        else R = m;
    }
    // cerr<<L<<" !"<<endl;
    a1 = L;

    L = -inf , R = inf;
    if(cross(p1,p2,tem) > eps ) swap(L,R);
    for(int k = 1;k<=100;++k){
    // while( fabs(R-L) > eps){
        double m = (L+R)/2;
        Point pm = p0 + v * m;
        double len = (pm-p1).len();
        double dis = (pm-tem).len();
        if( fabs(dis + tem.r) < len ) L = m;
        else R = m;
    }
    // cerr<<L<<" !"<<endl;
    a2 = R;
    if( a1 > a2 ) swap(a1,a2);
    // cerr<<a1<<" "<<a2<<" a12"<<endl;
    vec.push_back({a1,1});
    vec.push_back({a2,-1});
}
void solve(){
    vec.push_back({0,0});
    sort(vec.begin(),vec.end());
    double ans = inf;
    int cnt = 0;
    for(int i = 0;i<vec.size();++i){
        // cerr<<vec[i].first<<" "<<vec[i].second<<" "<<cnt<<" cnmt"<<endl;
        if(cnt == 0 ) ans = min(ans,fabs(vec[i].first) );
        cnt += vec[i].second;
        if(cnt == 0 ) ans = min(ans,fabs(vec[i].first) );
    }
    // cerr<<ans<<" !"<<endl;
    double len = (p2-p1).len() * 0.5;
    ans = sqrt(ans*ans + len*len);
    printf("%.10f",ans);
    return;
}
int main(){
    scanf("%lf %lf %lf %lf",&p1.x,&p1.y,&p2.x,&p2.y);
    p0 = (p1+p2)*0.5;
    v.x = -(p2-p1).y; v.y = (p2-p1).x;
    v = v / v.len();
    int n; scanf("%d",&n);
    for(int i = 1;i<=n;++i){
        Point tem; scanf("%lf %lf %lf",&tem.x,&tem.y,&tem.r);
        add(tem);
    }
    solve();
}
/*
0 0 10 0 
1
5 2 1
*/

 

2020.5.10 第十八题：codeforces575E

给你若干点，在这些点中选三个点，使得外接圆包含所有点，同时满足半径最大。

先求凸包，外接圆最大，肯定三个点接近比较好，所以枚举凸包连续的三个点即可。然后因为最小原覆盖的定理说明肯定能选择三个点满足外接圆包含所有点，所以肯定找得到。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll lim = 1e5;
const int N = 8e5+9;
struct Point{
    ll x,y;
    bool operator < (const Point& b)const{
        if( x == b.x ) return y < b.y;
        return x < b.x;
    }
}p[N],ch[N],ans[5];
int cnt = 0;
ll cross(Point a,Point b,Point c){
    return (b.x-a.x) * (c.y - a.y) - (c.x - a.x) * (b.y-a.y);
}
double dist(Point a,Point b){
    return sqrt( 1.0*(a.x - b.x)*(a.x - b.x) + (a.y - b.y)*(a.y-b.y) );
}
void add(Point tem,ll v){
    if(tem.x - v >= 0 ) p[cnt++] = (Point){tem.x - v,tem.y};
    else{
        ll deta = v - tem.x;
        ll ya = max((ll)0,tem.y-deta);
        ll yb = min(lim,tem.y + deta);
        p[cnt++] = (Point){(ll)0,ya};
        p[cnt++] = (Point){(ll)0,yb};
    }

    if(tem.x + v <= lim ) p[cnt++] = (Point){tem.x + v,tem.y};
    else{
        ll deta = v + tem.x - lim;
        ll ya = max((ll)0,tem.y-deta);
        ll yb = min(lim,tem.y + deta);
        p[cnt++] = (Point){lim,ya};
        p[cnt++] = (Point){lim,yb};
    }

    if(tem.y - v >= 0 ) p[cnt++] = (Point){tem.x,tem.y-v};
    else{ 
        ll deta = v - tem.y;
        ll xa = max((ll)0,tem.x-deta);
        ll xb = min(lim,tem.x + deta);
        p[cnt++] = (Point){xa,(ll)0};
        p[cnt++] = (Point){xb,(ll)0};
    }

    if(tem.y + v <= lim ) p[cnt++] = (Point){tem.x,tem.y+v};
    else{ 
        ll deta = v + tem.y - lim;
        ll xa = max((ll)0,tem.x-deta);
        ll xb = min(lim,tem.x + deta);
        p[cnt++] = (Point){xa,lim};
        p[cnt++] = (Point){xb,lim};
    }
}
int Andrew(){
    sort(p,p+cnt);
    int m = 0;
    for(int i = 0;i<cnt;++i){
        while( m > 1 && cross( ch[m-2] , p[i], ch[m-1]) >= 0 ) --m;
        ch[m++] = p[i];
    }
    int k = m;
    for(int i = cnt-2;i>=0;--i){
        while( m > k && cross(ch[m-2] , p[i],ch[m-1]) >= 0 ) --m;
        ch[m++] = p[i];
    }
    if(cnt > 1) -- m;
    return m;
}
double CirR(Point a,Point b,Point c){
    double sth = 1.0 * abs( cross(a,b,c) )/( dist(a,b) * dist(a,c) ) ;
    return dist(b,c) / sth;
}
int main(){
    int n; scanf("%d",&n);
    for(int i = 1;i<=n;++i){
        ll v;
        Point tem; scanf("%lld %lld %lld",&tem.x,&tem.y,&v);
        add(tem,v);
    }
    int m = Andrew();
    double res = 0;
    ch[m] = ch[0]; ch[m+1] = ch[1];
    for(int i = 0;i<m;++i){
        if( CirR(ch[i],ch[i+1],ch[i+2]) > res){
            res = CirR(ch[i],ch[i+1],ch[i+2]);
            ans[0] = ch[i];
            ans[1] = ch[i+1];
            ans[2] = ch[i+2];
        }
    }
    for(int i = 0;i<3;++i) printf("%lld %lld\n",ans[i].x,ans[i].y);
    return 0;
}

 

2020.5.11 第十九题：codeforces717I  Cowboy Beblop at his computer

题意：三维空间给你两个平面环，问两个平面环是否“well-connect"(定义：不能平移，缩小旋转使得两个环分开），其实就是两个橡皮筋是否套起来。

做法： 这是我第四道三维计几。因为一个小细节wa了一发。思路挺好想的：题意已经告诉我们，只需要统计b环的线段中，从不同方向穿过a环的数量，比较数量是否相同即可。然后我们要做的就是把交点全求出来，然后两平面相交是直线，所以点都在一个直线上，然后我们求出直线和a环的交点，用排个序，用射线法就可以处理出点是否在环a内。然后统计就好了。

细节（wa点）：b环线段满足什么条件才统计进入答案？统计起点不统计终点是不行的，用射线法常用方法就是统计高出线段端点，不统计线段低点即可。

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+9;
#define eps 1e-8
struct Point{
    double x,y,z;
    int ty;
    Point operator - (const Point& b)const{
        return (Point){x-b.x,y-b.y,z-b.z};
    }
    Point operator + (const Point& b)const{
        return (Point){x+b.x,y+b.y,z+b.z};
    }
    double len(){
        return sqrt(x*x+y*y+z*z);
    }
    Point operator * (const double& b)const{
        return (Point){x*b,y*b,z*b};
    }
}pn[N],pm[N],hn,hm,Linep[N*2];
pair<double,int> num[N*2];
int n,m,cnt;
double dot(Point a,Point b){
    return a.x*b.x + a.y * b.y + a.z*b.z;
}
Point cross(Point a,Point b){
    return (Point){a.y*b.z-a.z*b.y,a.z*b.x-a.x*b.z,a.x*b.y-a.y*b.x};
}
//直线和平面交点
Point LinePlaneIntersection(Point p1,Point p2,Point p0,Point n){
    Point v = p2 - p1;
    double t = (dot(n,p0-p1) / dot(n,p2-p1));
    return p1 + v*t;
}
Point LineCross(Point a,Point b,Point c,Point d){
    Point n = cross(b-a,d-c);
    n = d+n;
    Point f = cross(d-c,n-c);
    double t = dot(f,c-a)/dot(f,b-a);
    Point res = a + (b-a)*t;
    return res;
}
void solve(){
    cnt = 0;
    for(int i = 1;i<=n;++i){
        double nf = dot(hm,pn[i] - pm[1]);
        double nt = dot(hm,pn[i+1] - pm[1]);
        bool cro = 0;
        if( nf * nt < -eps ) cro = 1;
        else if( nf * nt < eps ){
            if(nf < -eps || nt < -eps ) cro = 1;
        }
        if( cro ){
            int tp;
            if(nf < -eps ) tp = 1;
            else tp = -1;
            Linep[++cnt] = LinePlaneIntersection(pn[i],pn[i+1],pm[1],hm);
            Linep[cnt].ty = tp;
        }
    }
    // cerr<<cnt<<"!"<<endl;
    if(cnt == 0 ){
        puts("NO");
        return;
    }
    Point lv = cross(hn,hm);
    for(int i = 1;i<=m;++i){
        Point mf = cross(lv,pm[i]-Linep[1]);
        Point mt = cross(lv,pm[i+1]-Linep[1]);
        bool cro = 0;
        if( dot(mf,mt) < -eps ) cro = 1;
        else if(dot(mf,mt) < eps){
            if(dot(hm,mf) > eps || dot(hm,mt) > eps ) cro = 1;
        }
        if( cro ){
            Linep[++cnt] = LineCross(Linep[1],Linep[1]+lv,pm[i],pm[i+1]);
            Linep[cnt].ty = 0;
        }
    }
    // cerr<<cnt<<endl;
    for(int i = 1;i<=cnt;++i){
        num[i].first = dot(Linep[i] - Linep[1],lv);
        num[i].second = Linep[i].ty;
    }
    sort(num+1,num+1+cnt);
    int a0 = 0 , a1 = 0;
    int now = 0;
    for(int i = cnt;i>=1;--i){
        if(num[i].second == 0 ) ++now;
        else if(now&1){
            if(num[i].second == 1) ++a1;
            else ++a0;
        }
    }
    if(a1 == a0 ) puts("NO");
    else puts("YES");
}
int main(){
    scanf("%d",&n);
    for(int i = 1;i<=n;++i){
        int xx,yy,zz; scanf("%d %d %d",&xx,&yy,&zz);
        pn[i].x = xx; pn[i].y = yy; pn[i].z = zz;
    }
    scanf("%d",&m);
    for(int i = 1;i<=m;++i){
        int xx,yy,zz; scanf("%d %d %d",&xx,&yy,&zz);
        pm[i].x = xx; pm[i].y = yy; pm[i].z = zz;
    }
    pn[n+1] = pn[1]; pm[m+1] = pm[1];
    hn = cross(pn[2]-pn[1],pn[3]-pn[1]);
    hm = cross(pm[2]-pm[1],pm[3]-pm[1]);
    Point tem = cross(hn,hm);
    if(tem.len() < eps){
        puts("NO");
        return 0;
    }
    solve();
}

 

2020.5.17第二十题:http://codeforces.com/group/uVAsoW2Jkj/contest/280056/attachments

这是我们的训练赛的F题。最后我没过。。。主要是对最小圆覆盖没理解透彻以及一开始想歪思路了。

题意：给你300个黑白点，求出最小半径圆包含全部黑点而不包含白点。

一开始看到300，打算直接在黑点凸包上暴力枚举三个点。但其实这个做法很假，比如两个黑点连线，一个白点很靠近连线，那么我肯定不能够只考虑这两个黑点画圆，也就是我卡这个圆不仅仅要考虑黑点，白点也要卡。那么就是最小圆覆盖了。最小圆覆盖的本质就是卡圆的边界，枚举圆上的三个点，从而来卡这个圆。可以注意到，黑点不在当前圆，那么黑点肯定在答案圆弧上，白点如果在当前圆内，那么这个白点肯定也在圆弧上，然后就是板子了。注意的是圆弧上有黑白点，如果白色点的只有一段，那么圆是合法的，因为可以向一个方向轻微挪动，多于一段则不可。

哎。。。这几天没有练计几，就没有做出计几题了。然后一个学弟做出来了。难受。。。一开始光想着怎么暴力去了。

#include<bits/stdc++.h>
using namespace std;
const int N = 300+9;
const double inf = 1e20;
#define eps 1e-8
struct Point{
    double x,y;
    int ty;
    bool operator < (const Point& b)const{
        return x < b.x || (x==b.x && y < b.y);
    }
    Point operator - (const Point& b)const{
        return (Point){x-b.x,y-b.y};
    }
    Point rotate(){
        return (Point){-y,x};
    }
    int len(){
        return sqrt(x*x+y*y);
    }
}p[N],p0;
int n,na,nb;
struct Circle{
    Point o;
    double r;
};
int sgn(double x){
    if(fabs(x) < eps) return 0;
    if(x<0) return -1;
    return 1;
}
Point getmid(Point a,Point b){
    return (Point){(a.x+b.x)*0.5,(a.y+b.y)*0.5};
}
double cross(Point a,Point b,Point c){
    return (b.x-a.x)*(c.y-a.y) - (c.x-a.x)*(b.y-a.y);
}
double dis(Point a,Point b){
    return sqrt( (a.x-b.x)*(a.x-b.x) + (a.y-b.y)*(a.y-b.y) );
}
int Qua(Point a){
    if(a.x >= 0 && a.y >= 0 ) return 1;
    if( a.x <= 0 && a.y >= 0 ) return 2;
    if(a.x <= 0 && a.y <= 0 ) return 3;
    return 4;
}
bool cmp(Point a,Point b){
    Point ta = a - p0;
    Point tb = b - p0;
    if( Qua(ta) == Qua(tb) ){
        if(cross(p0,a,b) == 0 ) return a.len() < b.len();
        return cross(p0,a,b) > 0;
    }
    else return Qua(ta) < Qua(tb);
}
Point circlein(Point a,Point b,Point c){
    Point v1 = b-a , v2 = a-c;
    v1 = v1.rotate();  v2=v2.rotate();
    double p1x = (a.x+b.x)*0.5 , p1y = (a.y+b.y)*0.5;
    double p2x = (a.x+c.x)*0.5 , p2y = (a.y+c.y)*0.5;
    double ux = p1x - p2x , uy = p1y - p2y;
    double t = (v2.x * uy - ux*v2.y)/( 1.0*v1.x*v2.y - v2.x *v1.y);
    double ox = p1x + v1.x*t;
    double oy = p1y + v1.y*t;
    Point res = (Point){ox,oy};
    return res;
}
bool judge(Point a,Circle ans){
    if(a.ty){
        return dis(a,ans.o) > ans.r + eps;
    }
    return dis(a,ans.o) < ans.r - eps;
}
void solve(){
    if(na==0){
        puts("0");
        return;
    }
    random_shuffle(p+1,p+1+n);
    Circle ans = (Circle){p[1],0};
    for(int i = 2;i<=n;++i){
        if(judge(p[i],ans)){
            ans = (Circle){p[i],0};
            for(int j = 1;j<i;++j){
                if(judge(p[j],ans)){
                    ans.o = getmid(p[i],p[j]);
                    ans.r = dis(p[i],p[j])/2;
                    for(int k = 1;k<j;++k){
                        if(judge(p[k],ans)){
                            ans.o = circlein(p[i],p[j],p[k]);
                            ans.r = dis(p[i],ans.o);
                            cerr<<ans.o.x<<" "<<ans.o.y<<" "<<p[i].x<<" "<<p[i].y<<endl;
                            cerr<<ans.r<<" !!!"<<endl;
                        }
                    }
                }
            }
        }
    }
    if(isinf(ans.r) || isnan(ans.r)){
        puts("The Orcs are close");
        return;
    }
    vector<Point> vec;
    for(int i = 1;i<=n;++i){
        if(judge(p[i],ans)){
            puts("The Orcs are close");
            return;
        }
        if( sgn(dis(ans.o,p[i]) - ans.r) == 0 ) vec.push_back(p[i]);
    }
    p0 = ans.o;
    sort(vec.begin(),vec.end(),cmp);
    int has = 0;
    for(int i = 0;i<vec.size();){
        if(vec[i].ty == 1 ){
            ++i;
            continue;
        }
        ++has;
        int j = i;
        while(j+1<vec.size() && vec[j+1].ty == 0 )++j;
        i = j+1;
    }
    bool ok = 0;
    if(has<=1){
        ok = 1;
    }
    else{
        if(has>2) ok = 0;
        else{
            if(vec[0].ty == 0 && vec[vec.size()-1].ty == 0 ) ok = 1;
            else ok = 0;
        }
    }
    if(ok) printf("%.15f\n",ans.r);
    else puts("The Orcs are close");
}
#define gc getchar()
inline int read(int &x){
    char ch; while(!isdigit(ch = gc)) if(ch == '\n' || ch == EOF) return 0; x = ch ^ 48;
    while(isdigit(ch = gc)) x = x * 10 + (ch ^ 48); return 1;
}
int main(){
    char ch;
    while((ch = gc) != EOF){
        n = na = nb = 0;
        int tx,ty;
        while(read(tx)){
            ++n;
            p[n].x = tx;
            read(ty);
            p[n].y = ty;
            p[n].ty = 1;
            ++na;
        }
        while(read(tx)){
            ++n;
            ++nb;
            p[n].x = tx;
            read(ty);
            p[n].y = ty;
            p[n].ty = 0;
        }
        solve();
    }
}

 （补）：下面cf549题的启发，其实这题有个更简洁好懂的做法。就是黑点的凸包肯定有至少两个点，所以最终答案肯定是在凸包的两个点或三个点上面。然后我们枚举凸包上两个点，那么最终圆心会在这中垂线上，然后我们对于其余的黑点和白点，在这个中垂线上卡线段，最终卡出来的线段即更新答案。对于那种轻微偏移的情况，其实就是卡线段的开闭区间，不用判断白点是否一段。

这样看来这题真的就是傻逼题。当时以为共线就直接圆心终点，如果早点hack这个做法，然后顺着暴力思路往下想，就会想到枚举两点，第三点卡线段。啊，太菜了。

#include<bits/stdc++.h>
using namespace std;
const int N = 300+9;
const double inf = 1e18;
#define eps 1e-8
struct Point{
    double x,y;
    int ty;
    bool operator < (const Point& b)const{
        return x < b.x || (x==b.x && y < b.y);
    }
    Point operator - (const Point& b)const{
        return (Point){x-b.x,y-b.y};
    }
    Point operator + (const Point& b)const{
        return (Point){x+b.x,y+b.y};
    }
    Point operator * (const double& b)const{
        return (Point){x*b,y*b};
    }
}pa[N],pb[N],ch[N*2];
int na,nb,m;
struct Circle{
    Point o;
    double r;
};
int sgn(double x){
    if(fabs(x) < eps) return 0;
    if(x<0) return -1;
    return 1;
}
double cross(Point a,Point b){return a.x*b.y-b.x*a.y;}
double dot(Point a,Point b){return a.x*b.x + a.y*b.y;}
double len2(Point a){ return a.x*a.x + a.y*a.y;}
double len(Point a){return sqrt(len2(a));}
Point core(Point a,Point b,Point c){
    Point A=(Point){b.x-a.x,c.x-a.x}*2 , B = (Point){b.y-a.y,c.y-a.y}*2;
    Point C = (Point){ len2(b)-len2(a),len2(c)-len2(a) };
    return (Point){ cross(B,C)/cross(B,A),cross(A,C)/cross(A,B) };
}
int Andrew(){
    sort(pa,pa+na);
    int m = 0;
    for(int i = 0;i<na;++i){
        while( m > 1 && cross(pa[i] - ch[m-2],ch[m-1] - ch[m-2])>=0) --m;
        ch[m++] = pa[i];
    }
    int k = m;
    for(int i = na-2;i>=0;--i){
        while(m>k && cross(pa[i] - ch[m-2] ,ch[m-1] - ch[m-2])>=0) --m;
        ch[m++] = pa[i];
    }
    if(na>1) --m;
    return m;
}
double work(int f,int t){
    double l = -inf , r = inf;
    Point o = (ch[f] + ch[t])*0.5;
    for(int i = f+1;i<t;++i){
        Point c = core(ch[f],ch[t],ch[i]);
        double tem = len(c-o); 
        if( sgn(cross(ch[t] - ch[f] , c - ch[f])) > 0 ) tem = -tem;
        if( sgn(tem - l) > 0 ) l = tem;
    }
    for(int i = t+1;i<f+m;++i){
        Point c = core(ch[f],ch[t],ch[i]);
        double tem = len(c-o); 
        if( sgn(cross(ch[t] - ch[f] , c - ch[f])) > 0 ) tem = -tem;
        if( sgn(r - tem) > 0 ) r = tem;
    }
    if(r < l - eps) return inf;
    for(int i = 0;i<nb;++i){
        int fx = sgn(cross(ch[t] - ch[f],pb[i] - ch[f]));
        if(fx == 0){
            if( sgn( dot(ch[f] - pb[i] , ch[t] - pb[i]) ) < 0 ) return inf;
        }
        else{
            Point c = core(ch[f],ch[t],pb[i]);
            double tem = len(c-o);
            if( sgn(cross(ch[t] - ch[f] , c - ch[f])) > 0 ) tem = -tem;
            if( fx > 0 ){
                tem += 2*eps;
                if( sgn(tem - l) > 0 ) l = tem;
            }
            else{
                tem -= 2*eps;
                if( sgn(r - tem) > 0 ) r = tem;
            }
        }
    }
    if( r < l - eps ) return inf;
    double tem = len(ch[f]-ch[t])*0.5;
    if( r >-eps && l < eps) return tem;
    double mi = min(fabs(r),fabs(l));
    tem = sqrt(tem*tem + mi*mi);
    return tem;
}
void solve(){
    if(na <= 1){
        puts("0");
        return;
    }
    m = Andrew();
    for(int i = 0;i<m;++i) ch[i+m] = ch[i];
    double ans = inf;
    for(int i = 0;i<m;++i){
        for(int j = i+1;j<m;++j){
            ans = min(ans,work(i,j));
        }
    }
    if( ans == inf ) puts("The Orcs are close");
    else printf("%.12f\n",ans);
}
#define gc getchar()
inline int read(int &x){
    char ch; while(!isdigit(ch = gc)) if(ch == '\n' || ch == EOF) return 0; x = ch ^ 48;
    while(isdigit(ch = gc)) x = x * 10 + (ch ^ 48); return 1;
}
int main(){
    char ch;
    while((ch = gc) != EOF){
        int tx,ty;
        na = nb = 0;
        while(read(tx)){
            pa[na].x = tx;
            read(ty);
            pa[na].y = ty;
            ++na;
        }
        while(read(tx)){
            pb[nb].x = tx;
            read(ty);
            pb[nb].y = ty;
            ++nb;
        }
        solve();
    }
}

 

2020.5.19 第二十一题：codeforces549E

题意：给你10000黑白点，问是否有圆可以把黑白点严格分割开。

题解：这题用上一题的最小圆覆盖做法居然没过？？？？震惊。。。

这题做法：https://blog.csdn.net/zava_1087/article/details/46447069

就是二维划为三维，然后卡三维的棱变成卡二维的棱。

#include<bits/stdc++.h>
using namespace std;
#define eps 1e-10
#define inf 1e16
const int N = 1e4+9;
struct Point{
    double x,y;
    Point operator - (const Point& b)const{
        return (Point){x-b.x,y-b.y};
    }
    Point operator + (const Point& b)const{
        return (Point){x+b.x,y+b.y};
    }
    Point operator* (const double& b)const{
        return (Point){x*b,y*b};
    }
    bool operator < (const Point& b)const{
        return x < b.x || ( x==b.x && y < b.y) ;
    }
}pa[N],pb[N],ha[N],hb[N];
int na,nb,nha,nhb;
vector< pair<int,int> > edge;
int sgn(double x){
    if(fabs(x) < eps) return 0;
    if(x<0) return -1;
    return 1;
}
double cross(Point a,Point b){return a.x*b.y-b.x*a.y;}
double dot(Point a,Point b){return a.x*b.x + a.y*b.y;}
double len2(Point a){ return a.x*a.x + a.y*a.y;}
double len(Point a){return sqrt(len2(a));}
Point core(Point a,Point b,Point c){
    Point A=(Point){b.x-a.x,c.x-a.x}*2 , B = (Point){b.y-a.y,c.y-a.y}*2;
    Point C = (Point){ len2(b)-len2(a),len2(c)-len2(a) };
    return (Point){ cross(B,C)/cross(B,A),cross(A,C)/cross(A,B) };
}
void Andrew(Point p [],int n,Point ch[],int& m){
    sort(p,p+n);
    m = 0;
    for(int i = 0;i<n;++i){
        while( m > 1 && cross(p[i] - ch[m-2],ch[m-1] - ch[m-2])>=0) --m;
        ch[m++] = p[i];
    }
    int k = m;
    for(int i = n-2;i>=0;--i){
        while(m>k && cross(p[i] - ch[m-2] ,ch[m-1] - ch[m-2])>=0) --m;
        ch[m++] = p[i];
    }
    if(n>1) --m;
}
bool check(Point A[],int na,Point B[],int nb,int l,int r){
    if(na==1){
        return 1;
    }
    Point o = (A[l]+A[r])*0.5;
    double mi = -inf, mx = inf;
    int mid = -1;
    bool res = 1;
    for(int i = l+1;i<r;++i){
        Point c = core(A[l],A[r],A[i]);
        double d = len(c - o);
        if( sgn(cross(c-A[l],A[r]-A[l])) < 0 ) d = -d;
        if( mi < d  ){
            mi = d;
            mid = i;
        }
        if( mx <= mi ) res = 0;
    }
    for(int i = (r+1)%na ;i!=l;i = (i+1)%na ){
        Point c = core(A[l],A[r],A[i]);
        double d = len(c - o);
        if( sgn(cross(c-A[l],A[r]-A[l])) < 0 ) d = -d;
        if( mx > d  ) mx = d;
        if( mx <= mi) res = 0;
    }
    if( mx < mi + eps) res = 0;
    for(int i = 0;i<nb && res;++i){
        int fx = sgn(cross(B[i]-A[l],A[r]-A[l]));
        if(fx == 0){
            if(sgn(dot(A[r]-B[i],A[l]-B[i])) < 0 ) res = 0;
        }
        else{
            Point c = core(A[l],A[r],B[i]);
            double d = len(c-o);
            if( sgn(cross(c-A[l],A[r]-A[l])) < 0 ) d = -d;
            if(fx > 0 ){
                if(mx > d  ) mx = d;
            }
            else{
                if( mi < d ) mi = d;
            }
        }
        if( mx <= mi) res = 0;
    }
    return res || (mid!=-1 &&(check(A,na,B,nb,l,mid) || check(A,na,B,nb,mid,r)));
}
int main(){
    scanf("%d %d",&na,&nb);
    for(int i = 0;i<na;++i) scanf("%lf %lf",&pa[i].x,&pa[i].y);
    for(int i = 0;i<nb;++i) scanf("%lf %lf",&pb[i].x,&pb[i].y);
    Andrew(pa,na,ha,nha);
    Andrew(pb,nb,hb,nhb);
    if( check(ha,nha,pb,nb,0,nha-1) || check(hb,nhb,pa,na,0,nhb-1) ) puts("YES");
    else puts("NO");
    return 0;
}

 

2020.5.23：第二十二题：集训队训练，就一个扫描线，不写题解。

 

2020.5.29 ： 第二十三题：codeforces1359F 

详见：https://i.cnblogs.com/posts/edit-done;postId=12989198

2020.6.1 第二十四题：集训队训练，就是计几+状压dp，不写了

 

2020.6.7 第二十五提：集训队训练：http://codeforces.com/group/uVAsoW2Jkj/contest/283255/problem/F

没想到咕咕咕了那么多天，因为期末了，然后很多事要做，实训实验什么的。

题意：二维平面给了你15个矩形，坐标1000以内，然后问你一条长度为L的线段最多能和多少矩形接触。

题解：首先很容易发现答案线段的一个端点一定是矩形一条边上的一个点（s点），并且某个矩形的一个端点（t点）一定在答案线段上。然后想着证明别的更好的结论，但是太菜了证明半天没证明出来，但是我们发现这个结论也足够我们ac了。因为坐标1000，所以我们可以暴力枚举矩形端点以及边上整点来统计。但是有个很重要的问题就是，有可能答案线段的s点不是整点，比如黄色线段，那么如果我们枚举s点上下的整点，会出现一种情况就是刚好统计漏了答案，也就是红蓝线段所示。

但是有一个极其重要的证明就是，即使是上述情况，我们也可以通过枚举整点来统计出答案，因为从红色线段到蓝色线段中间肯定经过绿色线段（统计漏的答案矩形的端点），也就是绿色线段，所以我们还是能通过上述方法统计答案，最后就是大暴力了。复杂度5e7，但是可以剪枝优化，所以远远达不到（甚至还没优化就擦线过了。。）

 

 

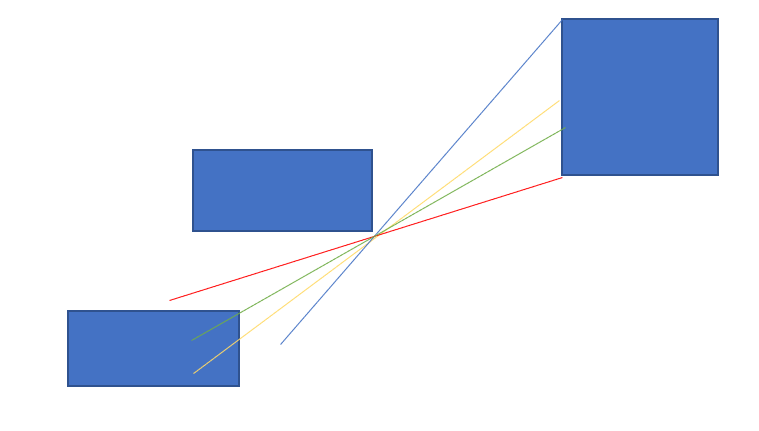
#include<bits/stdc++.h>
using namespace std;
typedef long double dd;
const dd eps = 1e-9;
int sgn(dd x){
    if(fabs(x) < eps ) return 0;
    if(x<0) return -1;
    return 1;
}
struct Point{
    dd x,y;
    Point operator + (const Point& b)const{
        return (Point){x+b.x,y+b.y};
    }
    Point operator - (const Point& b)const{
        return (Point){x-b.x,y-b.y};
    }
    Point operator / (const double& b)const{
        return (Point){x/b,y/b};
    }
    Point operator * (const double& b)const{
        return (Point){x*b,y*b};
    }
    dd len(){return sqrt(x*x+y*y); }
}p[5][16];
dd cross(Point a,Point b,Point c){
    return (b.x-a.x)*(c.y-a.y) - (c.x-a.x)*(b.y-a.y);
}
dd L;
int n;

//两线段是否相交
bool insert(Point s1,Point t1,Point s2,Point t2,bool show = 0 ){
    // if(show){
    //     // cerr<<s1.x<<" "<<s1.y<<" s1"<<endl;
    //     // cerr<<t1.x<<" "<<t1.y<<" t1"<<endl;
    //     // cerr<<s2.x<<" "<<s2.y<<" s2"<<endl;
    //     // cerr<<t2.x<<" "<<t2.y<<" t2"<<endl;
    //     // cerr<< cross(s1,s2,t1) <<" sgn1"<<endl;
    //     // cerr<< cross(s1,t2,t1) <<" sgn2"<<endl;
    //     // cerr<< cross(s2,s1,t2) <<" sgn3"<<endl;
    //     // cerr<< cross(s2,t1,t2) <<" sgn"<<endl;
    // }
    return
        max(s1.x,t1.x) >= min(s2.x,t2.x) &&
        max(s2.x,t2.x) >= min(s1.x,t1.x) &&
        max(s1.y,t1.y) >= min(s2.y,t2.y) &&
        max(s2.y,t2.y) >= min(s1.y,t1.y) &&
        sgn( cross(s1,s2,t1) ) * sgn( cross(s1,t2,t1) )<=0 &&
        sgn( cross(s2,s1,t2) ) * sgn( cross(s2,t1,t2) )<=0;
}
int solve(Point a,Point b){
    // Point test = a;
    Point s = b;
    Point deta = a - b;
    deta = deta*L/deta.len();
    a = b + deta;
    int res = 0;
    for(int i = 1;i<=n;++i){
        bool ok = 0;
        for(int k = 0;k<=3 && (!ok) ;++k){
            if( insert(b,a,p[k][i],p[k+1][i])) ok = 1;
        }
        if(ok) ++res;
    }
    return res;
}
int main(){
    int tL;
    scanf("%d %d",&n,&tL);
    L = tL;
    for(int i = 1;i<=n;++i){
        int xa,xb,ya,yb;
        scanf("%d %d %d %d",&xa,&ya,&xb,&yb);
        p[0][i].x = xa; p[0][i].y = ya;
        p[1][i].x = xb; p[1][i].y = ya;
        p[2][i].x = xb; p[2][i].y = yb;
        p[3][i].x = xa; p[3][i].y = yb;
        p[4][i] = p[0][i];
    }
    int ans = 1;
    for(int i = 1;i<=n;++i){
        for(int k = 0;k<4;++k){
            for(int j = 1;j<=n;++j){
                for(int x = p[0][j].x;x<=p[1][j].x;++x){
                    Point tem = (Point){1.0*x,p[0][j].y};
                    ans = max(ans,solve(p[k][i],tem));
                    tem.y = p[3][j].y;
                    ans = max(ans,solve(p[k][i],tem));
                }
                for(int y = p[0][j].y;y<=p[3][j].y;++y){
                    Point tem = (Point){p[0][j].x,1.0*y};
                    ans = max(ans,solve(p[k][i],tem));
                    tem.x = p[1][j].x;
                    ans = max(ans,solve(p[k][i],tem));
                }
            }
        }
    }
    printf("%d",ans);
}

 

由于搞项目，然后最近我们要选方向，我选了移动开发，所以又抽了点时间学安卓，然后又为了恢复就vp了几天，计几现在才做回来。

之前做了一道统计包含原点三角形的题，其实转换成不包含原点三角形就好了，就不贴了（25题）

 

2020.7.3第二十六题：codeforces886F

题意：给你2000个点，问你有多少条过原点的直线满足，所有点在该直线的投影点，是中心对称的。

看了看题解，知道做法就是：首先结论，如果投影中心对称，那么在该直线上这个中心对称点肯定是投影点的重心，那么反投影回去，也就是我对原来的点求个重心，那么最后投影中心肯定是重心的投影（写写柿子，用一个向量表示直线，然后投影用点积表示就知道了）

然后我们先把关于重心对称的点对删去，在剩下的点中枚举第一个点和谁对称，然后确定这条直线，然后扫一遍点判断直线符不符合即可。

这题由于担心被卡精度，所以全程用longlong，果然一切顺利哈哈哈

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e3+9;
bool used[N];
struct Point{
    ll x,y;
    Point operator + (const Point& b)const{
        return (Point){x+b.x,y+b.y};
    }
    Point operator / (const ll& b)const{
        return (Point){x/b,y/b};
    }
    Point operator * (const ll& b)const{
        return (Point){x*b,y*b};
    }
    Point rotate(){
        return (Point){-y,x};
    }
    bool operator < (const Point& b)const{
        if(x==b.x) return y < b.y;
        return x < b.x;
    }
    bool operator == (const Point& b)const{
        return x==b.x && y == b.y;
    }
    ll dot(const Point& b)const{
        return x*b.x + y*b.y;
    }
}pt[N],p0;
int n; 
vector<Point> p;
map<ll,int> mp;
map<double,int> line_vis;
void pre_solve(){
    for(int i = 1;i<=n;++i){
        if(used[i]) continue;
        for(int j = i+1;j<=n;++j){
            if(used[j]) continue;
            Point tp = (pt[i] + pt[j]);
            if( tp == p0 * 2){
                used[i] = used[j] = 1;
            }
        }
    }
    for(int i = 1;i<=n;++i){
        if(used[i]) continue;
        p.push_back(pt[i]);
    }
}
bool judge(Point line){
    mp.clear();
    ll p0_d = p0.dot(line);
    for(auto v : p){
        ll d = v.dot(line);
        d -= p0_d;
        mp[ d ]++;
    }
    for(auto it : mp){
        ll val = it.first;
        int num = it.second;
        if(val == 0  ) continue;
        if(mp[-val] != num) return 0;
    }
    return 1;
}
int main(){
    scanf("%d",&n);
    for(int i = 1;i<=n;++i){
        scanf("%lld %lld",&pt[i].x,&pt[i].y);
        pt[i] = pt[i] * n;
        p0 = p0 + pt[i];
    }
    if(n<=2){
        puts("-1");
        return 0;
    }
    p0 = p0 / n;
    pre_solve();
    if( p.size() == 0 ){
        puts("-1");
        return 0;
    }
    int ans= 0;
    for(int i = 0;i<p.size();++i){
        double tx = (p[0].x + p[i].x)*0.5;
        double ty = (p[0].y + p[i].y)*0.5;
        tx = p0.x - tx; ty = p0.y - ty;
        ll temx = 2*tx , temy = 2*ty;
        if(temy < 0 || (temy==0 && temx < 0)){
            temx = -temx;
            temy = -temy;
        }
        Point vec = (Point){temx,temy};

        double the = atan2(temy,temx);
        if(line_vis[the]) continue;
        line_vis[the] = 1;
        vec = vec.rotate();
        if(judge(vec)){
            ++ans;
            // cerr<<vec.x<<" "<<vec.y<<" vec"<<endl;
        }
    }
    printf("%d",ans);
    return 0;
}

 

2020.7.14 第二十七题：https://ac.nowcoder.com/acm/contest/5667/B

牛客多校第二场b题。。问所有过原点的圆中，给定点在其边上最多是多少。第一反应圆的反演，反演成直线，然后判断一条不过原点直线最多多少点在其上，结果。。反演后精度跪了，也就是判断反演后的点是不是在同一直线上精度误差不行，所以我们不应该判断是不是在同一直线上，而是通过反演图形，判断正形是不是在同一圆上来判断反演图形是不是统一直线上。（好像可以不用圆的反演做，可以根据圆的一些性质，比如中垂线，同一圆弧对角相同。。但是我第一反应就是定点圆。。圆的反演。。思路上秒杀。。）

#include<bits/stdc++.h>
using namespace std;
#define eps 1e-6
#define ld  double
const int N = 2e3+9;
int n,ans;
vector<int> maybe;
struct Point{
    ld x,y;
    int id;
    Point operator - (const Point& b)const{
        return (Point){x-b.x,y-b.y};
    }
    Point operator + (const Point& b)const{
        return (Point){x+b.x,y+b.y};
    }
    Point operator * (ld b){
        return (Point){b*x,y*b};
    }
    ld len(){
        return sqrt(x*x + y*y);
    }
    ld len2(){
        return x*x + y*y;
    }
}pt[N],p[N];
struct Circle{
    Point o;
    ld r;
};
ld cross(Point a, Point b){
    return a.x*b.y - b.x*a.y;
}
ld dot(Point a,Point b){
    return a.x*b.x + a.y*b.y;
}
ld dis(Point a,Point b){
    return sqrt( (a.x-b.x)*(a.x-b.x) + (a.y-b.y)*(a.y-b.y));
}
ld dis2(Point a,Point b){
    return (a.x-b.x)*(a.x-b.x) + (a.y-b.y)*(a.y-b.y);
}
   
int Quadrant(Point a)
{
    if(a.x>=0&&a.y>=0)  return 1;
    if(a.x<=0&&a.y>=0)  return 2;
    if(a.x<=0&&a.y<=0)  return 3;
    return 4;
}
bool cmp(Point a,Point b)  //先按象限从小到大排序 再按极角从小到大排序
{
    if(Quadrant(a)==Quadrant(b)){
        if( fabs( cross(a,b) ) < eps ) return a.len() < b.len();
        return cross(a,b) > 0;
    }
    else return Quadrant(a)<Quadrant(b);
}
Point Point_Inver(Circle c0,Point P){
    Point OP = P - c0.o;
    ld len = dis2(c0.o,P);
    return c0.o + OP*( c0.r * c0.r / len );
}
  
Point core(Point a,Point b,Point c){
    Point A=(Point){b.x-a.x,c.x-a.x}*2 , B = (Point){b.y-a.y,c.y-a.y}*2;
    Point C = (Point){ b.len2()-a.len2(),c.len2()-a.len2() };
    return (Point){ cross(B,C)/cross(B,A),cross(A,C)/cross(A,B) };
}
bool incir(Point o,double r,Point a){
    double d = dis(o,a);
    if(fabs(d-r) < eps ) return 1;
    return 0;
}
  
void solve(){
    if(n==1){
        ans = 1;
        return;
    }
    ans = 1;
    Point p0 = (Point){0,0};
    for(int i = 1;i<=n;++i){
        vector<Point> tem;
        for(int j = 1;j<=n;++j){
            if(j==i) continue;
            Point t = p[j] - p[i];
            t.id = p[j].id;
            tem.push_back(t);
        }
        sort(tem.begin(),tem.end(),cmp);
        for(int k = 0; k < tem.size();){
            // printf("%.12f\n", fabs(cross(p0,tem[k])) );
            if(  cross(pt[p[i].id] , pt[tem[k].id]) == 0 ){
                ++k;
                continue;
            }
            Point o = core(p0,pt[ p[i].id ] ,  pt[ tem[k].id ]);
            double r = o.len();
            int j = k;
            while( j + 1 < tem.size() &&  incir(o,r,pt[ tem[j+1].id ]) ){
                ++j;
            }
            ans = max(ans,j - k + 2);
            k = j + 1;
        }
    }
    // printf("%d",ans);
}
int main(){
    scanf("%d",&n);
    Circle c0;
    c0.o = (Point){0,0};
    c0.r = 200;
    for(int i =1;i<=n;++i){
        int x,y; scanf("%d %d",&x,&y);
        // scanf("%Lf %Lf",&pt[i].x,&pt[i].y);
        pt[i].x = x , pt[i].y = y;
        p[i] = Point_Inver(c0,pt[i]);
        p[i].id = i;
        // cerr<<i<<" "<<p[i].x<<" "<<p[i].y<<endl;
        // printf("%d %.12lf %.12lf\n",i,p[i].x,p[i].y);
    }
    solve();
    printf("%d",ans);
    // for(int i = 1;i<=n;++i) cerr<<p[i].x<<" "<<p[i].y<<" !"<<endl;
}

 

2020.7.14 第二十八题：http://bestcoder.hdu.edu.cn/contests/contest_showproblem.php?cid=893&pid=1001

给你两类点A，B类点，都是500个，问你用最少能用多少的A点包住B点。

一直以为是什么维护凸包。结果发现，枚举A中两点，假如B的点都在A左侧，那么则连一条有向边，最后就是变成图论，floyd求最小环

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define inf 0x3f3f3f3f
const int N = 500+9;
struct Point{
    int x,y;
}pn[N],pm[N];
int cross(Point a,Point b,Point c){
    return (b.x-a.x) * (c.y-a.y) - (c.x-a.x)*(b.y-a.y);
}
int dot(Point a,Point b,Point c){
    return (b.x-a.x)*(c.x-a.x) + (b.y-a.y)*(c.y-a.y);
}
int dis[N][N];
int n,m; 
bool onSeg(Point a,Point b,Point c){
    return dot(c,a,b) <= 0;
}
bool judge(int x,int y){
    for(int i = 1;i<=n;++i){
        if( cross(pm[x],pm[y],pn[i]) > 0 || cross(pm[x],pm[y],pn[i]) == 0 && onSeg(pm[x],pm[y],pn[i]) ) continue;
        return 0;
    }
    return 1;
}
void solve(){
    for(int k = 1;k<=m;++k){
        for(int i = 1;i<=m;++i){
            for(int j = 1;j<=m;++j){
                dis[i][j] = min(dis[i][j] , dis[i][k] + dis[k][j]);
            }
        }
    }
    int mi = inf;
    for(int i = 1;i<=m;++i) mi = min(mi,dis[i][i]);
    if( mi == inf ){
        puts("ToT");
    }
    else printf("%d\n",m-mi);
}
int main(){
    while(~scanf("%d",&n)){
        for(int i = 1;i<=n;++i) scanf("%d %d",&pn[i].x,&pn[i].y);
        scanf("%d",&m);
        for(int i = 1;i<=m;++i) scanf("%d %d",&pm[i].x,&pm[i].y);
        for(int i = 1;i<=m;++i) for(int j = 1;j<=m;++j) dis[i][j] = inf;
        for(int i = 1;i<=m;++i){
            for(int j = 1;j<=m;++j){
                if( j == i ) continue;
                if(judge(i,j)) dis[i][j] = 1;
            }
        }
        solve();
    }
}