莫比乌斯反演的学习
最近来学了一波经常遇到但一直没学的莫比乌斯函数。
其实莫比乌斯函数就是这个东西:
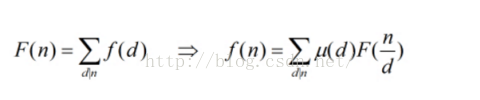
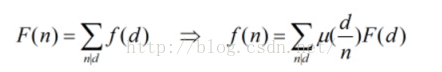
F(n) 推出 f(n) 就是反演。
求莫比乌斯:

1 void init(){ 2 mu[1] = 1; 3 for(int i = 2;i<=100000;++i){ 4 if(!vis[i]){ 5 prim.push_back(i); 6 mu[i] = -1; 7 } 8 for(int j = 0;j<prim.size() && i * prim[j] <= 100000;++j){ 9 vis[ i * prim[j] ] = 1; 10 if(i%prim[j]) mu[ i * prim[j] ] = -mu[i]; 11 else{ 12 mu[ i * prim[j] ] = 0; 13 break; 14 } 15 } 16 } 17 }
刷题:
求 [1...n] 区间 和 [1..m]区间中,gcd == 1 的二元组个数。把f(n)记为gcd == n 的二元组个数, F(n)记为 n | gcd 的二元组个数, 很容易知道 F(i) = n/i * m/i。反演求得f(1)

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const int N = 1e5+9; 5 bool vis[N]; 6 vector<int> prim; 7 int mu[N]; 8 void init(){ 9 mu[1] = 1; 10 for(int i = 2;i<=100000;++i){ 11 if(!vis[i]){ 12 prim.push_back(i); 13 mu[i] = -1; 14 } 15 for(int j = 0;j<prim.size() && i * prim[j] <= 100000;++j){ 16 vis[ i * prim[j] ] = 1; 17 if(i%prim[j]) mu[ i * prim[j] ] = -mu[i]; 18 else{ 19 mu[ i * prim[j] ] = 0; 20 break; 21 } 22 } 23 } 24 } 25 int main(){ 26 init(); 27 int T; scanf("%d",&T); 28 for(int cas = 1;cas<=T;++cas){ 29 int a,b,c,d,k; scanf("%d %d %d %d %d",&a,&b,&c,&d,&k); 30 if(k==0){ 31 printf("Case %d: 0\n",cas); 32 continue; 33 } 34 b/=k; d/=k; 35 ll ans1 = 0,ans2 = 0; 36 if(b>d) swap(b,d); 37 for(int i = 1;i<=min(b,d);++i){ 38 ans1 += 1ll * mu[i] * (b/i) * (d / i); 39 } 40 for(int i = 1;i<=b;++i){ 41 ans2 += 1ll * mu[i] * (b/i) * (b / i); 42 } 43 printf("Case %d: %lld\n",cas,ans1 - ans2/2); 44 } 45 return 0; 46 }
求 区间[a..b] 和区间[c..d]中 gcd == k 的二元组个数,就是上面那一题,加个容斥,然后注意到 (n/i) * (m/i) 这个东西会有连续的i是相同的, 所以 i 直接 跳到 n/(n/i) 这个位置,不然会tle

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const int N = 5e4+9; 5 bool vis[N]; 6 vector<int> prim; 7 int mu[N]; 8 int sum[N]; 9 void init(){ 10 mu[1] = 1; 11 for(int i = 2;i<=N-8;++i){ 12 if(!vis[i]){ 13 prim.push_back(i); 14 mu[i] = -1; 15 } 16 for(int j = 0;j<prim.size() && i * prim[j] <= N-8;++j){ 17 vis[ i * prim[j] ] = 1; 18 if(i%prim[j]) mu[ i * prim[j] ] = -mu[i]; 19 else{ 20 mu[ i * prim[j] ] = 0; 21 break; 22 } 23 } 24 } 25 for(int i= 1;i<=N-8;++i) sum[i] = sum[i-1] + mu[i]; 26 } 27 ll solve(int n,int m){ 28 ll ans = 0; 29 if(n>m) swap(n,m); 30 for(int i = 1;i<=min(n,m);){ 31 int j = min( n/(n/i) , m/(m/i) ); 32 ans += 1ll * (sum[j] - sum[i-1]) * (n/i) * (m / i); 33 i = j + 1; 34 } 35 return ans; 36 } 37 int main(){ 38 init(); 39 int T; scanf("%d",&T); 40 for(int cas = 1;cas<=T;++cas){ 41 int a,b,c,d,k; scanf("%d %d %d %d %d",&a,&b,&c,&d,&k); 42 if(k==0){ 43 printf("Case %d: 0\n",cas); 44 continue; 45 } 46 --a; --c; 47 b/=k; d/=k; 48 a/=k; c/=k; 49 printf("%lld\n",solve(b,d) - solve(a,d) - solve(c,b) + solve(a,c)); 50 } 51 return 0; 52 }
求区间[1..n] 和 区间 [1..m]中gcd 的 质因子(带重复)的个数小于 P 的对数。
代码:

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const int N = 5e5+9; 5 bool vis[N]; 6 int mu[N],sum[27][N],cnt[N]; 7 vector<int> prim; 8 void Mobi(){ 9 mu[1] = 1; cnt[1] = 0; 10 for(int i = 2;i<=N-9;++i){ 11 if(!vis[i]){ 12 prim.push_back(i); 13 mu[i] = -1; 14 cnt[i] = 1; 15 } 16 for(int j = 0;j<prim.size() && i * prim[j] <= N-9;++j){ 17 vis[ i * prim[j] ] = 1; 18 cnt[ i * prim[j] ] = cnt[i] + 1; 19 if( i % prim[j] ) mu[ i * prim[j] ] = -mu[i]; 20 else{ 21 mu[i * prim[j] ] = 0; 22 break; 23 } 24 } 25 } 26 } 27 void init(){ 28 for(int i = 1;i<=N-9;++i){ 29 for(int j = i;j<= N - 9;j+=i){ 30 sum[ cnt[i] ][ j ] += mu[j/i]; 31 } 32 } 33 for(int i = 1;i<=N-9;++i){ 34 for(int j = 1;j<=20;++j){ 35 sum[j][i] += sum[j-1][i]; 36 } 37 } 38 for(int i = 0;i<=20;++i){ 39 for(int j = 1;j<=N-9;++j){ 40 sum[i][j] += sum[i][j-1]; 41 } 42 } 43 } 44 int main(){ 45 Mobi(); 46 init(); 47 int T; scanf("%d",&T); 48 while(T--){ 49 int n,m,p; scanf("%d %d %d",&n,&m,&p); 50 if(p>20){ 51 printf("%lld\n",1ll * n * m); 52 continue; 53 } 54 if(n>m) swap(n,m); 55 ll ans = 0; 56 for(int i = 1;i<=n;){ 57 int j = min( n/(n/i) , m/(m/i) ); 58 ans += 1ll * (n/i) * (m/i) * (sum[p][j] - sum[p][i-1]); 59 i = j+1; 60 // cerr<<i<<" "<<j<<" "<<ans<<endl; 61 } 62 printf("%lld\n",ans); 63 } 64 }
给你一个长度n的数组a,a[i] <= m ,给你一个数k,对于 1 到 m 的 每个数 d ,询问有多少 序列 b 满足 b[i] != a[i] 的 i 仅有 k 个, 并且 gcd (b[1]...b[n]) == d
还是那个反演,只不过加了一个组合数。

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const int N = 3e5+9; 5 const ll modd = 1e9+7; 6 vector<int> prim; 7 bool vis[N]; 8 ll mu[N],a[N],F[N],X[N]; 9 ll jie[N]; 10 int num[N]; 11 int n,m,k; 12 ll ksm(ll a,ll b){ 13 ll res = 1; 14 a %= modd; 15 while(b){ 16 if(b&1) res = res * a % modd; 17 b>>=1; 18 a = a * a % modd; 19 } 20 return res; 21 } 22 ll C(ll n,ll m){ 23 ll tem = jie[m] * jie[n-m] % modd; 24 return jie[n] * ksm(tem,modd-2) % modd; 25 } 26 void Mobi(){ 27 mu[1] = 1; 28 for(int i = 2;i<=N-9;++i){ 29 if(!vis[i]){ 30 prim.push_back(i); 31 mu[i] = -1; 32 } 33 for(int j = 0;j<prim.size() && i * prim[j] <= N - 9;++j){ 34 vis[ i * prim[j] ] = 1; 35 if( i% prim[j] ) mu[i * prim[j] ] = -mu[i]; 36 else{ 37 mu[i*prim[j]] = 0; 38 break; 39 } 40 } 41 } 42 jie[0] = 1; 43 for(int i = 1;i<=N-9;++i) jie[i] = jie[i-1] * i % modd; 44 } 45 void init(){ 46 for(int i = 1;i<=m;++i) X[i] = n; 47 for(int i = 1;i<=m;++i){ 48 for(int j = i;j<=m;j+=i){ 49 X[i] -= num[j]; 50 } 51 } 52 for(int i = 1;i<=m;++i){ 53 if(X[i] > k) F[i] = 0; 54 else{ 55 F[i] = ksm( m/i , X[i] ) * C(n-X[i],k-X[i]) % modd * ksm( m/i - 1 , k-X[i]) % modd; 56 } 57 } 58 } 59 int main(){ 60 Mobi(); 61 while(~scanf("%d %d %d",&n,&m,&k)){ 62 for(int i = 1;i<=m;++i) num[i] = 0; 63 for(int i = 1;i<=n;++i){ 64 scanf("%lld",a+i); 65 num[ a[i] ]++; 66 } 67 init(); 68 for(int i = 1;i<=m;++i){ 69 ll ans = 0; 70 for(int j = i;j<=m;j+=i){ 71 ans = (ans + mu[j/i] * F[j] + modd)%modd; 72 } 73 printf("%lld%c",ans,i==m?'\n':' '); 74 } 75 } 76 return 0; 77 }
给你一个长度n的数组a,问你有多少个 子序列满足 gcd == 1.同一个套路, 对于每个d,求出 有多少个 数 是 d 的倍数(num),直接 mu[d] * F(d) == mu[d] * ( ksm(2,num) -1 )

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const ll modd = 1e9+7; 5 const int N = 1e5+9; 6 bool vis[N]; 7 vector<int> prim; 8 ll mu[N],num[N]; 9 map<int,int> mp; 10 ll ksm(ll a,ll b){ 11 ll res = 1; 12 while(b){ 13 if(b&1) res = res * a % modd; 14 b>>=1; 15 a = a * a % modd; 16 } 17 return res; 18 } 19 void Mobi(){ 20 mu[1] = 1; 21 for(int i = 2;i<=100000;++i){ 22 if(!vis[i]){ 23 prim.push_back(i); 24 mu[i] = -1; 25 } 26 for(int j = 0;j<prim.size() && i * prim[j] <= 100000;++j){ 27 vis[ i * prim[j] ] = 1; 28 if(i%prim[j]) mu[ i * prim[j] ] = -mu[i]; 29 else{ 30 mu[ i * prim[j] ] = 0; 31 break; 32 } 33 } 34 } 35 } 36 int main(){ 37 Mobi(); 38 int n; scanf("%d",&n); 39 int m = 0; 40 for(int i = 1;i<=n;++i){ 41 int a; scanf("%d",&a); 42 mp[a]++; 43 m = max(m,a); 44 } 45 for(int i = 1;i<=m;++i){ 46 for(int j = i;j<=m;j+=i){ 47 num[i] += mp[j]; 48 } 49 } 50 ll ans = 0; 51 for(int i = 1;i<=m;++i){ 52 ll tem = mu[i] * (ksm(2,num[i])-1); 53 ans = (ans + tem + modd) % modd; 54 } 55 printf("%lld",ans); 56 return 0; 57 }
同样的套路

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const int N = 1e5+9; 5 bool vis[N]; 6 vector<int> prim; 7 ll f[N],mu[N]; 8 void init(){ 9 mu[1] = 1; 10 for(int i =2;i<=N-9;++i){ 11 if(!vis[i]){ 12 prim.push_back(i); 13 mu[i] = -1; 14 } 15 for(int j = 0;j<prim.size() && i * prim[j] <= N-9;++j){ 16 vis[ i * prim[j] ] = 1; 17 if( i % prim[j] ) mu[i * prim[j] ] = -mu[i]; 18 else{ 19 mu[ i * prim[j] ] = 0; 20 break; 21 } 22 } 23 } 24 } 25 int main(){ 26 init(); 27 int n,m; scanf("%d %d",&n,&m); 28 for(int i = 1;i<=min(n,m);++i){ 29 for(int j = i;j<=min(n,m);j+=i){ 30 f[i] += mu[j/i] * (n/j) * (m/j); 31 } 32 } 33 ll ans = 0; 34 for(int i = 1;i<=min(n,m);++i){ 35 ans += f[i] * (2*i-1); 36 } 37 printf("%lld",ans); 38 return 0; 39 }
嗯,刷了几道莫比乌斯的题目,算是可以自保了,毕竟不是数学选手,就学到这里算了。哈哈哈。





