圆的反演（hdu4773，hdu6158，hdu6097）

hdu4773：http://acm.hdu.edu.cn/showproblem.php?pid=4773

题意：给你两个相离的圆，以及一个点，求所有和这两个圆相切，并且经过该点的圆。

我们先画出满足题意的圆，然后把这三个圆反演，给定的两个圆因为不经过p点，反演后是两个圆，然后ans圆经过p点，所以反演后是一条直线，又因为和两个圆相切，所以反演出来的直线也是和两个圆相切的，所以就是两个反演圆的外公切线了（不可以是内公切先，画画图就明白了）。

#include<bits/stdc++.h>
using namespace std;
#define eps 1e-6
int sgn(double x){
    if( fabs(x) < eps) return 0;
    if( x < 0) return -1;
    return 1;
}
struct Point{
    double x,y;
    Point operator - (const Point& b){
        return (Point){ x - b.x,y-b.y};
    }
    Point operator + (const Point& b){
        return (Point){x+b.x,y+b.y};
    }
    Point operator * (const double& b){
        return (Point){b * x,b * y};
    }
    Point Move(double a,double d){
        return (Point){ x + d * cos(a),y + d * sin(a)};
    }
};
struct Circle{
    Point o;
    double r;
}c[3],c0,ansc[3];
int tot;
double cross(Point a,Point b,Point c){
    return (b.x - a.x) * (c.y - a.y) - (c.x - a.x)*(b.y - a.y);
}
double dot(Point a,Point b,Point c){
    return (b.x - a.x) * (c.x - a.x) + (b.y - a.y) * (c.y - a.y);
}
double dis(Point a,Point b){
    return sqrt( (a.x - b.x) * (a.x - b.x) + (a.y - b.y)*(a.y - b.y));
}
Point Point_Inver(Circle c0,Point P){
    Point OP = P - c0.o;
    double len = dis(c0.o,P);
    len = len*len;
    return c0.o + OP*( c0.r * c0.r / len );
}
Circle Circle_Inver(Circle c0,Circle a){
    Circle res;
    Point OA = a.o - c0.o;
    double len = dis(a.o,c0.o);
    Point up = c0.o + OA * ( ( len + a.r) / len );
    Point down = c0.o + OA *( (len - a.r) / len );
    up = Point_Inver(c0,up);
    down = Point_Inver(c0,down);
    res.o = (up+down) * 0.5;
    res.r = dis(up,down) * 0.5;
    return res;
}
Circle Line_Inver(Circle c0,Point a,Point b){
    Circle res;
    double d = fabs( cross(a,c0.o,b) / dis(a,b));
    res.r = c0.r * c0.r / (2.0 * d);

    double len = dot(a,b,c0.o) / dis(a,b);
    Point AB = b - a;
    Point c = a + AB * (len/dis(a,b));
    Point CO = c - c0.o;
    res.o = c0.o + CO * (res.r/d);

    //double len = dis(a,c[1].o);
    //res.o = c0.o + (a-c[1].o) * (res.r/len);
    return res;
}
void solve(){
    for(int i = 1;i<=2;++i) c[i] = Circle_Inver(c0,c[i]);
    if( c[1].r < c[2].r - eps) swap(c[1],c[2]);
    Point v = c[2].o - c[1].o;
    double a1 = atan2(v.y,v.x);
    double a2 = acos( (c[1].r - c[2].r) / dis(c[1].o,c[2].o));
    Point p1 = c[1].o.Move(a1 + a2,c[1].r);
    Point p2 = c[2].o.Move(a1 + a2,c[2].r);
    //cerr<<p1.x<<" "<<p1.y<<" "<<p2.x<<" "<<p2.y<<endl;
    if( sgn(cross(c[1].o,p1,p2)) == sgn(cross(c0.o,p1,p2)) ) ansc[++tot] = Line_Inver(c0,p1,p2);
    p1 = c[1].o.Move(a1-a2,c[1].r);
    p2 = c[2].o.Move(a1-a2,c[2].r);
    //cerr<<p1.x<<" "<<p1.y<<" "<<p2.x<<" "<<p2.y<<endl;
    if( sgn(cross(c[1].o,p1,p2)) == sgn(cross(c0.o,p1,p2)) ) ansc[++tot] = Line_Inver(c0,p1,p2);
}
int main(){
    c0.r = 10.0;
    int T; scanf("%d",&T);
    while(T--){
        tot = 0;
        for(int i = 1;i<=2;++i) scanf("%lf %lf %lf",&c[i].o.x,&c[i].o.y,&c[i].r);
        scanf("%lf %lf",&c0.o.x,&c0.o.y);
        solve();
        printf("%d\n",tot);
        for(int i = 1;i<=tot;++i) printf("%.8f %.8f %.8f\n",ansc[i].o.x,ansc[i].o.y,ansc[i].r);
    }
    return 0;
}

 

 

hdu6158:http://acm.hdu.edu.cn/showproblem.php?pid=6158 

 

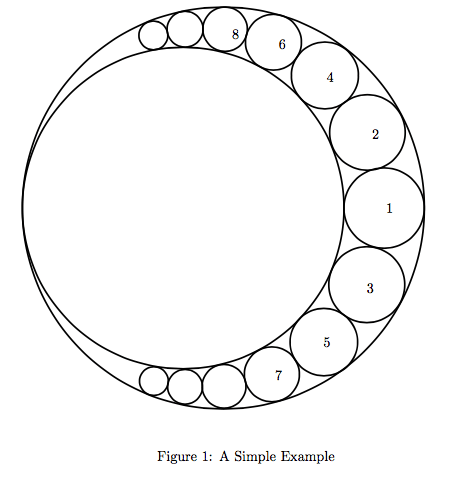
 给你这两个大圆的半径，问你往里面塞n个小圆，这n个小圆面积和是多少。

题解：很明显是以左边的切点做圆心，半径1的圆，对这两个大圆做圆的反演，然后就反演出两条平行直线了（画画图发现两条直线平行y轴），其他小圆因为和两大圆相切，所以和两直线相切，也就是夹在中间的那一堆圆，直接算就OK了。

参考博客：https://www.cnblogs.com/flipped/p/7397942.html

#include<bits/stdc++.h>
using namespace std;
#define eps 1e-8
const double rr = 1.0;
const double pi = acos(-1.0);
double r1,r2;
int n;
double area(double x){return pi*x*x;}
double yan(int id){
    double x = rr*(r2 + r1)/r1/r2/4;
    double r = rr/r1/2 - x;
    double y = 2 * id * r;
    double len = sqrt(x*x+y*y);
    double d1 = len - r,d2 = len + r;
    double R = rr * ( 1/d1 - 1/d2) * 0.5;
    return area(R);
}
double solve(){
    double ans = 0;
    ans += area( (r2-r1) );
    --n;
    for(int i = 1;i<=(n+1)/2;++i){
        double tem = yan(i);
        ans += tem;
        if( i * 2 <= n ) ans += tem;
        if( tem * (n-i*2) < eps ) break;
    }
    return ans;
}
int main(){
    int T; scanf("%d",&T);
    while(T--){
        scanf("%lf %lf",&r1,&r2);
        if(r1 > r2) swap(r1,r2);
        scanf("%d",&n);
        printf("%.5f\n",solve());
    }
    return 0;
}

 

hdu6097：http://acm.hdu.edu.cn/showproblem.php?pid=6097

#include<bits/stdc++.h>
using namespace std;
#define eps 1e-6
struct Point{
    double x,y;
}p1,q1,p2,q2,o;
double dis2(Point a,Point b){
    return (a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y);
}
double dis(Point a,Point b){
    return sqrt( dis2(a,b) );
}
double r;
Point change(Point a){
    Point res = a;
    double len2 = dis2(a,o);
    res.x = a.x * ( r * r /len2);
    res.y = a.y * ( r * r /len2);
    return res;
}
void solve(){
    double pd = dis(p1,o);
    if(pd < eps){
        printf("%.7f\n",2 * r);
        return;
    }
    p2 = change(p1);
    q2 = change(q1);
    Point f;
    f.x = ( p2.x + q2.x ) /2;
    f.y = ( p2.y + q2.y ) /2;
    double fd = dis(f,o);
    //cerr<<fd<<" "<<f.x<<" "<<f.y<<" "<<p2.x<<" "<<p2.y<<" "<<q2.x<<" "<<q2.y<<endl;
    double ans;
    if( r - fd > -eps){
        //cerr<<"ok1"<<endl;
        ans = dis(q2,p2);
        ans *= pd/r;
    }
    else{
        //cerr<<"ok2"<<endl;
        Point D;
        D.x = f.x * r / fd;
        D.y = f.y * r / fd;
        ans = 2 * dis(D,p1);
    }
    printf("%.7f\n",ans);
}
int main(){
    int T; scanf("%d",&T);
    o.x = o.y = 0;
    while(T--){
        scanf("%lf %lf %lf %lf %lf",&r,&p1.x,&p1.y,&q1.x,&q1.y);
        solve();
    }
    return 0;
}