机器学习之集成学习
1. 什么是集成学习?
如果你随机向几千个人询问一个复杂问题,然后汇总它们的答案。在许多情况下你会发现,这个汇总的回答比专家的答案还要好,这被称为集体智慧,同样,如果你聚合一组预测器的预测,得到的预测结果也比最好的单个预测器要好,这样的一组预测器,我们称为集成,也被称为集成学习。集成学习可以用于分类问题集成,回归问题集成,特征选取集成,异常点检测集成等等,可以说所有的机器学习领域都可以看到集成学习的身影。
集成学习有两个主要的问题需要解决:
- 如何得到若干个个体学习器
- 如何选择一种结合策略,将这些个体学习器集合成一个强学习器
2. 集成学习之结合策略
2.1 个体学习器已知的情况下
blending就是将所有已知的个体学习器g(t)结合起来,发挥集体的智慧得到G强学习器 。值得注意的一点是这里的g(t)都是已知的。blending通常有三种形式:
- uniform:简单地计算所有g(t)的平均值
- non-uniform:所有g(t)的线性组合
- conditional:所有g(t)的非线性组合
其中,uniform采用投票、求平均的形式更注重稳定性,而non-uniform和conditional追求的更复杂准确的模型,但存在过拟合的危险

2.2 个体学习器未知的情况下
blending是建立在所有g(t)已知的情况。那如果所有个体学习器g(t)未知的情况,对应的就是学习法,做法就是一边学g(t),一边将它们结合起来。学习法通常也有三种形式(与blending的三种形式一一对应):
- Bagging:通过bootstrap方法,得到不同g(t),计算所有g(t)的平均值
- AdaBoost:通过bootstrap方法,得到不同g(t),所有g(t)的线性组合
- Decision Tree:通过数据分割的形式得到不同的g(t),所有g(t)的非线性组合

除了这些基本的集成模型之外,我们还可以把某些模型结合起来得到新的集成模型,例如:
- Bagging与Decision Tree结合起来组成了Random Forest。Random Forest中的Decision Tree是比较“茂盛”的树,即每个树的g(t)都比较强一些。
- AdaBoost与Decision Tree结合组成了AdaBoost-DTree。AdaBoost-DTree的Decision Tree是比较“矮弱”的树,即每个树的g(t)都比较弱一些,由AdaBoost将所有弱弱的树结合起来,让综合能力更强。
- GradientBoost与Decision Tree结合就构成了经典的算法GBDT。

2.3 集成学习优点
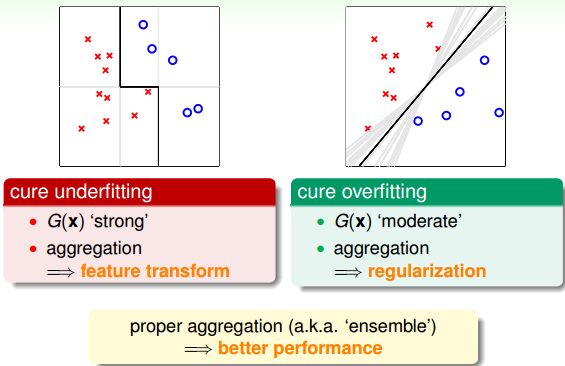
集成的核心是将所有的g(t)结合起来,融合到一起,即集体智慧的思想。这种做法之所以能得到很好的模型g(t),是因为集成具有两个方面的优点:cure underfitting和cure overfitting。
-
集成 models 有助于防止欠拟合(underfitting)。它把所有比较弱的 结合起来,利用集体智慧来获得比较好的模型 。集成就相当于是特征转换,来获得复杂的学习模型。
-
第二,集成 models 有助于防止过拟合(overfitting)。它把所有 进行组合,容易得到一个比较中庸的模型,类似于SVM的最大间隔一样的效果,从而避免一些极端情况包括过拟合的发生。从这个角度来说,集成起到了正则化的效果。
由于集成具有这两个方面的优点,所以在实际应用中集成 models 都有很好的表现
注:以上内容摘抄自:https://zhuanlan.zhihu.com/p/32412775,感谢博主分享
3. Bagging和Pasting
Bagging和Posting方法在训练过程中,各基分类器之间无强依赖,可以并行进行训练,其中很著名的算法之一是基于决策树基分类器的随机森林(random forest)。
为了让基分类器之间相互独立,将训练集分为若干子集(当训练样本较少时,子集之间可能有重叠)。该方法更像是一个集体决策的过程,每个个体都进行单独学习,学习的内容可以相同,可以不同,也可以部分重叠,但由于个体之间存在差异,最终做出的判断不会完全一致,在最终做决策时,每个个体单独做出判断,再通过投票的方式做出最后的集体决策
Bagging和Posting的唯一区别在于对于同一个基分类器抽样的样本数据是否可以放回,bagging抽样后的数据可以放回继续抽样,但posting抽样后的数据不可以放回,换句话说,bagging和pasting都允许训练实例在多个预测器中被多次采样名单是只有bagging允许训练实例被同一个预测器多次采样
由于bagging和Posting是并行训练机制,所以可以通过不同的cpu内核甚至是不同的服务器并行地训练预测器和分类,这也正是bagging和pasting方法如此流行的原因之一,它们非常易于扩展
4. Boosting
Boosting方法训练基分类器时采用串行的方式,各个基分类器之间有依赖
它的基本思想是将基分类器层层叠加,每一层在训练的时候,对前一层基分类器分错的样本,给与更高的权重,测试时,根据各层分类器的结果的加权得到最终的结果,这涉及到两组加权系数,将在Adaboost算法中详细说明
Boosting的过程很类似于人类学习的过程,我们学习新知识的过程往往是迭代的,第一遍学习的时候,我们会记住一部分知识,但往往也会犯一些错误,对于这些错误,我们的印象会很深,在第二遍学习的时候,就会针对犯过的错误的只是加强学习,以减少类似的错误发生,不断循环往复,直到犯错误的次数减少到很低的程度
4.1 AdaBoost
AdaBoost算法:
- (1) 初始化每个实例权重\(w^{(i)} = \frac{1}{m}\),m为样本个数
- (2) 使用第一个预测器训练,计算其误差率\(r_1\) $$r_j = \frac{\sum_{i=1,j_{j}{(i)}!=y{(i)}}mw{i}}{\sum_{i=1}mw{(i)}}$$
- (3) 计算预测器的权重,预测器的准确率越高,其权重就越高,如果只是随机猜测,则其权重接近于零。但是,如果大部分情况下它都是错的(也就是准确率比随机猜测还低),那么它的权重为负$$\alpha_j = \eta \log \frac{1-r_j}{r_j}$$,\(\eta为学习率超参数,默认为1\)
- (4) 对每个实例的权重进行更新$$w^{{i}} \leftarrow \begin{cases}
w{(i)}&(y_j == y^{(i)})\
w^{(i)}\exp(a_j)& (y_j^{(i)} != y^{(i)})
\end{cases}$$ - (5) 将所有实例的权重归一化(即除以\(\sum_{i=1}^mw^{(i)}\))
- (6) 使用更新后的权重训练一个新的预测器,然后重复整个过程(计算新预测器的权重,更新实例权重,然后对另一个预测器进行训练)
- (7) 当到达所需数量的预测器或得到完美的预测器时,算法停止
预测的时候,AdaBoost就是简单地计算所有预测器的预测结果,并使用预测其权重对它们进行加权,最后,得到大多数加权投票的类别就是预测器给出的预测类别
4.2 梯度提升
另一个非常受欢迎的提升法是梯度提升(Gradient Boosting),跟AdaBoost一样,梯度提升也是逐步在集成中添加预测器,每一个都对前序做出改正,不同之处在于,它不像Adaboost那样在每个迭代中调整实例权重,而是让新的预测器针对前一个预测器的残差进行拟合
举个简单的回归示例,使用决策树作为基础预测器(梯度提升当然也适用于回归任务),这被称为梯度树提升或者梯度提升回归树(DBRT)
from sklearn.tree import DecisionTreeRegressor
tree_reg1 = DecisionTreeRegressor(max_depth=2)
tree_reg1.fit(x,y)
现在针对第一个预测器的残差,训练第二个DecisionTreeRegressor
y2 = y - tree_reg1.predict(x)
tree_reg2 = DecisionTreeRegressor(max_depth=2)
tree_reg2.fit(x,y2)
然后,针对第二个预测器的残差,训练第三个回归器
y3 = y2 - tree_reg1.predict(x)
tree_reg2 = DecisionTreeRegressor(max_depth=2)
tree_reg2.fit(x,y3)
现在,有了一个包含三棵树的集成,将所有树的预测相加,从而对新实例进行预测相加,从而对新实例进行预测
y_pred = sum(tree.predict(x_new) for tree in (tree_reg1,tree_reg2,tree_reg3))
5. sklearn集成学习实践
5.1 训练随机森林分类器
在<机器学习之决策树原理和sklearn实践>博文中为卫星数据训练的决策树基础上训练一个随机森林分类器
需求:
- a.生产1000个训练集子集,每个子集包含随机挑选的100个实例,提示:使用sklearn的ShuffleSplit来实现
- b.使用之前得到的超参数,在每个子集上训练一个决策树,在测试集上评估这1000个决策树。因为训练集更小,所以这些决策树的表现可能比第一个决策树要差一点
- c.用每个测试集实例,生成1000个决策树的预测,然后仅保留次数最频繁的预测(可以使用Scipy的mode()函数),这样你在测试集上获得大多数投票的结果
- d.评估测试集上的这些预测,你得到的准确率应该比第一个模型更高
代码实现:
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split,ShuffleSplit
dataset = make_moons(n_samples=10000,noise=0.4)
features,labels = dataset[0],dataset[1]
x_train,x_test = train_test_split(features,test_size=0.2,random_state=42)
y_train,y_test = train_test_split(labels,test_size=0.2,random_state=42)
train_subset = []
# 创建1000个训练子集
ss = ShuffleSplit(n_splits=1000,test_size = 0.01,train_size=0.01,random_state=42)
for train_index,_ in ss.split(features):
train_subset.append((features[train_index],labels[train_index]))
# 使用x_train和y_train训练一个决策时
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import accuracy_score
decisionTree = DecisionTreeClassifier(criterion='gini')
param_grid = {'max_leaf_nodes': [i for i in range(2,10)]}
gridSearchCV = GridSearchCV(decisionTree,param_grid=param_grid,cv=3,verbose=1)
gridSearchCV.fit(x_train,y_train)
y_prab = gridSearchCV.predict(x_test)
print('accuracy score:',accuracy_score(y_test,y_prab))
print(gridSearchCV.best_params_)
print(gridSearchCV.best_estimator_)
Fitting 3 folds for each of 8 candidates, totalling 24 fits
accuracy score: 0.8525
{'max_leaf_nodes': 9}
DecisionTreeClassifier(class_weight=None, criterion='gini', max_depth=None,
max_features=None, max_leaf_nodes=9, min_impurity_decrease=0.0,
min_impurity_split=None, min_samples_leaf=1,
min_samples_split=2, min_weight_fraction_leaf=0.0,
presort=False, random_state=None, splitter='best')
[Parallel(n_jobs=1)]: Using backend SequentialBackend with 1 concurrent workers.
[Parallel(n_jobs=1)]: Done 24 out of 24 | elapsed: 0.0s finished
# 克隆1000个决策树
from sklearn.base import clone
import numpy as np
estimators = [clone(gridSearchCV.best_estimator_) for _ in range(1000)]
#在测试集上评估这1000个决策树
accuracy_score_array = []
for tree, (x_mini_train, y_mini_train) in zip(estimators, train_subset):
tree.fit(x_mini_train, y_mini_train)
y_predict = tree.predict(x_test)
accuracy_score_array.append(accuracy_score(y_test,y_predict))
print('avg accuracy_score:', np.mean(accuracy_score_array))
avg accuracy_score: 0.815643
# 用每个测试集实例,生成1000个决策树的预测,然后仅保留次数最频繁的预测
y_pred = np.zeros((len(estimators),len(x_test)),dtype=np.uint8)
for tree_index, tree in enumerate(estimators):
y_pred[tree_index] = tree.predict(x_test)
from scipy.stats import mode
y_pred_majority_votes, n_votes = mode(y_pred, axis=0)
print(accuracy_score(y_test, y_pred_majority_votes.reshape([-1])))
0.8605
5.1 RandomForestClassifier随机森林分类器
通过4.1已经发现,随机森林是决策树的集成,通常用bagging(有时也可能是pasting)方法训练,构成随机森林分类器有两种方法:
-
(1)先构建一个BaggingClassifier然后将结果传输到DecisionTreeClassifier
bag_clf = BaggingClassifier(
DecisionTreeClassifier(splitter='random',max_leaf_nodes=16),
n_estimators=500,max_samples=1.0,bootstrap=True,n_jobs=-1) -
(2) 使用RandomForestClassifier类,这种方法更方便,对决策树更优化(同样,对于回归任务也有一个RandomForestRegresson类)
from sklearn.ensemble import RandomForestClassifier
rnd_clf = RandomForestClassifier(n_estimators=500,max_leaf_nodes=16,n_jobs=-1)
rnd_clf.fit(x_train,y_train)
y_pred_rf = rnd_clf.predict(x_test)
RandomForestClassifier具有DecisionTreeClassifier的所有超参数,已经BaggingClassifier的所有超参数,前者用来控制树的生长,后者用来控制集成本身
随机树的生长引入了更多的随机性:分裂节点时不再是搜索最好的特征,而是在一个随机生成的子集里搜索最好的特征,这导致决策树具有更大的随机性,用更高的偏差换取更低的方差,总之,还是产生了一个整体性能更优的模型
重要特征:
单看一颗决策树,重要的特征更可能出现在靠近根节点的位置,而不重要的特征通常出现在靠近叶节点的位置(甚至根本不出现),因此,通过计算一个特征在森林中所有树上的平均深度,可以算出一个特征的重要程度
sklearn在训练结束后会自动计算每个特征的重要性,通过变量feature_importances_可以访问到这个结果
5.3 ExtraTreesClassifier极端随机树
随机森林里单棵树的生长过程中,每个节点在分裂时仅考虑到了一个随机子集所包含的特征,如果我们对每个特征使用随机阈值,而 不是搜索得出的最佳阈值(如常规决策树),则可能让决策树生长得更加随机,这种极端随机得决策树组成的森林,被称为极端随机树集成。
同样,它也是以更高的偏差换取最低的方差,极端随机树训练起来比常规随机森林要快得多,因为在每个节点上找到每个特征的最佳阈值是决策树生长中最耗时的任务之一
- 通常来说,很难预先知道一个RandomForestClassifier是否比一个ExtraTreesClassifier更好或是更差,唯一的方法是两种都尝试一遍,然后使用交叉验证(还需要使用网格搜索调整超参数)进行比较
参考资料:


