机器学习之支持向量机原理和sklearn实践
1. 场景描述
问题:如何对对下图的线性可分数据集和线性不可分数据集进行分类?
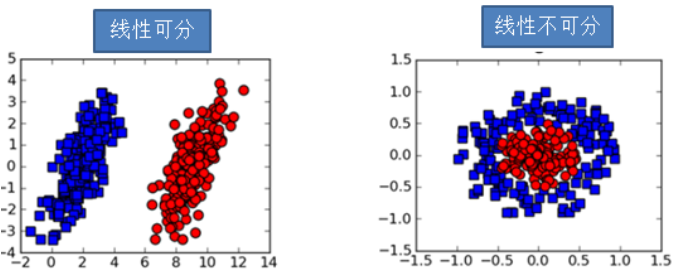
思路:
- (1)对线性可分数据集找到最优分割超平面
- (2)将线性不可分数据集通过某种方法转换为线性可分数据集
下面将带着这两个问题对支持向量机相关问题进行总结
2. 如何找到最优分割超平面
一般地,当训练数据集线性可分时,存在无穷个分离超平面可将两类数据正确分开,比如感知机求得的分离超平面就有无穷多个,为了求得唯一的最优分离超平面,就需要使用间隔最大化的支持向量机
2.1 分类预测确信度
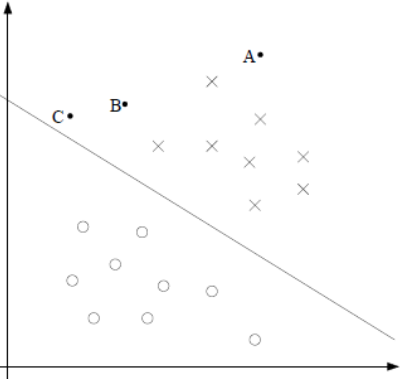
上图中,有A,B,C三个点,表示三个示例,均在分离超平面的正类一侧,点A距分离超平面较远,若预测点为正类,就比较确信预测是正确的;点C距离超平面较近,若预测该点为正类,就不那么确信;点B介于点A与C之间,预测其为正类的确信度也在A与C之间
通过上面的描述,当训练集中的所有数据点都距离分隔平面足够远时,确信度就越大。在超平面\(w^T X + b = 0\)确定的情况下,可以通过函数间隔和几何间隔来确定数据点离分割超平面的距离
2.2 函数间隔
对于给定的训练数据集T和超平面(w,b),定义超平面(w,b)关于样本\((x_i,y_i)\)的函数间隔为:$$\overline{\gamma{_i}} = y_i(w\bullet{x_i} + b)$$
定义超平面(w,b)关于训练数据集T的函数间隔为超平面(w,b)关于T中所有样本点\((x_i,y_i)\)的函数间隔之最小值:$$\overline{\gamma} = \min\limits_{i=1,...,N}\overline{\gamma{_i}}$$
函数间隔可以表示分类预测的正确性及确信度,但是选择分离超平面时,只有函数间隔却是不够的
2.3 几何间隔
对于给定的训练数据集T和超平面(w,b),定义超平面(w,b)关于样本点\((x_i,y_i)\)的几何间隔为:$$\gamma{_i} = \frac{y_i(w\bullet{x_i} + b)}{||w||}$$
定义超平面(w,b)关于训练数据集T的几何间隔为超平面(w,b)关于T中所有样本点\((x_i,y_i)\)的几何间隔之最小值:$$\gamma = \min\limits_{i=1,...,N}\gamma_i$$
2.4 函数间隔和几何间隔之间的关系
从上面函数间隔和几何间隔的定义,可以得到函数间隔和几何间隔之间的关系:$$\gamma_i = \frac{\overline{\gamma_i}}{||w||}$$
2.5 硬间隔最大化分离超平面
支持向量机学习的基本想法是找到能够正确划分训练数据集并且几何间隔最大的分离超平面,换句话说也就是不仅将正负实例点分开,而且对最难分的实例点(离超平面最近的点)也有足够大的确信度将它们分开,硬间隔是与后面说明的软间隔相对应的
如何求得一个几何间隔最大化的分离超平面,可以表示为下面的约束优化问题:$$\max\limits_{w,b}\quad\gamma$$
根据上面函数间隔和几何间隔之间的关系,转换成下面的同等约束问题:$$\max\limits_{w,b}\quad\frac{\overline{\gamma}}{||w||}$$
由于当w,b按比例变换的的时候函数间隔\(\overline\gamma\)也会呈比例变化,先取\(\overline\gamma= 1\),再由于\(\frac{1}{||w||}\)最大化和最小化\(\frac{1}{2}{||w||}^2\)是等价的,于是得到:$$\min\limits_{w,b}\quad\frac{1}{2}{||w||^2}$$
由此得到分离超平面:$$w^{} \bullet x + b^{} = 0$$
分类决策函数:$$f(x) = sign(w^{} \bullet x + b^{})$$
求解拉格朗日对偶函数:$$L(w,b,a) = \frac{1}{2}{||w||}^2 - \sum_{i=1}^na_i[(y_i(x_iw+b)-1)]----(1)$$
对w求偏导:$$\frac{\partial L}{\partial w} = w - \sum_{i=1}^na_iy_ix_i = 0-----(2)$$
对b求偏导:$$\frac{\partial L}{\partial b} = \sum_{i=1}^na_iy_i = 0-------(3)$$
将(2)(3)带入(1)得到:$$maxL(a) = -\frac{1}{2}\sum_{i=1}n\sum_{j=1}na_ia_jy_iy_jx_ix_j + \sum_{i=1}^na_i$$
2.6 软间隔最大化分离超平面
对于线性可分的数据集可以直接使用硬间隔最大化超平面进行划分,但对于线性不可分的某些样本点不能满足函数间隔大于等于1的约束条件,为了解决这个问题,可以对每个样本点\((x_i,y_i)\)引进一个松弛变量\(\xi >= 0\),使函数间隔加上松弛变量大于等于1,这样约束条件变为:$$yi(w\bullet x_i + b) >= 1- \xi_{i}$$
同时,对每个松弛变量\(\xi_{i}\)支付一个代价\(\xi_{i},目标函数由原来的\)\(\frac{1}{2}{||w||}^2\)\(变为\)\(\frac{1}{2}{||w||}^2 + C\sum_{i=1}^n{\xi_i}\)
C为惩罚系数,一般由应用问题决定,C值大时对误分类的惩罚增大,C值小时对误分类惩罚小
线性不可分的线性支持向量机的学习问题编程如下凸二次规划问题:$$\min\limits_{w,b,\xi}\quad\frac{1}{2}{||w||^2}+ C\sum_{i=1}^n{\xi_i}$$
由此得到分离超平面:$$w^{} \bullet x + b^{} = 0$$
分类决策函数:$$f(x) = sign(w^{} \bullet x + b^{})$$
拉格朗日对偶函数:
2.7 支持向量和间隔边界
在线性可分的情况下,训练数据集的样本点中与分离超平面距离最近的样本点的示例称为支持向量,支持向量是使约束条件成立的点,即$$\quad\ y_i(w\bullet{x_i}+b) - 1 = 0$$或$$yi(w\bullet x_i + b) - (1- \xi_{i}) = 0$$,在\(y_i = +1\)的正例点,支持向量在超平面$$H_1:w^Tx + b = 1$$上,对\(y_i = -1\)的负例点,支持向量在超平面$$H_2:w^T x + b = -1$$上,此时\(H_1\)和\(H_2\)平行,并且没有实例点落在它们中间,在\(H_1\)和\(H_2\)之间形成一条长带,分离超平面与它们平行且位于它们中间,\(H_1和H_2\)之间的距离为间隔,间隔依赖于分割超平面的法向量\(w\),等于\(\frac{2}{|w|}\),\(H_1和H_2\)为间隔边界,如下图: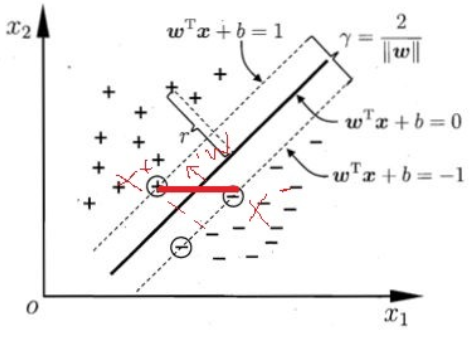
在决定分离超平面时只有支持向量起作用,而其他实例点并不起作用。如果移动支持向量将改变所求的解;但是如果在间隔边界以外移动其他实例点,甚至去掉这些点,则解是不会变的,由于支持向量在确定分离超平面中起着决定性的作用,所以将这种分类称为支持向量机。支持向量的个数一般很少,所以支持向量机由很少的‘很重要的’训练样本确定
3. 如何将线性不可分数据集转换为线性可分数据集
3.1 数据线性不可分的原因
(1) 数据集本身就是线性不可分隔的
(2) 数据集中存在噪声,或者人工对数据赋予分类标签出错等情况的原因导致数据集线性不可分
3.2 常用方法
将线性不可分数据集转换为线性可分数据集常用方法:
对于原因(2)
- 需要修正模型,加上惩罚系数C,修正后的模型,可以“容忍”模型错误分类的情况,并且通过惩罚系数的约束,使得模型错误分类的情况尽可能合理
对于原因(1)
- (1)通过相似函数添加相似特征
- (2)使用核函数(多项式核、高斯RBF核),将原本的低维特征空间映射到一个更高维的特征空间,从而使得数据集线性可分
3.3 核技巧在支持向量机中的应用
注意到在线性支持向量机的对偶问题中,无论是目标函数还是决策函数都只涉及输入实例与实例之间的内积,在对偶问题的目标函数中的内积\(x_ix_j\)可以用核函数$$K(x_i,x_j) = \phi (x_i)\bullet \phi(x_j)$$代替,此时对偶问题的目标函数成为$$maxL(a) = -\frac{1}{2}\sum_{i=1}n\sum_{j=1}na_ia_jy_iy_jK(x_i,x_j) + \sum_{i=1}^na_i$$
同样,分类决策函数中的内积也可以用核函数代替$$f(x) = sign(\sum_{i=1}na_iy_iK(x_i,x)+b^)$$
4 使用sklearn框架训练svm
- SVM特别适用于小型复杂数据集,samples < 100k
- 硬间隔分类有两个主要的问题:
- (1) 必须要线性可分
- (2) 对异常值特别敏感,会导致不能很好的泛化或无法找不出硬间隔
- 使用软间隔分类可以解决硬间隔分类的两个主要问题,尽可能保存街道宽敞和限制间隔违例(即位于街道之上,甚至在错误一边的实例)之间找到良好的平衡
- 在Sklean的SVM类中,可以通过超参数C来控制这个平衡,C值越小,则街道越宽,但是违例会越多,如果SVM模型过度拟合,可以试试通过降低C来进行正则化
4.1 线性可分LinearSVC类
4.1.1 LinearSVC类重要参数说明
- penalty: string,'l1'or'l2',default='l2'
- loss: string 'hing'or'squared_hinge',default='squared_hinge',hinge为标准的SVM损失函数
- dual: bool,defalut=True,wen n_samples > n_features,dual=False,SVM的原始问题和对偶问题二者解相同
- tol: float,deafult=le-4,用于提前停止标准
- C: float,defult=1.0,为松弛变量的惩罚系数
- multi_class: 默认为ovr,该参数不用修改
- 更多说明应查看源码
4.1.2 Hinge损失函数
函数max(0,1-t),当t>=1时,函数等于0,如果t<1,其导数为-1
def hinge(x):
if x >=1 :
return 0
else:
return 1-x
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-2,4,20)
y = [hinge(i) for i in x ]
ax = plt.subplot(111)
plt.ylim([-1,2])
ax.plot(x,y,'r-')
plt.text(0.5,1.5,r'f(t) = max(0,1-t)',fontsize=20)
plt.show()
<Figure size 640x480 with 1 Axes>
4.1.3 LinearSVC实例
from sklearn import datasets
import pandas as pd
iris = datasets.load_iris()
print(iris.keys())
print('labels:',iris['target_names'])
features,labels = iris['data'],iris['target']
print(features.shape,labels.shape)
# 分析数据集
print('-------feature_names:',iris['feature_names'])
iris_df = pd.DataFrame(features)
print('-------info:',iris_df.info())
print('--------descibe:',iris_df.describe())
dict_keys(['data', 'target', 'target_names', 'DESCR', 'feature_names', 'filename'])
labels: ['setosa' 'versicolor' 'virginica']
(150, 4) (150,)
-------feature_names: ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 150 entries, 0 to 149
Data columns (total 4 columns):
0 150 non-null float64
1 150 non-null float64
2 150 non-null float64
3 150 non-null float64
dtypes: float64(4)
memory usage: 4.8 KB
-------info: None
--------descibe: 0 1 2 3
count 150.000000 150.000000 150.000000 150.000000
mean 5.843333 3.057333 3.758000 1.199333
std 0.828066 0.435866 1.765298 0.762238
min 4.300000 2.000000 1.000000 0.100000
25% 5.100000 2.800000 1.600000 0.300000
50% 5.800000 3.000000 4.350000 1.300000
75% 6.400000 3.300000 5.100000 1.800000
max 7.900000 4.400000 6.900000 2.500000
# 数据进行预处理
from sklearn.preprocessing import StandardScaler,LabelEncoder
from sklearn.model_selection import RandomizedSearchCV
from sklearn.svm import LinearSVC
from scipy.stats import uniform
# 对数据进行标准化
scaler = StandardScaler()
X = scaler.fit_transform(features)
print(X.mean(axis=0))
print(X.std(axis=0))
# 对标签进行编码
encoder = LabelEncoder()
Y = encoder.fit_transform(labels)
# 调参
svc = LinearSVC(loss='hinge',dual=True)
param_distributions = {'C':uniform(0,10)}
rscv_clf =RandomizedSearchCV(estimator=svc, param_distributions=param_distributions,cv=3,n_iter=20,verbose=2)
rscv_clf.fit(X,Y)
print(rscv_clf.best_params_)
[-1.69031455e-15 -1.84297022e-15 -1.69864123e-15 -1.40924309e-15]
[1. 1. 1. 1.]
Fitting 3 folds for each of 20 candidates, totalling 60 fits
[CV] C=8.266733168092582 .............................................
[CV] .............................. C=8.266733168092582, total= 0.0s
[CV] C=8.266733168092582 .............................................
[CV] .............................. C=8.266733168092582, total= 0.0s
[CV] C=8.266733168092582 .............................................
[CV] .............................. C=8.266733168092582, total= 0.0s
[CV] C=8.140498369662586 .............................................
[CV] .............................. C=8.140498369662586, total= 0.0s
...
...
...
[CV] .............................. C=9.445168322251103, total= 0.0s
[CV] C=9.445168322251103 .............................................
[CV] .............................. C=9.445168322251103, total= 0.0s
[CV] C=2.100443613273717 .............................................
[CV] .............................. C=2.100443613273717, total= 0.0s
[CV] C=2.100443613273717 .............................................
[CV] .............................. C=2.100443613273717, total= 0.0s
[CV] C=2.100443613273717 .............................................
[CV] .............................. C=2.100443613273717, total= 0.0s
{'C': 3.2357870215300046}
# 模型评估
y_prab = rscv_clf.predict(X)
result = np.equal(y_prab,Y).astype(np.float32)
print('accuracy:',np.sum(result)/len(result))
accuracy: 0.9466666666666667
from sklearn.metrics import accuracy_score,precision_score,recall_score
print('accracy_score:',accuracy_score(y_prab,Y))
print('precision_score:',precision_score(y_prab,Y,average='micro'))
accracy_score: 0.9466666666666667
precision_score: 0.9466666666666667
5 附录
5.1 非线性SVM分类SVC
SVC类通过参数kernel的设置可以实现线性和非线性分类,具体参数说明和属性说明如下
5.1.1 SVC类参数说明
- C: 惩罚系数,float,default=1.0
- kernel: string,default='rbf',核函数选择,必须为('linear','poly','rbf','sigmoid','precomputed' or callable)其中一个
- degree: 只有当kernel='poly'时才有意义,表示多项式核的深度
- gamma: float,default='auto',核系数
- coef0,: float, optional (default=0.0),Independent term in kernel function,It is only significant in 'poly' and 'sigmoid',影响模型受高阶多项式还是低阶多项式影响的结果
- shrinking: bool,default=True
- probability: bool,default=False
- tol: 提前停止参数
- cache_size:
- class_weight: 类标签权重
- verbose: 日志输出类型
- max_iter: 最大迭代次数
- decision_function_shape: ‘ovo’,'ovr',defalut='ovr'
- random_state:
5.1.2 SVC类属性说明
- support_:
- support_vectors_:
- n_support_:
- dual_coef_:
- coef_:
- intercept_:
- fit_status_:
- probA_:
- probB_:
5.1.3 核函数选择
有这么多核函数,该如何决定使用哪一个呢?有一个经验法则是,永远先从线性核函数开始尝试(LinearSVC比SVC(kernel='linear')快的多),特别是训练集非常大或特征非常多的时候,如果训练集不太大,可以试试高斯RBF核,大多数情况下它都非常好用。如果有多余时间和精力,可以使用交叉验证核网格搜索来尝试一些其他的核函数,特别是那些专门针对你数据集数据结构的和函数
5.2 GridSearchCV类说明
5.2.1 GridSearchCV参数说明
- estimator: 估算器,继承于BaseEstimator
- param_grid: dict,键为参数名,值为该参数需要测试值选项
- scoring: default=None
- fit_params:
- n_jobs: 设置要并行运行的作业数,取值为None或1,None表示1 job,1表示all processors,default=None
- cv: 交叉验证的策略数,None或integer,None表示默认3-fold, integer指定“(分层)KFold”中的折叠数
- verbose: 输出日志类型
5.2.2 GridSearchCV属性说明
- cv_results_: dict of numpy(masked) ndarray
- best_estimator_:
- best_score_: Mean cross-validated score of the best_estimator
- best_params_:
- best_index_: int,The index (of the ``cv_results_`` arrays) which corresponds to the best candidate parameter setting
- scorer_:
- n_splits_: The number of cross-validation splits (folds/iterations)
- refit_time: float
5.3 RandomizedSearchCV类说明
5.3.1 RandomizedSearchCV参数说明
- estimator: 估算器,继承于BaseEstimator
- param_distributions: dict,键为参数名,Dictionary with parameters names (string) as keys and distributions or lists of parameters to try. Distributions must provide a ``rvs`` method for sampling (such as those from scipy.stats.distributions). If a list is given, it is sampled uniformly
- n_iter: 采样次数,default=10
- scoring: default=None
- fit_params:
- n_jobs: 设置要并行运行的作业数,取值为None或1,None表示1 job,1表示all processors,default=None
- cv: 交叉验证的策略数,None或integer,None表示默认3-fold, integer指定“(分层)KFold”中的折叠数
- verbose: 输出日志类型
5.3.2 RandomizedSearchCV属性说明
- cv_results_: dict of numpy(masked) ndarray
- best_estimators_:
- best_score_: Mean cross-validated score of the best_estimator
- best_params_:
- best_index_: int,The index (of the ``cv_results_`` arrays) which corresponds to the best candidate parameter setting
- scorer_:
- n_splits_: The number of cross-validation splits (folds/iterations)
- refit_time: float
参考资料:
- (1)<机器学习实战基于Scikit-Learn和TensorFlow>
- (2)<百面机器学习>
- (3)李航<统计学习方法>
- (4)https://zhuanlan.zhihu.com/p/21932911?refer=baina


