机器学习之数据分析
熟话说,'巧妇难为无米之炊',数据和特征就是'米',模型和算法则是'巧妇',没有充足的数据、合适的特征,再强大的模型结构也无法得到满意的输出,为了更好的使用模型,必须先对数据有个正确的认识,本博将对数据分析的三种方法(描述性统计,数据可视化和相关性系数)进行总结,为数据预处理准备
1. sklearn数据集类型
- 自带的小数据集:sklearn.datasets.load_<name>
鸢尾花数据集:load_iris()
乳腺癌数据集:load_breast_cancer()
手写数字集:load_digits()
- 可在线下载的数据集:sklearn.datasets.fetch_<name>
- 计算机生成的数据集:sklearn.datasets.make_<name>
- svmlight/libsvm格式的数据集:sklearn.datasets.load_svmlight_file()
- 从买了data.org在线下载获取数据集:sklearn.datasets.fetch_mldata()
2. 数据分析
下面将以房价数据为例进行说明这个数据分析过程
2.1 获取数据
import pandas as pd
housing = pd.read_csv('./datasets/housing/housing.csv')
2.2 查看列标信息
print(housing.columns)
Index(['longitude', 'latitude', 'housing_median_age', 'total_rooms',
'total_bedrooms', 'population', 'households', 'median_income',
'median_house_value', 'ocean_proximity'],
dtype='object')
2.3 查看数据集前5行信息
print(housing.head())
longitude latitude housing_median_age total_rooms total_bedrooms \
0 -122.23 37.88 41.0 880.0 129.0
1 -122.22 37.86 21.0 7099.0 1106.0
2 -122.24 37.85 52.0 1467.0 190.0
3 -122.25 37.85 52.0 1274.0 235.0
4 -122.25 37.85 52.0 1627.0 280.0
population households median_income median_house_value ocean_proximity
0 322.0 126.0 8.3252 452600.0 NEAR BAY
1 2401.0 1138.0 8.3014 358500.0 NEAR BAY
2 496.0 177.0 7.2574 352100.0 NEAR BAY
3 558.0 219.0 5.6431 341300.0 NEAR BAY
4 565.0 259.0 3.8462 342200.0 NEAR BAY
2.4 获取数据集的简单描述
print(housing.info())
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 20640 entries, 0 to 20639
Data columns (total 10 columns):
longitude 20640 non-null float64
latitude 20640 non-null float64
housing_median_age 20640 non-null float64
total_rooms 20640 non-null float64
total_bedrooms 20433 non-null float64
population 20640 non-null float64
households 20640 non-null float64
median_income 20640 non-null float64
median_house_value 20640 non-null float64
ocean_proximity 20640 non-null object
dtypes: float64(9), object(1)
memory usage: 1.6+ MB
None
注意:total_bedrooms这个属性只有20433个非空值,这意味着又207个区域缺失这个特征,所有的属性的字段都是float,除了ocean_proximity,它的类型是object,因此它可以是任何类型的Python对象
2.5 查看分类标签种类和数量
print(housing['ocean_proximity'].value_counts()) #查看属性类别
<1H OCEAN 9136
INLAND 6551
NEAR OCEAN 2658
NEAR BAY 2290
ISLAND 5
Name: ocean_proximity, dtype: int64
2.6 查看数据集统计描述信息
print(housing.describe()) #查看描述性信息
longitude latitude housing_median_age total_rooms \
count 20640.000000 20640.000000 20640.000000 20640.000000
mean -119.569704 35.631861 28.639486 2635.763081
std 2.003532 2.135952 12.585558 2181.615252
min -124.350000 32.540000 1.000000 2.000000
25% -121.800000 33.930000 18.000000 1447.750000
50% -118.490000 34.260000 29.000000 2127.000000
75% -118.010000 37.710000 37.000000 3148.000000
max -114.310000 41.950000 52.000000 39320.000000
total_bedrooms population households median_income \
count 20433.000000 20640.000000 20640.000000 20640.000000
mean 537.870553 1425.476744 499.539680 3.870671
std 421.385070 1132.462122 382.329753 1.899822
min 1.000000 3.000000 1.000000 0.499900
25% 296.000000 787.000000 280.000000 2.563400
50% 435.000000 1166.000000 409.000000 3.534800
75% 647.000000 1725.000000 605.000000 4.743250
max 6445.000000 35682.000000 6082.000000 15.000100
median_house_value
count 20640.000000
mean 206855.816909
std 115395.615874
min 14999.000000
25% 119600.000000
50% 179700.000000
75% 264725.000000
max 500001.000000
3. 数据可视化
数据可视化可以通过各种图表显示,如直方图、点图、箱体图、QQ图,下面以longitude属性为例
3.1 点图
import matplotlib.pyplot as plt
plt.plot(housing.index,housing['longitude'],'r.')
plt.show()
3.2 绘制直方图
plt.hist(housing['longitude'],bins=20)
plt.show()
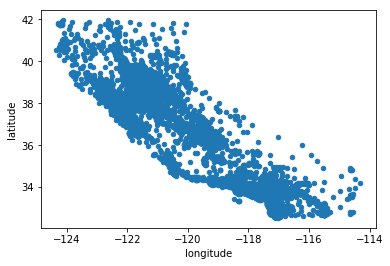
3.3 将地理数据可视化
housing.plot(kind='scatter',x='longitude',y='latitude')
<matplotlib.axes._subplots.AxesSubplot at 0x206138f5fd0>
housing.plot(kind='scatter',x='longitude',y='latitude',alpha=0.1)
<matplotlib.axes._subplots.AxesSubplot at 0x2061395bc88>
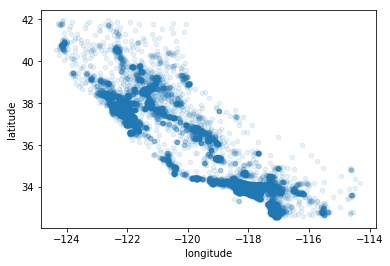
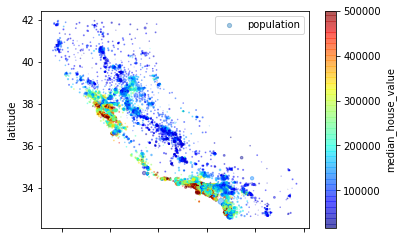
接下来看看房价,每个圆的半径大小代表了每个地区的人口数量(选项s),颜色代表价格(选项c),使用jet的预定义颜色表(选项cmap)来进行可视化,颜色范围从蓝到红(从低到高)
housing.plot(kind='scatter',x='longitude',y='latitude',alpha=0.4,s=housing['population']/1000,
label='population',c='median_house_value',cmap=plt.get_cmap('jet'),colorbar=True)
plt.legend()
<matplotlib.legend.Legend at 0x206139bdc88>
4 查看特征相关性
由于数据集不大,可以使用corr()轻松计算除每队属性之间标准相关系数,也称为皮尔逊相关系数
皮尔逊相关系数公式:
计算相关性系数时还可以使用欧式距离和余弦相似度,但需要明确它们的使用场景,欧式距离主要关注数值之间的差异,当相对于平均水平偏离度很大时,不能很好的反映真实的相似度,余弦相似度更偏重于维度之间的差异
corr_matrix = housing.corr()
print(corr_matrix['median_house_value'].sort_values(ascending=False))
median_house_value 1.000000
median_income 0.688075
total_rooms 0.134153
housing_median_age 0.105623
households 0.065843
total_bedrooms 0.049686
population -0.024650
longitude -0.045967
latitude -0.144160
Name: median_house_value, dtype: float64
相关系数的范围从-1变换到1,越接近1,表示越强的正相关,越接近-1,表示越强烈的负相关,系数靠近0时说明二者之间没有线性相关性。
\({\color {red} {注意,相关系数仅测量线性相关性,所以它有可能彻底遗漏非线性相关性}}\)
附:变异值度量
极差
极差 = 最大值 - 最小值
样本方差
n个测量值\(x_1,x_2,...,x_n\)的样本方差定义为$$s^2 = \frac{1}{n-1}\sum_{i=1}^n{(x_i - \mu)}^2$$
注意:有偏方差和无偏方差的区别
标准方差
解释标准差的两个有效法则:经验法和切比雪夫法则
经验法则
若一个数据集有近似丘形的对称分布,则可以用以下的经验法则描述数据集
(1)大约68%的测量值位于均值的1个标准差范围内(\(即对于样本在区间\mu\pm s范围内,对于总体在区间\mu\pm \sigma范围内)\)
(2)大约95%的测量值位于均值的2个标准差范围内(\(即对于样本在区间\mu\pm 2s范围内,对于总体在区间\mu\pm 2\sigma范围内)\)
(3)几乎所有测量值位于均值的2个标准差范围内(\(即对于样本在区间\mu\pm 3s范围内,对于总体在区间\mu\pm 3\sigma范围内)\)
切比雪夫法则
对于任一数据集,无论数据的频数是什么形状
(1)可能很少的测量值落在均值的1个标准差范围内(\(即对于样本在区间\mu\pm s范围内,对于总体在区间\mu\pm \sigma范围内)\)
(2)至少有\(\frac{3}{4}\)的测量值落在均值的2个标准差范围内(\(即对于样本在区间\mu\pm 2s范围内,对于总体在区间\mu\pm 2\sigma范围内)\)
(3)至少有\(\frac{8}{9}\)的测量值落在均值的3个标准差范围内(\(即对于样本在区间\mu\pm 3s范围内,对于总体在区间\mu\pm 3\sigma范围内)\)
(4)通常,对于任意大于1的数k,至少有\(1-\frac{1}{k^2}\)的测量值落在均值的k个标准差范围内


