机器学习之K均值聚类
K均值聚类思想
聚类的核心概念是相似度或距离,有很多相似度或距离的方法,比如欧式距离、马氏距离、相关系数、余弦定理、层次聚类和K均值聚类等
K均值聚类的基本思想是,通过迭代的方法寻找K个簇的一种划分方案,使得聚类结果对应的代价函数最小,特别地,代价函数可以定义为各个样本距离所属簇中心点的误差平方和$$J(c,\sigma) = \sum_{i=1}^M{||x_i - \sigma_{c_i}||}^2$$
其中\(x_i\)代表第i个样本点,\(c_i\)是\(x_i\)所属于的簇,\(\sigma_{c_i}\)代表簇对应的中心点,M是样本总数
K-Mean_Cluster算法实现
使用'/datasets/kmeansTestSet.txt'数据集测试K均值聚类算法
def loadDataset(file):
dataset = []
with open(file,'r') as pf:
for line in pf:
dataset.append([float(x) for x in line.strip().split('\t')])
return dataset
#加载数据
dataset = loadDataset('./datasets/kmeansTestSet.txt')
print(len(dataset))
print(dataset[:5])
80
[[1.658985, 4.285136], [-3.453687, 3.424321], [4.838138, -1.151539], [-5.379713, -3.362104], [0.972564, 2.924086]]
import numpy as np
#对数据进行归一化处理
def normalize(dataset):
dataMat = np.mat(dataset)
mean = np.mean(dataMat)
var = np.var(dataMat)
meanDataMat = (dataMat - mean) / var #将数据进行归一化处理
return meanDataMat
import matplotlib.pyplot as plt
import pandas as pd
#以图形方式展现数据
def plotDataset(meanDataMat,pointCenter = False,centerPointerMat=None):
dataFrame = pd.DataFrame(meanDataMat) #转换为DataFrame,方便查看数据属性
print(dataFrame.describe())
#plt.axis([0,1,0,1])
plt.plot(meanDataMat[:,0],meanDataMat[:,1],'r*')
if pointCenter:
plt.plot(centerPointerMat[:,0],centerPointerMat[:,1],'b*')
plt.show()
meanDataMat = normalize(dataset)
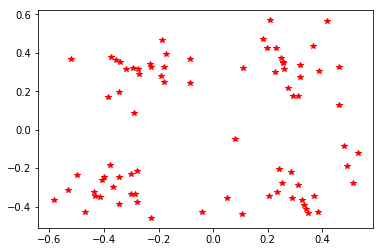
plotDataset(meanDataMat)
0 1
count 80.000000 80.000000
mean -0.008614 0.008614
std 0.331392 0.333145
min -0.584224 -0.459075
25% -0.306803 -0.325977
50% 0.005867 0.019362
75% 0.290189 0.323504
max 0.530519 0.568950
def distance(vectA,vectB):
Power = np.power((vectA - vectB),2)
Sum = np.sum(Power,axis = 1)
return float(np.sqrt(Sum))
import random
def kcluster(meanDataMat,k=4):
row,col = meanDataMat.shape
print(row,col)
featureRange = []
for i in range(col):
Min = np.min(meanDataMat[:,i])
Max = np.max(meanDataMat[:,i])
featureRange.append((Min,Max))
centerPoints = [] #中心点
classPoints = [] #聚类数据点
classLabels = np.mat(np.zeros((row,2)))
for i in range(k):
centerPoints.append([random.uniform(r[0],r[1]) for r in featureRange])
classPoints.append([])
centerPointsMat = np.mat(centerPoints)
clusterChanged = True
while(clusterChanged):
clusterChanged = False
for i in range(row):
minDis = np.inf
bestK = -1
for j in range(k):
dis = distance(meanDataMat[i,:],centerPointsMat[j,:])
if dis < minDis:
minDis = dis
bestK = j
if classLabels[i,0] != bestK:
clusterChanged = True
classLabels[i,:] = bestK,minDis
for center in range(k):
ptsInClust = meanDataMat[np.nonzero(classLabels[:,0] == center)[0]] #该步骤需要特别注意,精妙
centerPointsMat[center,:] = np.mean(ptsInClust,axis=0)
print('已完成聚类')
return centerPointsMat,classLabels
centerPointsMat,classLabels = kcluster(meanDataMat)
80 2
已完成聚类
plotDataset(meanDataMat,pointCenter=True,centerPointerMat = centerPointsMat)
0 1
count 80.000000 80.000000
mean -0.008614 0.008614
std 0.331392 0.333145
min -0.584224 -0.459075
25% -0.306803 -0.325977
50% 0.005867 0.019362
75% 0.290189 0.323504
max 0.530519 0.568950
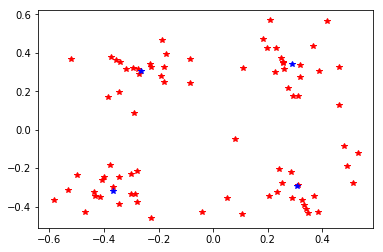
K均值算法的缺点
(1)需要人工预先确定初始值K值,且该值和真实的数据分布未必吻合
(2)K均值只能收敛到局部最优,效果受到初始值的影响
(3)易受噪点和离群点的影响
(4)样本点只能被划分到单一的类中
K均值聚类算法改进模型
K-means++算法
K均值的改进算法种,对初始值选择的改进种是很重要的一部分,而这类算法中,最具影响力的当属K-means++算法,原始K均值算法最开始随机的选取K个中心点,而K-means++按照如下的思想选取K个聚类中心:
假设已经选取了n个初始聚类中心(0<n<k),则在选取第n+1个聚类中心时,距离当前n个聚类中心越远的点会有更高的概率被选为第n+1个聚类中心点。聚类中心点当然是相互离的越远越好。当选择完初始点后K-means++后续的执行和经典K均值算法相同
ISODATA算法
在K均值算法种,聚类个数K的值需要预先认为确定,并且在整个算法过程种无法改变,而当遇到高维度、海量的数据集时,人们往往很难准确地估计出K的大小,ISODATA的全称为迭代自组织数据分析法,就是针对这个问题进行了改进,它的思想很直观,主要通过迭代的方法对分类进行拆分和合并,这需要制定3个阈值:
(1)每个类所要求的最少样本数目\(N_min\),如果分裂后会导致某个子类别所包含样本数目小于该阈值,就不会对该类别进行分裂操作
(2)最大方差Sigma,用于控制某个类别中样本的分散程度,当样本的分散程度超过某个阈值时,进行分裂操作
(3)两个聚类中心之间所允许的最小距离\(D_min\),如果两个类考的非常近(即这两个类别对应聚类中心之间距离非常小),小于该阈值时,则对这两个类进行合并操作


