机器学习之K-近邻算法
1. 橙子还是柚子
该例子来自于《算法图解》,看下图中的水果是橙子还是柚子?
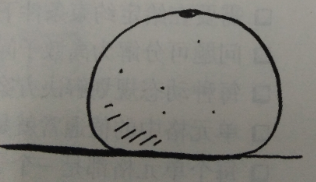
我的思维过程类似于这样:我脑子里面有个图表
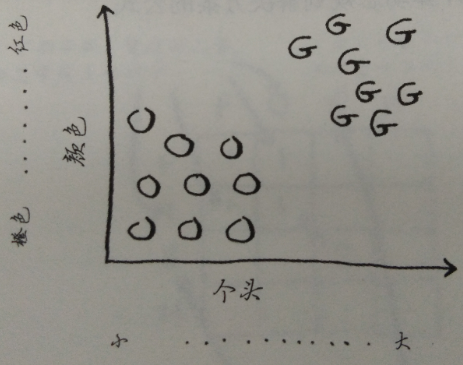
图中左下的表示橙子,右上的表示柚子,取橙子和柚子的两个特征(大和红),一般而言,柚子更大、更红,上图的水果又大又红,因此可能是柚子,那下面的水果呢?
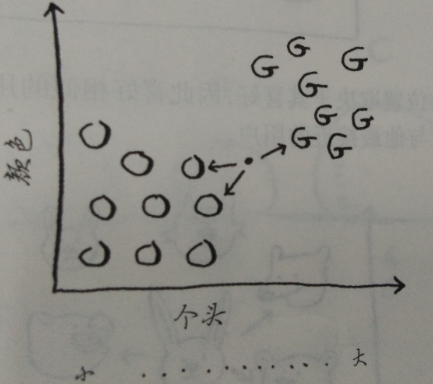
一种办法是看它的邻居,离它最近的邻居的三个邻居中有两个橙子一个柚子,因此这个水果很可能是橙子
上面刚使用的方法就是KNN(K-近邻算法),感觉是不是很简单
2. K-近邻算法步骤
对未知类别属性的数据集中的每个点依次执行以下操作:
(1)计算已知类别数据集中的点与当前点之间的距离
(2)按照距离递增顺序排序
(3)选取与当前点距离最小的K个点
(4)确定前k个点所在类别的出现频率
(5)返回前k个点出现频率最高的类别作为当前点的预测分类
3. K-近邻算法实现
使用Python按照上面的步骤实现算法
import numpy as np def knn(labels, dataset, in_data,k): """ labels:list dataset:ndarray in_data:ndarray k:int """ row = dataset.shape[0] sub_set = dataset - np.tile(in_data,(row,1)) sqrt_set = sub_set ** 2 distance = sqrt_set.sum(axis=1) ** 0.5 dic = {} sortedIndex_list = distance.argsort() # 算出邻居中对应的label次数 result = {} for i in range(k): key = sortedIndex_list[i] result[labels[key]] = result.get(labels[key],0)+1 result_list=sorted(result.items(), key=lambda x: x[1],reverse=True) return result_list[0][0]
4. 示例1:约会匹配
需求:
根据数据特征值(玩游戏所耗时间百分比、每年获得的飞行里程数、每周消费的冰淇淋公升数),判断对该约会对象的喜好程度,绝对是否要去约会
准备工作:
(1)数据集:dataset\datingTestSet2.txt
(2)数据集特征:
a. 玩游戏所耗时间百分比 ---->数据集中的第一列
b. 每年获得的飞行里程数 ---->数据集中的第二列
c. 每周消费的冰淇淋公升数 ---->数据集中的第三列
(3)样本分类标签:---->数据集中的第四列
(4)测试数据集:dataset\datingTestSet.txt
实现:
(1)从文件提取数据集和标签
def file2matrix(filename): """将文件数据转换为numpy.ndarray""" list_lines = [] with open(filename,'r') as pf: lines = pf.readlines() for line in lines: list_lines.append([float(i) for i in line.strip().split('\t')]) matrix = np.array(list_lines) data_set = matrix[:,0:-1] class_labels = matrix[:,-1:] class_labels = class_labels.reshape(1,1000).tolist()[0] return data_set,class_labels
(2)对数据集中的特征值数据进行归一化处理
def auto_norm(dataset): """ 为了防止各特征值之间的数值差距太大而影响计算结果, 对矩阵数据进行归一化处理,将每个特征值都转换为[0,1] """ min = dataset.min(0) max = dataset.max(0) sub = max - min norm_dataset = np.zeros(dataset.shape) row = dataset.shape[0] norm_dataset = dataset - np.tile(min,(row,1)) norm_dataset = norm_dataset / np.tile(sub,(row,1)) return norm_dataset,sub,min
(3)使用测试数据集对算法进行测试
def test_datingTestSet(): data_set,date_labels = file2matrix('dataset\\datingTestSet2.txt') norm_dataset,sub,min = auto_norm(data_set) #根据数据集测试KNN算法的正确率 rows = norm_dataset.shape[0] ok = 0 for i in range(rows): result = knn(date_labels,norm_dataset,norm_dataset[i,:],3) if result == date_labels[i]: ok += 1 else: print("测试错误结果为{},正确结果为{}".format(result, date_labels[i])) print("测试总记录数为{},成功记录数为{},KNN算法成功率为{}".format(rows,ok,ok/rows))
输出:

5. 示例2:手写识别系统
需求:
根据dataset\trainingDigits文件夹中的样本数据和dataset\testDigits文件夹中的样本数据测试KNN算法
实现:
(1)将每个文件中的数据(32*32)转换为matrix(m*1024)
def imgae2matrix(filepath): filelist = os.listdir(filepath) m = len(filelist) array_m_1024 = np.zeros((m,1024)) k = 0 labels = [] for file in filelist: #对文件名进行处理得到labels label = file.split('_')[0] labels.append(label) array_1_1024 = np.zeros((1,1024)) with open(os.path.join(filepath,file),'r') as pf: for i in range(32): line = pf.readline() for j in range(32): array_1_1024[0,32*i+j] = int(line[j]) array_m_1024[k,:] = array_1_1024 k+=1 return array_m_1024,labels
(2)使用knn算法测试成功率
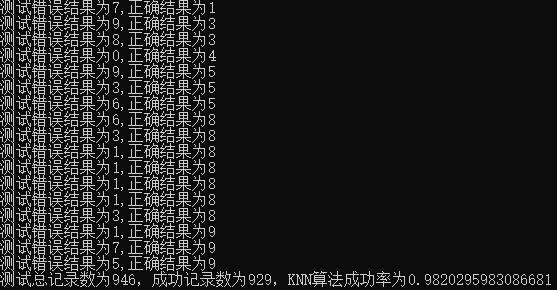
def test_numbers(): array_m_1024,labels = imgae2matrix('dataset\\trainingDigits\\') test_array_m_1024,test_labels = imgae2matrix('dataset\\testDigits\\') ok = 0 rows = test_array_m_1024.shape[0] for i in range(rows): in_data = test_array_m_1024[i,:] result = knn(labels, array_m_1024, in_data,5) if result == test_labels[i]: ok += 1 else: print("测试错误结果为{},正确结果为{}".format(result, test_labels[i])) print("测试总记录数为{},成功记录数为{},KNN算法成功率为{}".format(rows,ok,ok/rows))
(3)输出
6. 总结
K-近邻算法是分类数据最简单有效的算法,使用算法时必须有接近实际数据的训练样本数据,如果训练数据集很大,必须使用大量的存储空间,此外由于必须对数据集中的每个数据计算距离值,实际使用时可能非常耗时。
K-近邻算法的另一个缺陷是它无法给出任何数据的基础结构信息,因此我们也无法知晓平均实例样本和典型实例样本具有什么特征。
代码和数据集都已上传至:https://github.com/lizoo6zhi/MachineLearn.samples


