深度学习笔记

简单概念

1、Top-1,Top-5

Top-1就是指第一种类别上的精确度或者错误率(在这张图片中是错误率)，Top-5指的是前五种类别的总错误率。

2、train_data.batch(128):

从数据集中抽取128个样本

3、train_data.buffle(5000):

从数据集中按顺序抽取5000个样本放在buffer中，然后打乱buffer中的样本

4、深度网络结构存在的问题

• 参数太多，如果训练数据集有限，很容易产生过拟合
• 网络越大、参数越多，计算复杂性越大，难以应用
• 网络越深，容易出现梯度弥散问题（梯度越往后穿越越容易消失），难以优化模型

5、过拟合

过拟合表示神经网络在训练集上的表现很好，但是泛化能力比较差，在测试集上表现不好

6、KL散度

判断两个概率分布是否相等

7、enumerate函数

用于遍历数据对象（如列表，数组，元祖，字符串）

8、softmax函数

将输入的数据转换成他们各自所对应的概率值

9、layers.Dense(3)

3是神经元的个数

10、vscode代码编写

10.1 notebook运行乱码

使用vscode进行编写jupyter notebook代码编写时，如果要运行!dir查看当前目录下的文件及文件夹时，可能会出现如下乱码：

此时只需要在命令前面加上如下命令，即可解决该问题

11、tf2.1中的改动

11.1 SavedModel方式保存模型

tf.keras.experimental.export_saved_model(network, path)这种方式已经不能用了，需要替换成如下代码

tf.keras.models.save_model(model,'saved_model')

同样加载模型代码也随之改变，network = tf.keras.experimental.load_from_saved_model('model-savedmodel')这种方式执行同样会报错，需要替换成：

model=tf.keras.models.load_model('saved_model')

12、常见的网络层类

• 全连接层
• 激活函数层
• 池化层
• 卷积层
• 循环神经网络层等

13、matplotlib

13.1 plt.imshow

plt.imshow(X, interpolation=None)

• X：图像数据
  • (M, N)：标量数据的图像，灰度图
  • (M, N, 3)：RGB图像
  • (M, N, 4)：RGBA图像
• cmap:颜色图谱

13.2 plt.subplot

subplot(nrows, ncols, plot_number)

subplot(nrows, ncols, plot_number)

• nrows：子图的行数
• ncols：子图的列数
• plot_number 索引值，表示把图画在第plot_number个位置（从左下角到右上角）

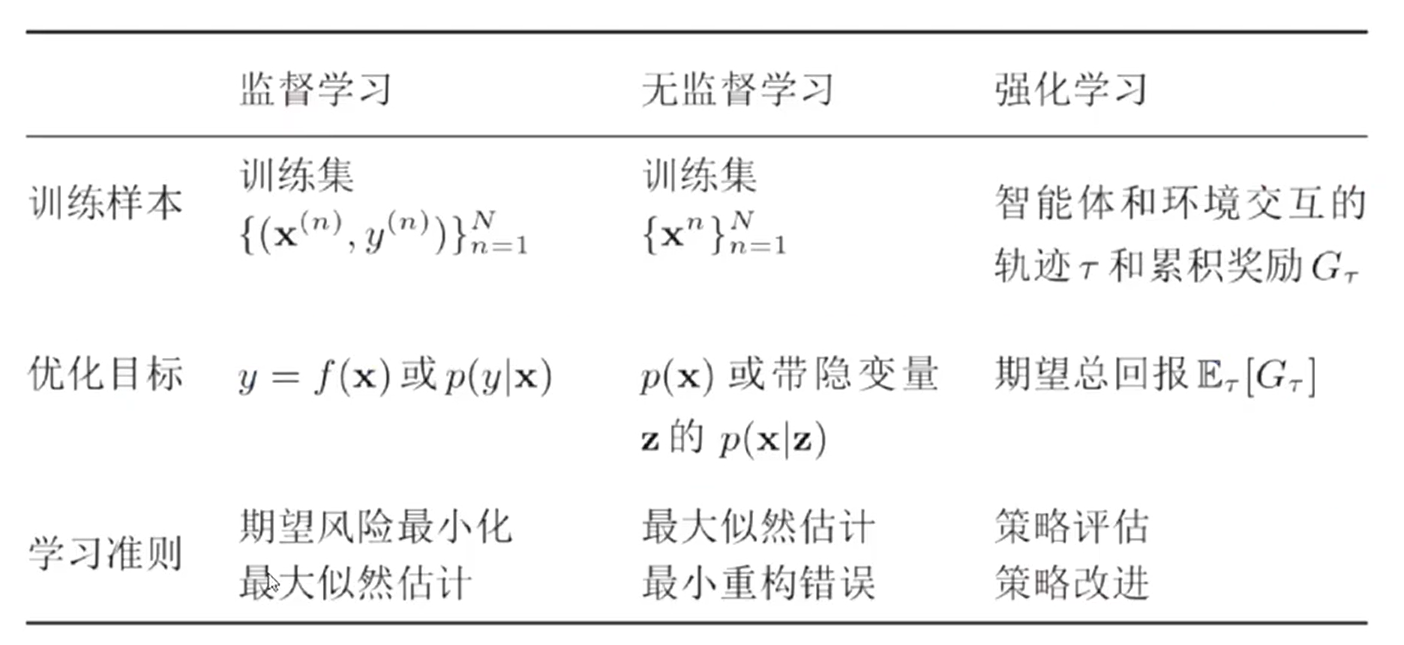
一、机器学习

1、基本概念

• 样本、特征、标签、模型、算法等

• 许多个样本构成数据集

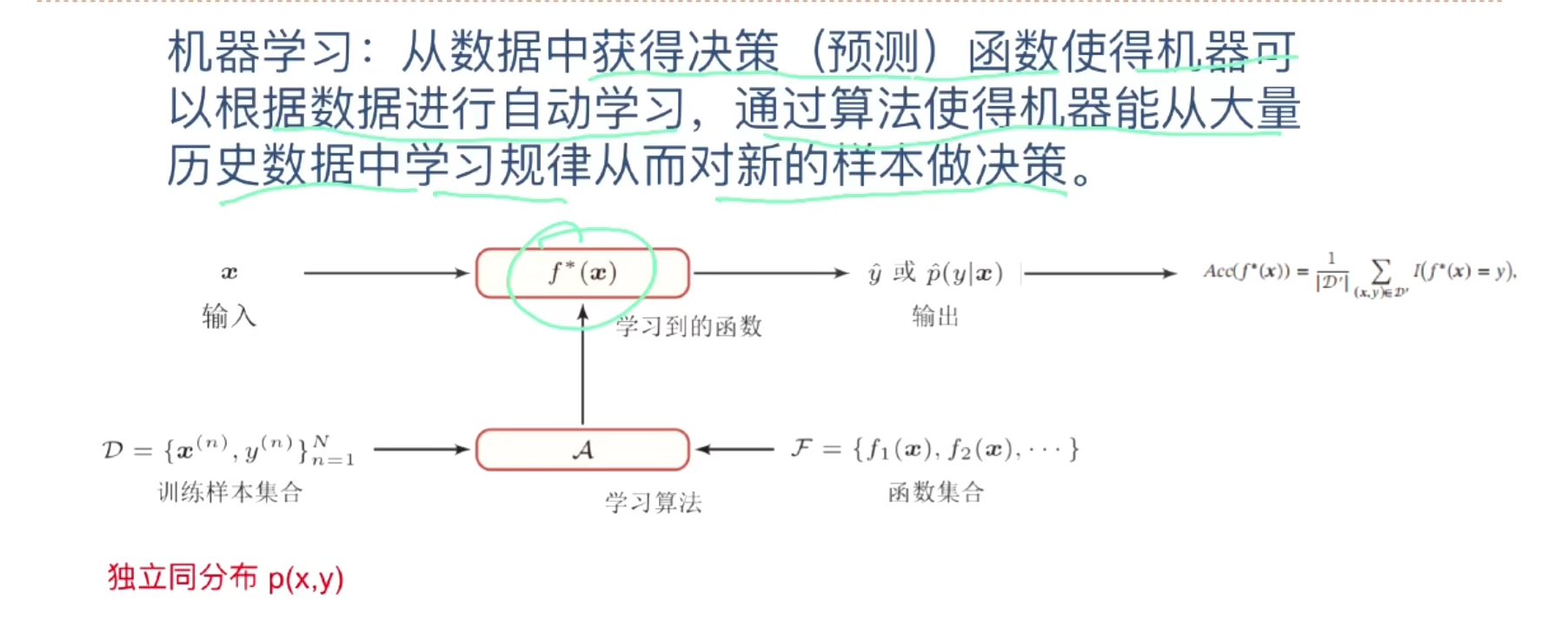
2、三要素

• 模型

• 学习准则之损失函数

  • 多分类

    • 交叉熵损失函数

    • 0-1损失函数

    • 平方损失函数

      

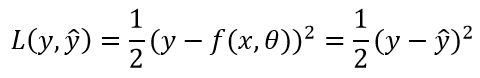
    • 绝对值损失函数

  • 二分类

    Hinge损失函数

• 优化算法

  过拟合、减少泛化错误、正则化

  • 梯度下降法

    • 批量梯度下降发

    • 随机梯度下降法（BGD）

      

      实战，写代码（已做）

    • 小批量随机梯度下降法

3、线性回归

模型

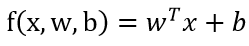
• 增广权重向量

• 增广特征向量

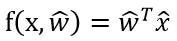
w的增广包含w和b，x的增广包含x和1

优化方法--参数学习

• 经验风险最下化（最小二乘法，最小均方误差算法）----（实数）LMS

  • 模型

  

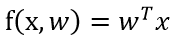
  • 学习准则

    平方损失函数

    

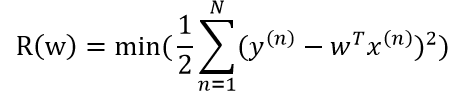
    特征之间独立同分布

• 结构风险最下化（岭回归）----（实数）

• 最大似然估计----（概率）

• 最大后验估计----（概率）

最小二乘法求一元线性回归实战

np.random.normal(size=(100,1),scale=1)

• 这是的np是numpy包的缩写，np.random.normal()的意思是一个正态分布，normal这里是正态的意思。一个例子：numpy.random.normal(loc=0,scale=1e-2,size=shape) ，意义如下：

1. 参数loc(float)：正态分布的均值，对应着这个分布的中心。loc=0说明这一个以Y轴为对称轴的正态分布，
2. 参数scale(float)：正态分布的标准差，对应分布的宽度，scale越大，正态分布的曲线越矮胖，scale越小，曲线越高瘦。
3. 参数size(int 或者整数元组)：输出的值赋在shape里，默认为None。

4、偏差与方差

• 如何选择一个合适的模型？

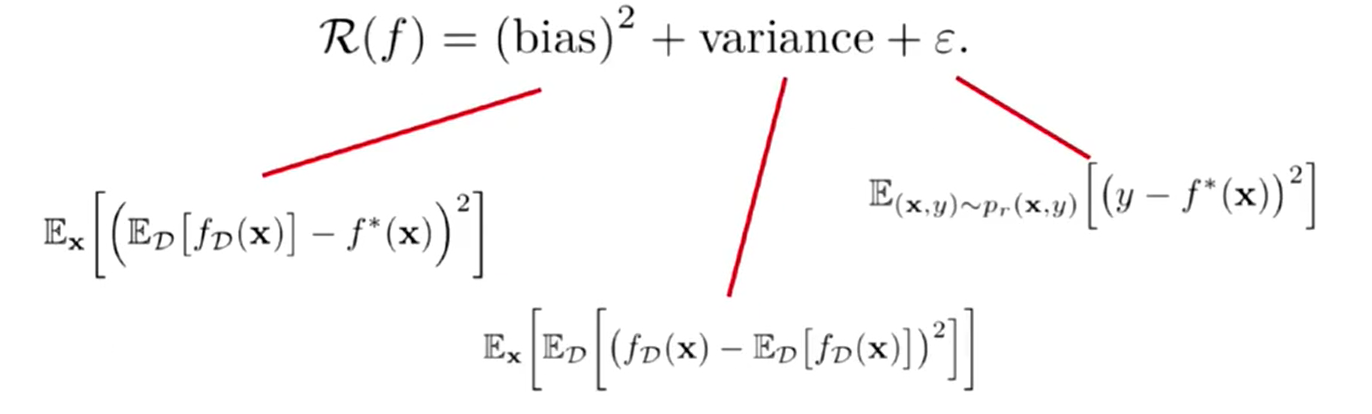
R(f):期望错误

bias:偏差

variance:方差

第四个参数：常数

• 模型选择：偏差与方差

  • 高偏差是训练集和测试集表现都不好，高方差是训练集表现好，测试集表现不好

  • 选择相对较好的模型的顺序：方差小，偏差小 > 方差小，偏差大 > 方差大，偏差小 > 方差大，偏差大。

• 集成模型：有效的将地方差的方法

• 常见的机器学习

• 常用的评价指标

  • 准确率
  • 错误率
  • 查准率（TP,TN,FP,FN）
  • 查全率
  • F值
  • 宏平均和微平均
  • AUC曲线
  • ROC曲线
  • PR曲线
  • 交叉验证（K折交叉验证）

二、线性模型

1、偏差与方差

2、数据集

• 图片 CIFAR-10

• 图片 ImageNet

• 应用

  • 图像分类
  • 文本情感分类
  • 垃圾邮件过滤
  • 文档归类

3、分类问题中的线性模型

• 线性回归

  通过样本特征的线性组合来进行预测的模型

• Logistic回归（Logistic Regression）

• Softmax回归（Softmax Regression）

• 感知器（Perceptron）

• 支持向量机（SVM）

4、从概率的角度看待分类问题

5、学习准则

• 交叉熵

在信息论中，熵用来衡量一个随机时间的不确定性

交叉熵是按照概率分布q的最优编码对真实分布为p的信息进行编码的长度。

事件发生的概率越大，信息量越小

​

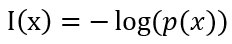
6、逻辑回归参数问题

• 梯度下降

  交叉熵损失函数，模型在训练集的风险函数为：

  

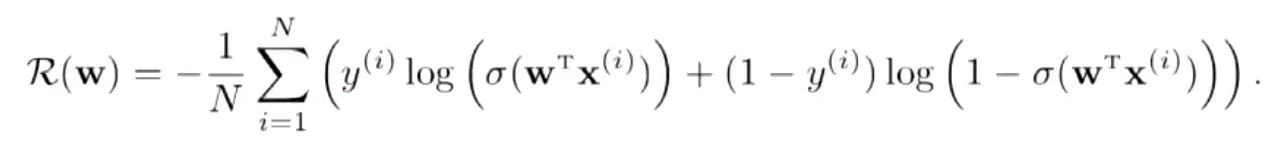
  梯度为

  

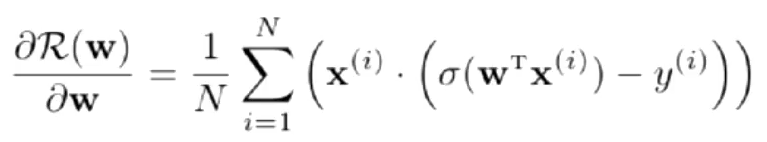
  其中 ：

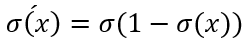
参数更新

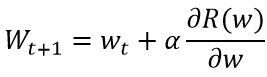
• 实战

  np.mean:求均值

7、Softmax回归

是logistic回归的多类推广（二分类）

wc表示第c类的权重向量

多分类

• 模型：Softmax回归

• 学习准则：交叉熵

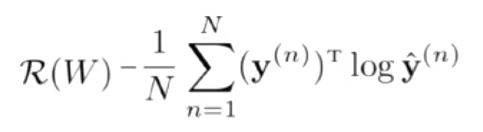
• 优化：梯度下降

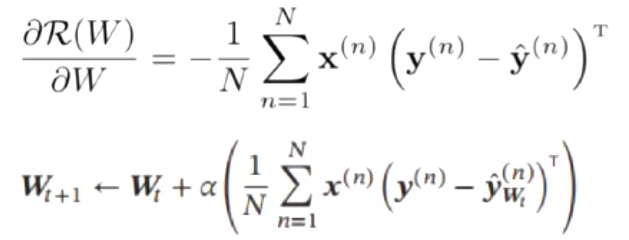
• 实战

  • numpy.unqiue函数接受一个数组，去除其中重复元素，并按元素由大到小返回一个新的无元素重复的元组或者列表
  • one_hot编码差不多搞懂

8、感知器

错误驱动的学习算法

• 感知器的学习过程

5.9 作业：使用softmax回归进行MNIST数据集的手写数字识别

三、前馈神经网络

神经网络是一种大规模的并行分布式处理器，天然具有存储并使用经验知识的能力

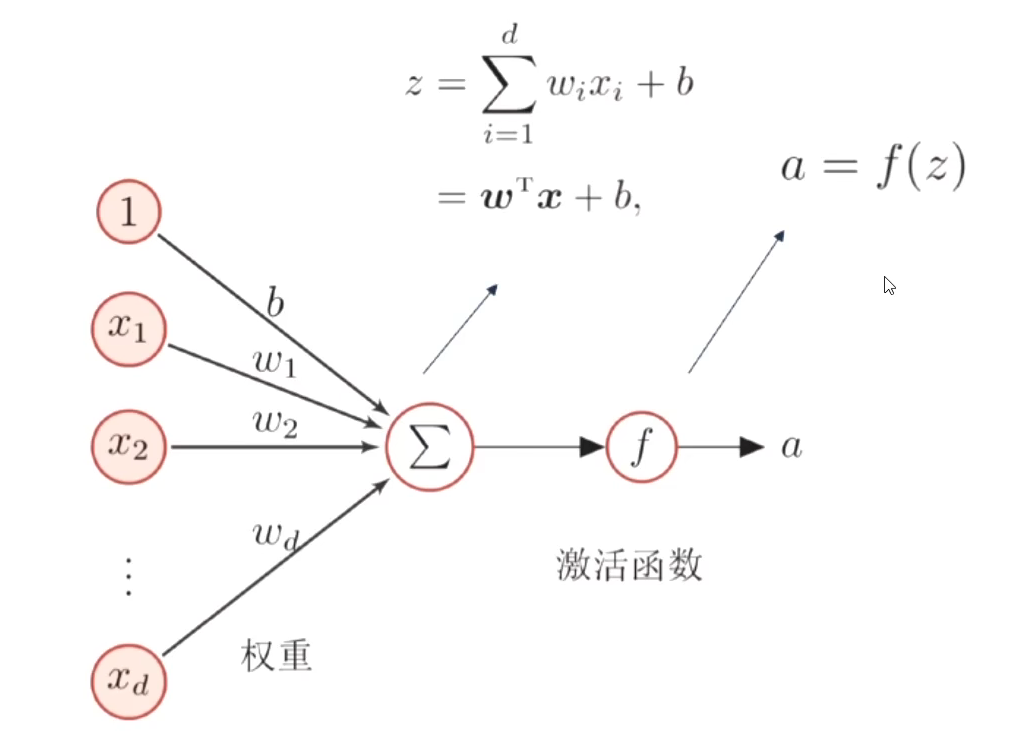
1、神经元与激活函数

• 人工神经元

  

• 常见的激活函数

  sigmoid函数

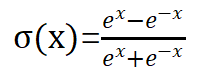
tanh函数（探函数）

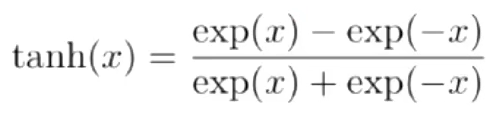
2、前馈神经网络

也成为了全连接神经网络

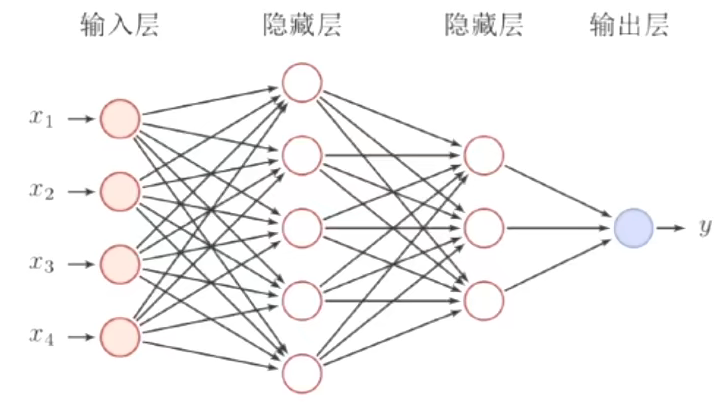
前馈神经网路通过以下公式进行信息传播

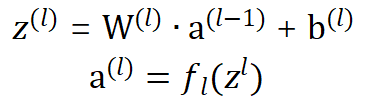
• 变量解释

通用近似定理

参数学习

• 结构化风险函数

  

3、反向传播算法

4、自动梯度计算

• 数值微分
• 符号微分
• 自动微分

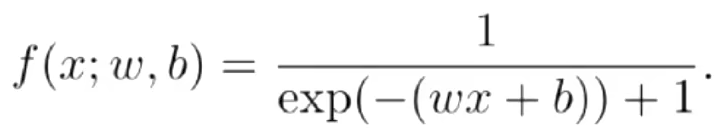
前向模式

x->y,x属于M，y属于N，M小于等于N，则使用前向模式

反向模式

x->y,x属于M，y属于N，M大于等于N，则使用前向模式

5、深度学习的步骤

• 定义网络
• 定义损失函数
• 定义优化器
• 训练
• 测试

6、基于TF2的自动梯度计算实战

已完成

7、Himmeblau函数优化实战

• np.arange(-6,6,0.1)

  0.1代表步长，比如生成的数为-6，-5.9，-5.8

8、前向传播MNIST分类实战

• 第一个激活函数用Relu

• tf.random.truncated_normal([784,256],stddev=0.1)

  创建tensor它是从截断的正态分布中输出随机值，虽然同样是输出正态分布，但是它生成的值是在距离均值两个标准差范围之内的，也就是说，在tf.truncated_normal中如果x的取值在区间（μ-2σ，μ+2σ）之外则重新进行选择。这样保证了生成的值都在均值附近。

  tf.random.truncated_normal( shape, mean=0.0, stddev=1.0, dtype=tf.dtypes.float32, seed=None, name=None )

  • shape 一维整数张量或 Python 数组。输出张量的形状。
  • mean dtype 类型的 0-D 张量或 Python 值。截断正态分布的平均值。
  • stddev dtype 类型的 0-D 张量或 Python 值。截断前正态分布的标准差。
  • dtype 输出的类型。仅限于浮点类型：tf.half、tf.float、tf.double 等。
  • seed 一个 Python 整数。用于为分发创建随机种子。有关详细信息，请参阅tf.random.set_seed。
  • name 操作的名称(可选)。

四、TensorFlow2.0基础

1、变量与张量

2、张量的创建

3、张量的合并与拆分

4、张量的数量统计

5、张量的填充复制

6、tf.gather(),tf.gather_nd()

7、tf.booleanmmask()

8、tf.where()

9、tf. scatter_nd()

10、tf.meshgrid()

11、数据集的加载与预处理

import tensorflow as tf
import numpy as np
tf.__version__

(x_train,y_train),(x_test,y_test)=tf.keras.datasets.mnist.load_data()
x_train.shape

# 将训练集的x与y转换成dataset对象
train_db=tf.data.Dataset.from_tensor_slices((x_train,y_train))
train_db

# 打散数据集
train_db=train_db.shuffle(10000)

# 批训练
# batch_size
# 一份128
train_db=train_db.batch(128)

# 数据预处理
def preprocess(x,y):
       x=tf.cast(x,dtype=tf.float32)/255.
       y=tf.one_hot(y,depth=10)
       return x,y
    
train_db=train_db.map(preprocess)

for x,y in train_db:
       print(x,y)
        
# 一个batch的训练完成--->1个step
# 多个step--->1个epoch
# 多个epoch--->完成一次训练
for epoch in range(20):
       for step,(x,y) in enumerate(train_db):
              # 训练

第五章、Keras高层接口

1、常用模块介绍

1.1 网络容器（Sequential）

对于常见的网络，需要手动调用每一层的类实例完成前向传播运算，当网络层数变得较深时，这一部分代码显得非常臃肿

通过Keras提供的网络容器Sequential将多个网络层封装成一个大网络模型，只需要调用网络模型的实例一次即可完成数据从第一层到最末层的顺序传播运算

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers,Sequential
tf.__version__

network=Sequential([
       # 第一层
       layers.Dense(3),
       layers.ReLU(),
       # 第二层
       layers.Dense(2,activation=layers.ReLU())

])
# 4个样本，3个特征
x=tf.random.normal([4,3])
network(x)

network.summary()
# ------------------------------------------------
Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense (Dense)                multiple                  12        
_________________________________________________________________
re_lu (ReLU)                 multiple                  0         
_________________________________________________________________
dense_1 (Dense)              multiple                  8         
=================================================================
Total params: 20
Trainable params: 20
Non-trainable params: 0
_________________________________________________________________

2、模型的装配、训练与测试

在训练网络时，一般的流程是通过前向计算获得网络的输出值，再通过损失函数计算网络误差，然后通过自动求导工具计算梯度并更新，同时间隔性地测试网络的性能。对于这种常用的训练逻辑，可以直接通过Keras提供的模型装配与训练等高层接口实现

2.1 模型装配

以Sequential容器封装的网络为例，首次创建5层的全连接网络

# 创建5层的全连接网络
model=Sequential([
       layers.Dense(256,activation='relu'),
       layers.Dense(128,activation='relu'),
       layers.Dense(64,activation='relu'),
       layers.Dense(32,activation='relu'),
       layers.Dense(10,activation='softmax')
])
model.build(input_shape=(None,28*28))
model.summary()

创建网络后，正常的流程是循环迭代数据集多个Epoch，每次按批次训练数据、前向计算，然后通过损失函数计算误差值，并反向传播自动计算梯度更新网络参数。这一部分逻辑由于非常通用，在Keras中提供了compile()和fit()函数方便实现上述逻辑。首先通过compile()函数指定网络使用的优化器对象、损失函数类型、评价指标等设定，这一步成为装配。

# 模型装配
# 参数：优化器、损失函数、监控指标
model.compile(
       optimizer=tf.keras.optimizers.SGD(learning_rate=0.001),
       loss=tf.keras.losses.CategoricalCrossentropy(),
       metrics=['accuracy']
)

2.2 模型训练

模型装配完成后，即可通过fit()函数送入待训练的数据集和验证用的数据集，这一步被称为模型训练

# 数据处理函数
def preprocess(x,y):
       x=tf.cast(x,dtype=tf.float32)/255.
       x=tf.reshape(x,[-1,28*28])
       y=tf.one_hot(y,depth=10)
       return x,y

(x_train,y_train),(x_test,y_test)=tf.keras.datasets.mnist.load_data()

# 将训练集的x与y转换成dataset对象
train_db=tf.data.Dataset.from_tensor_slices((x_train,y_train))

# 打散数据集
train_db=train_db.shuffle(10000)

# 批训练
# batch_size
# 一份128
train_db=train_db.batch(128)
 
train_db=train_db.map(preprocess)
train_db

# 模型训练
model.fit(train_db,epochs=5)

fit()函数中，其中train_db为tf.data.Dataset对象，也可以传入Numpy Array类型的数据；epochs参数指定训练迭代的Epoch数量

2.3 模型测试

Mdel基类除了可以便捷地完成网络的装配与训练、验证。还可以非常方便地预测和测试。

通过Model.predict(x)方法即可完成模型的预测

# 周六待完成
#测试数据集预处理
# 将测试集的x与y转换成dataset对象
test_db=tf.data.Dataset.from_tensor_slices((x_test,y_test))

# 打散数据集
test_db=test_db.shuffle(10000)

# 批训练
# batch_size
# 一份128
test_db=test_db.batch(128)
 
test_db=test_db.map(preprocess)

model.predict(test_db)

其中out即为网络的输出。通过上述代码即可使用训练好的模型去预测新样本的标签信息

如果只是简单地测试模型的性能，可以通过Model.evaluate(db)循环测试完db数据集上的所有样本，并打印出性能指标

model.evaluate(test_db)
#结果打印
# 79/79 [==============================] - 1s 11ms/step - loss: 0.4532 - 
# accuracy: 0.8709
# [0.45320446393157865, 0.8709]

3、模型的保存与加载（读取）

一般大规模的网络需要训练数天乃至数周的时长，一旦训练过程被中断或者发生宕（dang）机等意外，之前训练的进度将全部丢失。如果能够间断的保存模型状态到文件系统，即使发生宕机等意外，也可以从最近一次的网络状态文件中恢复，从而避免浪费大量的训练时间。

3.1 张量方式

网络的状态主要体现在网络的结构以及网络层内部张量参数上，因此在拥有网络结构原文件的条件下，直接保存网络张量参数到文件上是最轻量级的一种方式。通过调用Model.save_weights(path)方法即可将当前的网络参数保存到path上

# 当前代码时建立在模型的上一小节的基础之上

!chcp 65001
!echo 中文
!dir # 查看当前目录下的所有文件
# 结果
# 并没有weights.ckpt文件

model.save_weights('weights/weights.ckpt') # 保存模型的所有张量数据

!dir
# 结果
# 出现了weights.ckpt文件

del model # 删除网络对象
model # 再次查看是够存在该网络对象

# 重新创建相同的网络结构
# 创建5层的全连接网络
model=Sequential([
       layers.Dense(256,activation='relu'),
       layers.Dense(128,activation='relu'),
       layers.Dense(64,activation='relu'),
       layers.Dense(32,activation='relu'),
       layers.Dense(10,activation='softmax')
])
model.compile(
       optimizer=tf.keras.optimizers.SGD(learning_rate=0.001),
       loss=tf.keras.losses.CategoricalCrossentropy(),
       metrics=['accuracy']
)

# 从参数文件中读取数据并写入当前网络
model.load_weights('weights/weights.ckpt')
model.evaluate(test_db)

# 79/79 [==============================] - 0s 6ms/step - loss: 0.6889 - accuracy: # 0.8189
# [0.6889308758928806, 0.8189]

这种保存与加载网络的方式最为轻量级，文件中保存的仅仅是参数张量的数值，并没有其他额外的结构参数。但是他需要使用相同的网络结构才能恢复网络状态，因此一般在拥有网络原文件的情况下使用

3.2 网络方式

通过Model.save(path)函数可以将模型的结构以及模型的参数保存到path文件上，在不需要网络原文件的条件下，通过keras.models.load_model(path)即可恢复网络结构和网络参数

# 保存模型结构和模型参数到文件
model.save('model.h5')

del model
model

# 从文件中恢复网络结构和网络参数
model=tf.keras.models.load_model('model.h5')
model.evaluate(test_db)
# 结果
# 79/79 [==============================] - 0s 6ms/step - loss: 0.6883 - accuracy: # 0.8189
# [0.6882536788529987, 0.8189]

3.3 SavedModel方式

TensorFlow之所以能够被业界青睐，除了优秀的神经网络层API支持外，还得益于它强大的生态系统，包括移动端和网页端等的支持。当需要将模型部署到其他平台时，采用TensorFlow提出的SavedModel方式更具有平台无关性

通过tf.keras.models.save_model(model,'saved_model')即可将模型以SavedModel方式保存到path目录中

用户无需关心文件的保存格式，只需要通过model=tf.keras.models.load_model('saved_model')函数即可恢复模型对象，再恢复模型实例后，就即可以进行测试集测试准确率

# SavedModel方式
# 保存模型结构与模型参数到文件中
tf.keras.models.save_model(model,'saved_model')

del model

# 从文件中恢复网络结构与网络参数
model=tf.keras.models.load_model('saved_model')

model
# 返回的是Sequential对象
# <tensorflow.python.keras.saving.saved_model.load.Sequential at 0x1f60b1a1908>

model.evaluate(test_db)
# 测试结果依旧合适
# 79/79 [==============================] - 1s 8ms/step - loss: 0.6886 - accuracy: # 0.8206
# [0.6886198052877113, 0.8206]

4、自定义网络层和模型

4.1 自定义网络层

自定义网络层需要继承tf.keras.layers.Layer类，并重写init、build和call三个方法，如下所示：

• init(前后两条下划线)，你可以在其中执行所有与输入无关的初始化
• build，你可以在其中了解输入张量的形状，并可以执行其余的初始化
• call，在那里进行正向计算

import tensorflow as tf
from tensorflow.keras import layers
tf.__version__

# 自定义全连接层
class MyDense(layers.Layer):

       def __init__(self,units):
              super().__init__()
              self.units=units

       def build(self,input_shape):
              # input_shape=[60000,784]

              # w的形状
              # 第一个维度，输入的x的特征数
              # 第二个维度，神经元的个数
              self.w=self.add_variable(
                     name='w',
                     shape=[input_shape[-1],self.units],
                     initializer=tf.initializers.RandomNormal()
              )
              self.b=self.add_variable(
                     name='b',
                     shape=[self.units],
                     initializer=tf.initializers.Zeros()
              )

       def call(self,inputs):
              # w*x+b
              # w的形状： [input_shape[-1],units]
              # x [60000,784]
              return inputs @ self.w+self.b
            
L1=MyDense(10) # 10是神经元的个数

x=tf.zeros([20,15])
L1(x) # 调用call方法和build方法，x的值也同时传给了input_shape
# 输出结果，输出数据形状为(20,10)=(20,15)@(15,10)
<tf.Tensor: shape=(20, 10), dtype=float32, numpy=
array([[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]], dtype=float32)>

# 查看类的全部参数列表
L1.trainable_variables 

4.2 自定义网络（模型）

创建自定义的网络类时，需要继承自keras.Model基类，这样建立的自定义类才能够方便的利用Model基类提供的参数管理等功能，同时也能与其他的标准网络层类交互使用

下面基于自定义的网络层来实现mnist手写数字模型的创建

# 自定义模型类
class MyModel(Model):

       def __init__(self):
              super().__init__()

              # 完成网络内需要的网络层的创建工作
              # 前三层使用relu激活函数，最后一层使用softmax函数
              self.fc1=MyDense_relu(512)
              self.fc2=MyDense_relu(256)
              self.fc3=MyDense_relu(128)
              self.fc4=MyDense_softmax(10)

       def call(self,inputs):
              # 自定义前向运算逻辑
              fc1_out=self.fc1(inputs)
              print(fc1_out)
              fc2_out=self.fc2(fc1_out)
              print(fc2_out)
              fc3_out=self.fc3(fc2_out)
              print(fc3_out)
              fc4_out=self.fc4(fc3_out)
              print(fc4_out)
              return fc4_out
# 模型装配
myModel=MyModel()
myModel.build(input_shape=(None,784))
myModel.summary()

# 优化器
myModel.compile(
       optimizer=tf.keras.optimizers.SGD(),
       loss=tf.keras.losses.CategoricalCrossentropy(),
       metrics=['accuracy']
)

# 数据处理函数
def preprocess(x,y):
       x=tf.cast(x,dtype=tf.float32)/255.
       x=tf.reshape(x,[-1,28*28])
       y=tf.one_hot(y,depth=10)
       return x,y

(x_train,y_train),(x_test,y_test)=tf.keras.datasets.mnist.load_data()

# 将训练集的x与y转换成dataset对象
train_db=tf.data.Dataset.from_tensor_slices((x_train,y_train))

# 打散数据集
train_db=train_db.shuffle(10000)

# 批训练
# batch_size
# 一份128
train_db=train_db.batch(128)

train_db=train_db.map(preprocess)

# 将测试集的x与y转换成dataset对象
test_db=tf.data.Dataset.from_tensor_slices((x_test,y_test))

# 打散数据集
test_db=test_db.shuffle(10000)

# 批训练
# batch_size
# 一份128
test_db=test_db.batch(128)
 
test_db=test_db.map(preprocess)

# 模型训练
myModel.fit(train_db,epochs=10)

# 模型测试
myModel.evaluate(test_db)

5、测量工具与可视化

六、卷积神经网络

1、全连接前馈神经网络存在的问题

• 权重矩阵参数特别多
• 局部不变性特征

2、什么是卷积

• 一维卷积

• 二维卷积

• 互相关

  除非特别说明，卷积一般指互相关

  互相关和卷积的区别在于不做翻转，对参数的学习没有影响

3、步长和填充

4、通道与卷积核

• 单通道输入-单卷积核

  不需要翻转

  灰色图片

  直接点积求和

• 多通道输入-单卷积核

  彩色图片

• 多通道输入-多卷积核

5、卷积运算

5.1 自定义权值

自定义输入和卷积核

• 通过tf.nn.conv2d函数可以方便地实现2D卷积运算

• 卷积层实现代码

  padding='same'操作：在已知步长情况下向右滑动，不够时感受野通过补0计算

  padding='valid':不够时直接抛弃

5.2 卷积层类

• 通过卷积层类layers.Conv2D可以不需要手动定义卷积核W和偏置b张量，直接调用类示例即可完成卷积层的前向计算，实现更加高层和快捷

6、池化层（汇聚层、下采样层）

在卷积层中，可以通过调节步长参数s实现特征图的高、宽成倍缩小，从而降低了网络的参数量。实际上，除了通过设置步长，还有一种专门的网络层可以实现尺寸缩减功能，就是池化层

在卷积层提取到的特征数据不具备空间不变性（尺度与迁移不变性特征），只有通过了池化层之后才会具备空间不变性特征

防止过拟合

过大的采样区会造成信息丢失

7、卷积网络结构

• 典型卷积神经网络分类结构

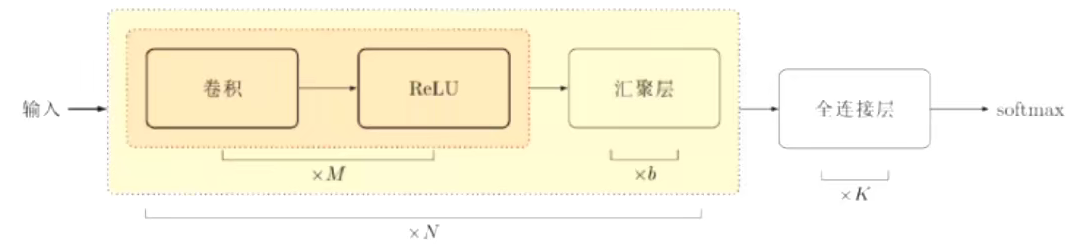
8、表示学习

思想：网络层数越深，模型的表达能力越强，也就越有可能取得更好的性能

9、梯度传播

卷积层通过移动感受野的方式实现离散卷积操作，那么它的梯度传播是怎么进行的？

讨论下面这种情况下的梯度更新方式

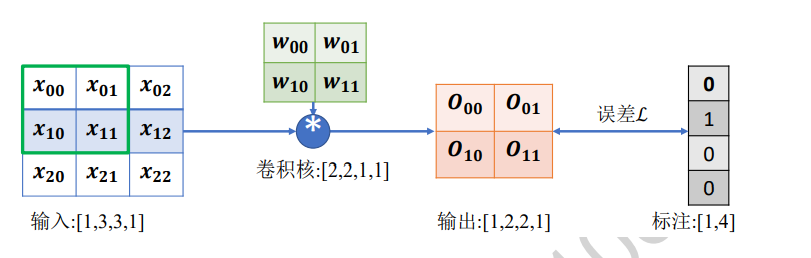
• 首先推导输出张量O的表达形式

  

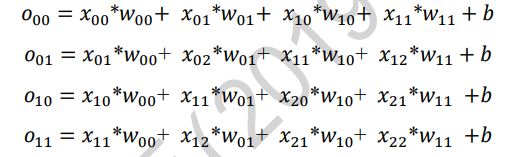
• 以W00的梯度计算为例，通过链式法则分解：

  

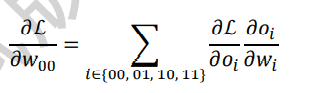
• 其中L对o的导数可直接由误差函数推导出来，直接考虑o对w的导数

  

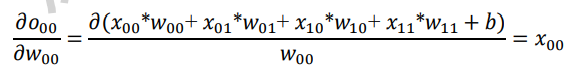
• 同样的方法，可以推导出：

  

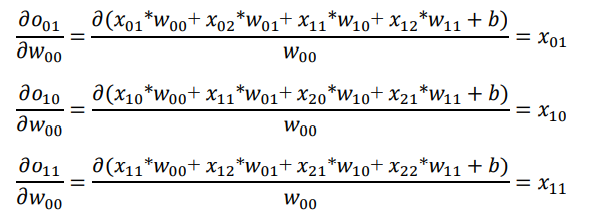
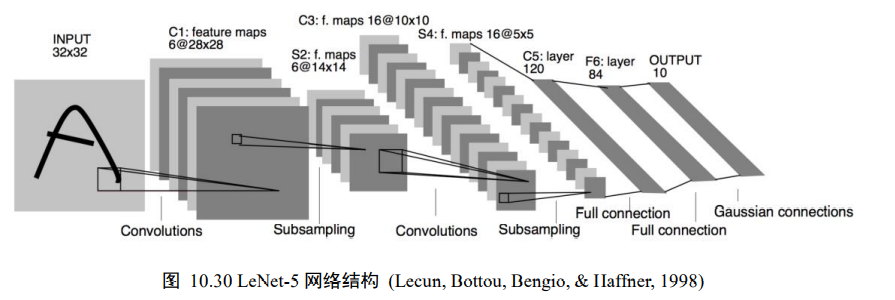
10、LeNet-5实战

LeNet-5的网络结构，他接受32x32大小的数字、字符图片，经过第一个卷积层得到[b,28,28,6]形状的张量，经过一个向下采样层，张量尺寸大小缩小到[b,14,214,6]，经过第二个卷积层，得到[b,10,10,16]形状的张量，同样经过下采样层，张量尺寸缩小到[b,5,5,16]，在进入全连接层前，先将张量打成[b,400]的张量，送入输出节点数分别为120、84的2个全连接层，得到[b，84]的张量，最后通过Gaussian connections层

• 现代深度学习框架上实现LeNet-5网络模型

  网络结构如图

  

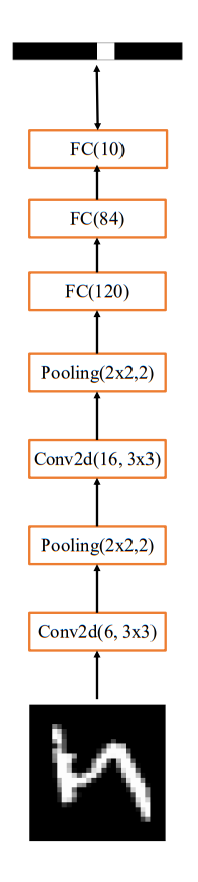
• 通过Sequential容器创建LeNet-5，代码如下

  network = Sequential([ #网络容器
      layers.Conv2D(6,kernel_size=3,strides=1),#第一个卷积层，6个3x3卷积核
      layers.MaxPooling2D(pool_size=2,strides=2),# 高宽各减半的池化层
      layers.ReLU (),#激活函数
      layers.Conv2D(16, kernel_size=3,strides=1),#第二个卷积层，16个3x3卷积核
      layers.MaxPooling2D(pool_size=2,strides=2),# 高宽各减半的池化层
      layers.ReLU(),# 激活函数
      layers.Flatten(),#打平层，方便全连接层处理
      layers.Dense (120,activation='relu'),#全连接层，120个节点
      layers.Dense (84,activation='relu ' ),#全连接层，84节点
      layers.Dense ( 10)#全连接层，10个节点
  # build一次网络模型，给输入x的形状，其中4为随意给的batchsz
  network.build(input_shape= (4,28,28,1))
  #统计网络信息
  network.summary()
  

  通过summary函数可以统计出每层的参数量，打印出网络结构信息和每层参数量详情

11、AlexNet

第一个现代深度卷积网络模型，创新点在于：

• 使用GPU进行并行训练

• 采用Relu作为非线性激活函数

• 使用Dropout放置过拟合

  删除隐藏层中一般的神经元，更新未隐藏的神经元的参数，再隐藏。。。

• 使用数据增强技术

• 层叠池化

  池化层是可以重叠的

• 局部响应归一性

模型结构

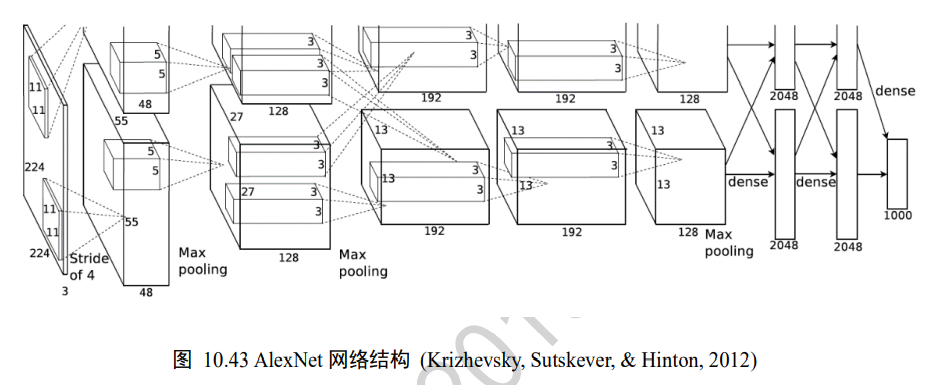
第一个卷积层C1

• 输入C1（227,227,3）的图片数据

• 通过一次卷积得到（55,55,96）的张量，55=（227-11+0）/4+1,96=48+48，一个GPU的通道数是48，将两个GPU的通道数叠加

• 经过一次Relu激活函数

• 经过一次池化，张量尺寸缩小到（27,27,96），27=（55-3+0）/2+1

• 在经过一次局部响应归一化

• 完成第一个卷积层操作

12、BN层（批量标准化）

Batch Normalization

卷积神经网络的加深使得网络训练变得非常不稳定，甚至会出现网络长时间不更新甚至不收敛的情况，同时网络对超参数比较敏感，超参数的微量扰动也会导致网络的训练轨迹完全改变

优点

• 网络的超参数设定更加自由
• 网络收敛速度更快，性能更高

12.1 目的

网络层输入x分布相近，并且分布在较小范围内时（如0）附近，更有利于函数的优化。name如何保证输入x的分布相近？数据标准化可以实现此目的

12.2 步骤

• 通过数据标准化操作可以将数据x映射到x冒

  

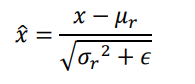
μr和δr^2来自统计的所有数据的均值和方差，ε是防止出现除0错误而设置的较小数字

• 考虑Batch内部的均值μb和方差δb^{2可以视为近似于μr和δr}2

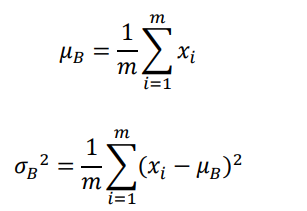
其中m为Batch样本数

• 在训练阶段，通过标准化输入，并记录每个Batch的μb、δb^{2估计除所有训练数据的μr、δr}2

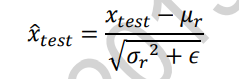
• 在测试阶段，根据记录的每个Batch的μb、δb^{2估计出所有训练数据的μr、δr}2，按照下面的公式将每层的数据标准化

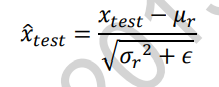
μr、δr^{2、μb、δb}2不需要参与到梯度更新

• 引入scale and shift技巧，将x冒变量再次映射变换

  

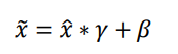
其中，γ参数实现对x冒的缩放，β实现对x冒的平移，γ、β参数均由反向传播算法自动进行参数优化

12.3 实战

把reshape操作注释掉

import tensorflow as tf 
from tensorflow import keras
tf.__version__

#[b,h,w,c]
x=tf.random.normal([100,32,32,3])

# 拉平
# x=tf.reshape(x,[-1,3])
x

tf.reduce_mean(x,axis=0)

model=keras.Sequential([
       keras.layers.Conv2D(6,3),
       keras.layers.BatchNormalization(),
       keras.layers.ReLU(),
       keras.layers.MaxPool2D()
])

out=model(x)
model.variables

13、VGG网络模型

在进行VGG网络模型构建实战中可能会出现loss值没有按理想的预期值逐渐递减，而是呈现不规则的变化，如下图

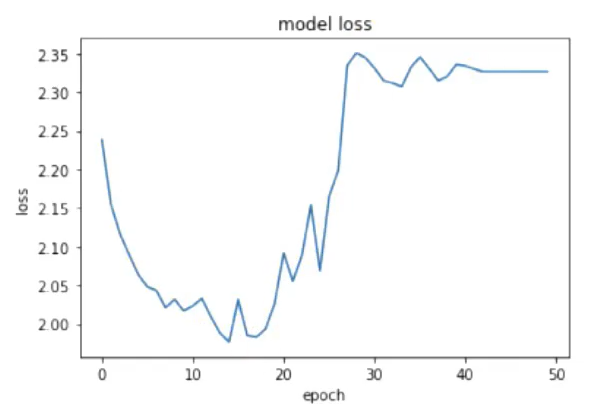
此时可采用以下方式进行模型优化

• 调低学习率（或者按照迭代次数衰减）
• 调整参数的初始化方法
• 调整输入数据的初始化方法
• 修改loss函数
• 增加正则化
• 使用BN/GN层（中间层数据的标准化）
• 使用dropout
• 其他......

14、GoogLeNet网络模型

GoogLeNet网络采用模块化设计的思想，通过大量堆叠Inception模块，形成了复杂的网络结构

Inception模块如下图

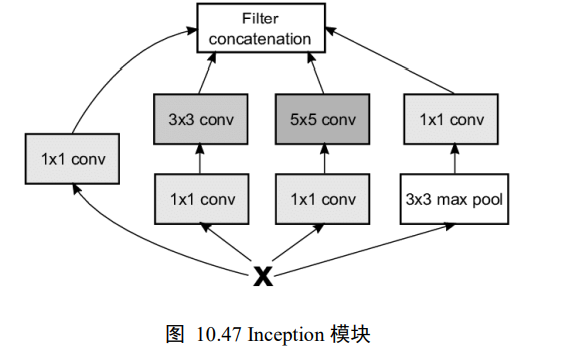
• 1x1卷积层
• 1x1卷积层，再通过一个3x3卷积层
• 1x1卷积层，再通过一个5x5卷积层
• 3x3最大池化层，再通过一个1x1卷积层

15、深度残差网络（ResNet）

ResNet通过在卷积层的输入和输出之间添加Skip Connection实现层数回退机制

输入x通过两个卷积层，得到特征变换后的输出F(x)，与输入x进行对应元素额的相加运算，得到最终输出H(x):

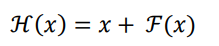
H(x)称为残差模块（Residual Block,ResBlock）。由于被Skip Connection保卫的卷积神经网络需要学习映射F(x)=H(x)-x,故称为残差网络。

为了能够满足输入x与卷积层的输出F(x)相加运算，需要输入x的shape与F(x)的shape完全一致

16、卷积层变种

16.1 空洞卷积

通过给卷积核插入“空洞”来变相的增加其大小

16.2 转置卷积

转置卷积通过在输入之间填充大量的padding来实现输出高、宽大于输入高、宽的效果，从而实现向上采样的目的。

17、CNN结构演化历史

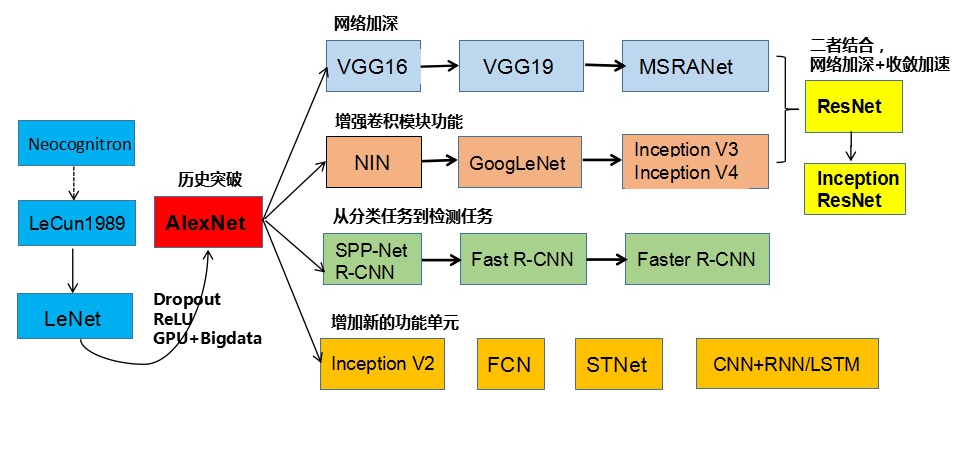
第七章、循环神经网络

主要用来处理具有时间局部相关性的数据

1、序列表示方法

1.1 语义相关性

在自然语言处理领域，有专门的一个研究方向在探索如何学习到单词的表示向量（Word Vector），使得语义层面的相关性能够很好的通过Word Vector 体现出来。一个衡量词向量之间相关度的方法就是余弦相似度（Cosine similarity）

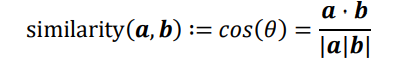
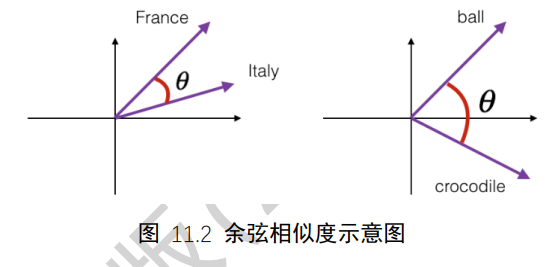
其中a，b代表了两个词向量。下图演示了单词France和Italy的相似度，以及单词ball（球）和crocodile（鳄鱼）的相似度，θ为两个词向量之间的夹角。可以看到cos(θ)较好的反映了语义相关性

1.2 Embedding层

Embedding是一个将离散变量转为连续变量表示的一个方式

Embedding层负责把单词编码为某个词向量v，它接受的是采用数字编码的单词编号i；如2表示I，3表示me等，单词总数量记为N，输出长度为n的向量v

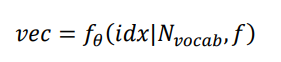
Embedding层实现起来非常简单，构建一个shape为[N,n]的查询表对象table，对于任何的单词编号i，只需要查询到对应位置上的向量并返回即可。

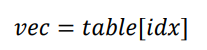
查询表对象如下：

2、循环神经网络

2.1 全连接层可行吗？

• 参数量太大
• 每个句子的长度不一致
• 每个全连接层子网络Wi和bi只能感受当前词向量的输入，并不能感知之前和之后的语境信息，导致整体语义的缺失

2.2 全局语义

现在考虑如何处理序列信号，以文本序列为例，考虑一个句子：I hate this the boring movie

• 通过Embedding层可以将它转换为shape为[b,s,n]的张量，b为句子数量，s为句子长度，n为词向量长度。上述句子可以表示为shape为[1,5,10]的张量

全局语义：让网络能够按序提取词向量的语义信息，并累积成整个句子的全局语义信息

• 使用Memory机制实现一个状态张量h，如下图，除了原来的Wxh参数共享外，这里额外增加了一个Whh参数，

  

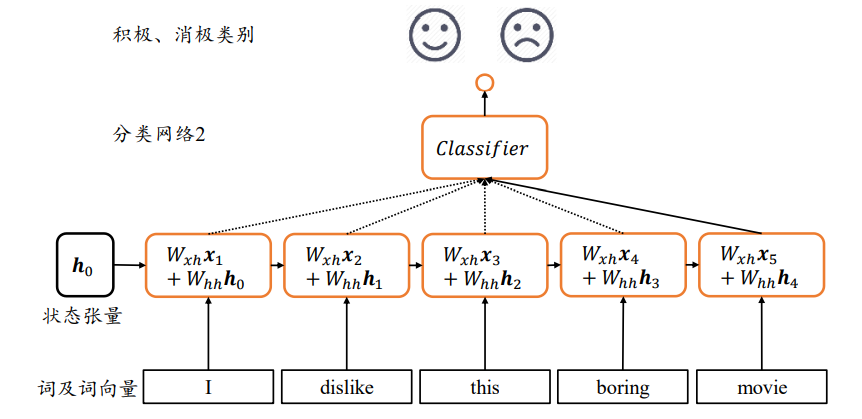
每个时间戳t上状态张量h的刷新机制为：

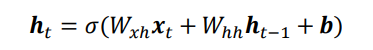
• 其中状态张量h0为初始的内存状态，可以初始化为全0，经过s个词向量的输入后得到网络最终的状态张量hs，hs较好的代表了句子的全局语义信息，基于hs通过某个全连接层分类器即可完成情感分类任务

2.3 循环神经网络原理

原理

• 在每个时间戳t，网络层接收当前时间戳的输入xt和上衣和时间戳的网络状态向量h(t-1)，经过

  

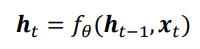
变换后得到当前时间戳的新状态向量ht，并写入内存状态中，其中fθ代表了网络的运算逻辑，θ为网络参数集。在每个时间戳上，网络层均由输出产生Ot，Ot=GΦ(Ht),即将网络的状态向量变换后输出。

概念

• 上述网络结构在时间戳上折叠，如下图，网络循环接受序列的每个特征向量xt，并刷新内部状态向量ht，同时形成输出ot。对于这种结构，我们把他成为循环神经网络（Recurrent Neural Network,RNN ）

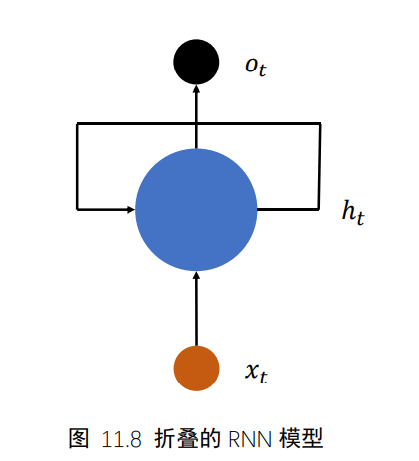
• 更特别的，如果使用张量Wxh，Whh和偏置b来参数化fθ网络，并按照

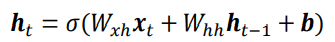
方式更新内存状态，把这种网络成为基本的循环神经网络。

• 如无特别说明，一般说的循环神经网络即指基本的循环神经网络

循环神经网络结构

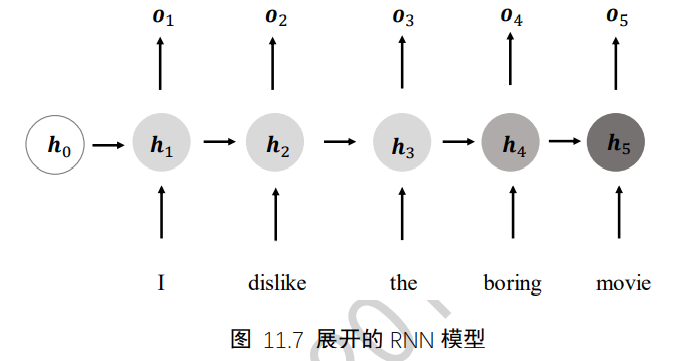
3、梯度传播

在推导梯度的过程中，发现包含了Whh的连乘操作，这是导致循环神经网络训练困难的根本原因

4、RNN层使用方法

SimpleRNN与SimpleRNNCell的区别在于，带Cell的层仅仅只是完成了一个时间戳的前向运算，不带Cell的层一般是基于Cell层实现的，他在内部已经完成了多个时间戳的循环运算，因此使用起来更加方便快捷。

4.1 SimpleRNNCell（实战）

# 初始化状态向量，用列表包裹，统一格式
h0=[tf.zeros([4,64])]
x=tf.random.normal([4,80,100]) # 生成输入张量，4个80单词的句子
xt=x[:,0,:] # 所有句子的第一个单词
# 构建输入特征n=100，序列长度s=80，状态长度=64的Cell
cell=layers.SimpleRNNCell(64)
out,h1=cell(xt,h0) # 前向计算
print(out.shape,h1[0].shape)
# Out[4]:(4,64),(4,64)

# 对于长度为s的训练来说，需要循环通过Cell类s次才算完成一次网络层的前向运算
h=h0
# 在序列长度的维度解开输入，得到xt:[b,n]
for xt in tf.unstack(x,axis=1):
    out,h=cell(xt,h)
# 最终输出可以聚合每个时间戳上的输出，也可以只取最后时间戳的输出
out=out

# 最后一个时间戳的输出变量out将作为网络的最终输出。实际上，也可以将每个时间戳上的输出保存，然后求和或者均值，将其作为网络的最终输出

4.1 SimpleRNN层

• 完成单层循环神经网络的前向运算：

layer = layers.SimpleRNN(64) # 创建状态向量长度为64的SimpleRNN层
x = tf.random.normal([4, 80, 100])
out = layer(x) # 和普通卷积网络一样，一行代码即可获得输出
out.shape

# Out[6]: TensorShape([4, 64] 
# 默认返回最后一个时间戳上的输出

• 如果希望返回所有时间戳上的列表，可以设置return_sequences=True参数

# 创建RNN层时，设置返回所有时间戳上的输出
layer = layers.SimpleRNN(64,return_sequences=True) 
out = layer(x) # 前向计算
out # 输出，自动进行了concat操作
#    Out[7]:
#    <tf.Tensor: id=12654, shape=(4, 80, 64), dtype=float32, numpy=
#    array([[[ 0.31804922, 0.7904409 , 0.13204293, ..., 0.02601025,
#    -0.7833339 , 0.65577114],…>

返回的输出张量shape为[4,80,64]，中间维度的80即为时间戳维度

• 对于多层循环神经网络，可以通过堆叠多个SimpleRNN实现，如两层的网络，用法和普通的网络类似

model=keras.Sequences([ # 构建2层的RNN网络
    # 除最末层外，都需要返回所有时间戳的输出，用作下一层的输入
    layers.SimpleRNN(64,return_requences=True)
    layers.SimpleRNN(64)
])
out = net(x) # 	前向计算

5、梯度弥散和梯度爆炸

5.1 概念

循环神经网络的训练并不稳定，网络的深度也不能任意地加深。那么为什么会出现训练困难的问题？简单回顾梯度推导中的关键表达式：

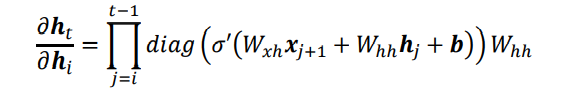
也就是说，从时间戳i到时间戳t的梯度ht对hi的偏导（之后记作grad）包含了Whh的连乘运算。当Whh的最大特征值小于1时，多次连乘运算会使得grad的元素值解接近0；当grad的值大于1时，多次连乘运算会使得grad的元素值爆炸式增长

• 把梯度值接近0的现象称为梯度弥散
• 把梯度值远大于1的现象称为梯度爆炸

5.2 梯度裁剪

梯度爆炸可以通过梯度裁剪（Gradient Clipping）的方式在一定程度上得到解决。梯度裁剪与张量限幅非常类似，也是通过将梯度张量的数值或者范数限制在某个较小的区间内，从而将远大于1的梯度值减少，避免出现梯度爆炸

5.3 梯度弥散

对于梯度弥散现象，可以通过增大学习率，减少网络深度、添加Skip Connection(短接)等一系列的措施抑制。

6、RNN短时记忆

循环神经网络在处理较长的句子时，往往只能够理解有限长度内的信息，而对于较长范围内的有用信息往往不能够很好地利用起来。把这种现象称为短时记忆

7、LSTM原理

7.1 LSTM结构

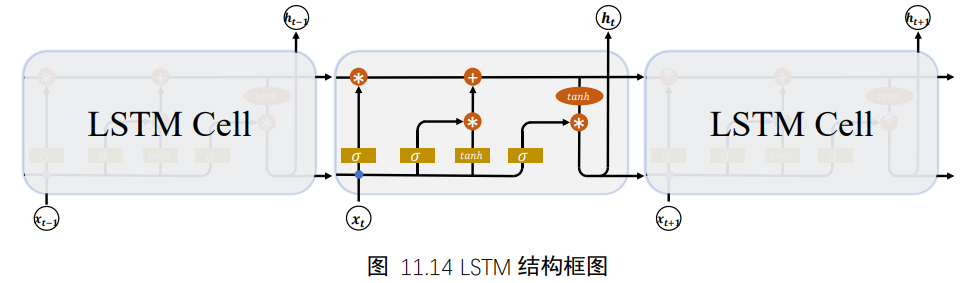
相对于基础的RNN网络只有一个状态向量h，LSTM新增了一个状态向量Ct，同时引入了门控机制，通过门控单元来控制信息的遗忘和刷新

在LSTM中，有两个状态向量c和h，其中c作为LSTM的内部状态向量，可以理解为LSTM的内存状态向量Memory，而h表示LSTM的输出向量。相对于基础的RNN来说，LSTM把内部Memory和输出分开为两个变量，同时利用三个门控：输入门（Input Gate）、遗忘门（Forget Gate）和输出门（Output Gate）来控制内部信息的流动

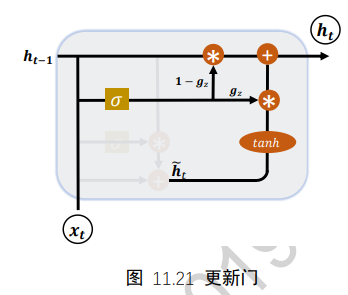
7.2 门控机制

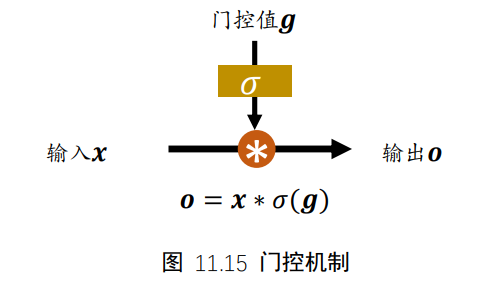
通过σ(g)激活函数将门控压缩到[0,1]区间，当σ(g)=0时，门控全部关闭，输出o=0；当σ(g)=1时，门控全部打开，输出o=x。通过门控机制可以较好地控制数据的流量程度。

7.3 遗忘门

遗忘门作用于LSTM状态向量c上面，用于控制上一个时间戳的记忆Ct-1对当前时间戳的影响。遗忘门的控制变量gf由下图公式产生，其中Wf和bf为遗忘门的参数张量，可有反向传播算法自动优化。σ为激活函数，一般使用Sigmoid函数。当门控gf=1时。遗忘门全部打开，LSTM接受上一个状态Ct-1的所有信息；当门控gf=0时，遗忘门关闭，LSTM直接忽略Ct-1，输出位0的向量。

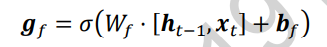
遗忘门的结构如下：

经过遗忘门后，LSTM的状态向量变为gf*Ct-1

7.4 输入门

输入门用于控制LSTM对输入的接收程度。首先通过对当前时间戳的输入xt和上一个时间戳的输出ht-1做非线性变换得到新的输入变量ct冒

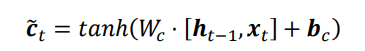
其中Wc和bc为输入门的参数，需要通过反向传播算法自动优化，tanh为激活函数，用于将输入标准化到[-1,1]区间。ct冒并不会全部刷新进入LSTM的Memory，而是通过输入们控制接受输入的量。输入门的控制变量同样来自于输入xt和输出ht-1

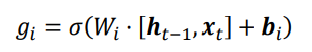
其中Wi和bi为输入门的参数，需要通过反向传播算法自动优化，σ为激活函数，一般使用Sigmoid函数。输入门控制变量gi决定了LSTM对当前时间戳的新输入ct冒的接受程度：当gi=0时，LSTM不接受任何的新输入ct冒；当gi=1时，LSTM全部接受新输入ct冒。如下图：

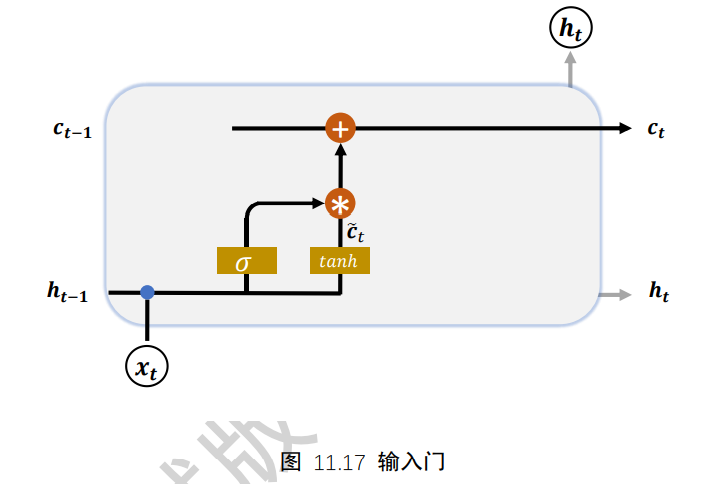
经过输入门后，待写入Memory的向量为gi*ct冒

7.5 刷新Memory

在遗忘门和输入门的控制下，LSTM有选择的读取了上一个时间戳的记忆ct-1和当前时间戳的新输入ct冒，状态向量ct的刷新方式如下公式，得到的新状态向量ct即为当前时间戳的状态向量

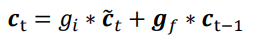
7.6 输出门

LSTM的内部状态向量ct并不会直接用于输出，这一点和基础的RNN不一样。基础的RNN网络的状态向量h既用于记忆，又用于输出，所以基础的RNN可以理解为状态向量c和输出向量h是用一向量。在LSTM内部，状态向量并不会全部输出，而是在输出门的作用下有选择的输出。输出门的门控变量go为：

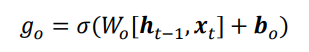
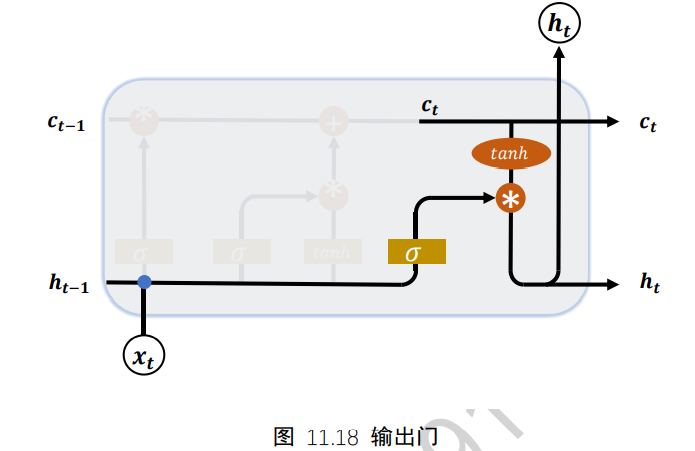
其中Wo和bo为输出门的参数，同样需要通过反向传播算法自动优化，σ为激活函数，一般使用Sigmoid函数。当输出门go=0时，输出关闭，LSTM的内部记忆完全被隔断，无法用作输出，此时输出为0的向量；当输出门go=1时，输出完全打开，LSTM的状态向量ct全部用于输出。LSTM的输出由下面的公式产生，即内存向量ct，经过tanh激活函数与输入门作用，得到LSTM的输出。由于go∈[0,1],tanh∈[-1,1],因此LSTM的输出ht∈[-1,1]

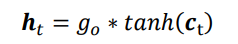
输出门的结构如下：

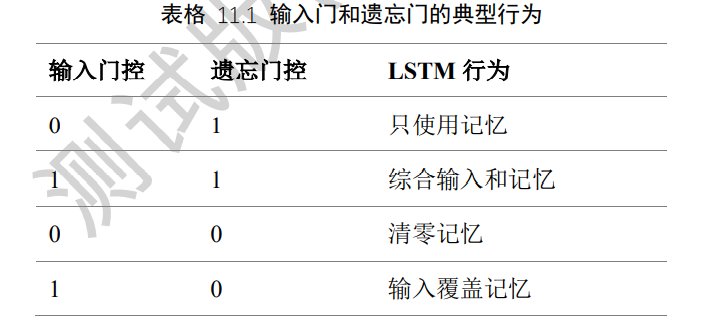
7.7 典型的门控行为

7.8 实战

import tensorflow as tf
import matplotlib.pyplot as plt
from tensorflow import keras
tf.__version__

(x_train,y_train),(x_test,y_test)=tf.keras.datasets.imdb.load_data()

x_train=keras.preprocessing.sequence.pad_sequences(x_train,maxlen=250)
x_test=keras.preprocessing.sequence.pad_sequences(x_test,maxlen=250)

train_db=tf.data.Dataset.from_tensor_slices((x_train,y_train))
test_db=tf.data.Dataset.from_tensor_slices((x_test,y_test))

train_db=train_db.shuffle(10000).batch(128,drop_remainder=True) 
test_db=train_db.shuffle(10000).batch(128,drop_remainder=True) 

class myLSTMCell(keras.Model):
    def __init__(self):
        super().__init__()
        self.state_0=[tf.zeros([128,64]),tf.zeros([128,64])]
        self.state_1=[tf.zeros([128,32]),tf.zeros([128,32])]
        self.embedding=keras.layers.Embedding(input_dim=100000,output_dim=100)
        self.lstm_cell_0=keras.layers.LSTMCell(64)
        self.lstm_cell_1=keras.layers.Cell(32)
        self.fc=keras.layers.Dense(1)

    def call(self,inputs):
        x=self.embedding(inputs)
        state_0=self.state_0
        state_1=self.state_1

        for x in tf.unstack(x,axis=1):
            out_0,state_0=self.lstm_cell_0(x,state_0)
            out_1,state_1=self.lstm_cell_1(out_0,state_1)
        x=self.fc(out_1)
        x=tf.sigmoid(x)
        return x 
    
model=myLSTMCell()
model.compile(
    optimizer=keras.optimizers.Adam(0.001),
    loss=keras.losses.BinaryCrossentropy(from_logits=True),
    metrics=['accuracy']
)

history=model.fit(train_db,epochs=10)

plt.plot(history.history['loss'])

8、GRU简介

8.1 概念

LSTM结构相对比较复杂，计算代价较高、模型参数量较大。

研究发现，遗忘门是LSTM中最重要的门控。

门控循环网络（GRU）是应用最广泛的RNN变种之一。GRU把内部状态向量和输出向量合并，统一为状态向量h。门控数量也减少到2个：复位门和更新门

8.2 复位门

• 复位门用于控制上一个时间戳的状态ht-1进入GRU的量。门控向量gr由当前时间戳输入xt和上一个时间戳ht-1变换得到：关系如下：

  

其中Wr和br为复位门的参数，由反向传播算法自动优化，σ为激活函数，一般使用Sigmoid函数。门控向量gr只控制状态ht-1，而不会控制输入xt：

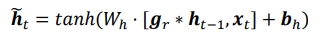
当gr=0时，新输入ht冒全部来自于输入xt，不接受ht-1，此时相当于复位ht-1。当gr=1时，ht-1和输入xt共同产生新输入ht冒。如下图

8.3 更新门

• 更新门用于控制上一时间戳状态ht-1和新输入ht冒对新状态向量ht的影响程度。更新门控向量gz由下图公式得到

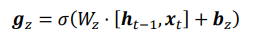
其中Wz和bz为更新门的参数，由反向传播算法自动优化，σ为激活函数，一般使用Sigmoid函数。gz用于控制新输入ht冒信号，1-gz用于控制状态ht-1信号：

可以看到，ht冒和ht-1的更新量处于相互竞争、此消彼长的状态。当更新门gz=0时，ht全部来自上一时间戳状态ht-1；当更新门状态gz=1时，ht全部来自新输入ht冒

8.4 实战

import tensorflow as tf
import matplotlib.pyplot as plt
from tensorflow import keras
tf.__version__

(x_train,y_train),(x_test,y_test)=tf.keras.datasets.imdb.load_data()

x_train=keras.preprocessing.sequence.pad_sequences(x_train,maxlen=250)
x_test=keras.preprocessing.sequence.pad_sequences(x_test,maxlen=250)

train_db=tf.data.Dataset.from_tensor_slices((x_train,y_train))
test_db=tf.data.Dataset.from_tensor_slices((x_test,y_test))

train_db=train_db.shuffle(10000).batch(128,drop_remainder=True) 
test_db=train_db.shuffle(10000).batch(128,drop_remainder=True) 

class myGRUCell(keras.Model):
    def __init__(self):
        super().__init__()
        self.state_0=[tf.zeros([128,64]),tf.zeros([128,64])]
        self.state_1=[tf.zeros([128,32]),tf.zeros([128,32])]
        self.embedding=keras.layers.Embedding(input_dim=100000,output_dim=100)
        self.gru_cell_0=keras.layers.GRUCell(64)
        self.gru_cell_1=keras.layers.GRUCell(32)
        self.fc=keras.layers.Dense(1)

    def call(self,inputs):
        x=self.embedding(inputs)
        state_0=self.state_0
        state_1=self.state_1

        for x in tf.unstack(x,axis=1):
            out_0,state_0=self.gru_cell_0(x,state_0)
            out_1,state_1=self.gru_cell_1(out_0,state_1)
        x=self.fc(out_1)
        x=tf.sigmoid(x)
        return x 
    
model=myGRUCell()
model.compile(
    optimizer=keras.optimizers.Adam(0.001),
    loss=keras.losses.BinaryCrossentropy(from_logits=True),
    metrics=['accuracy']
)

history=model.fit(train_db,epochs=10)

plt.plot(history.history['loss'])

9、循环神经网络的应用

• 一对一：最为简单的反向传播算法
• 一对多：可用于图像捕捉，将图像转换为文字
• 多对一：常用于情感分析，将一句话中轨为具体的情感类别
• 多对多：常用语输入输出序列长度不确定时，例如机器翻译，实质上是两个神经网络的叠加
• 不确定长度的多对多：常用于语音识别中，输入与输出序列等长

第八章 自编码器

1、 无监督学习

无监督学习是指从无标签的数据中学习出一些有用的模式

• 监督学习

  建立映射关系f:x->y

• 无监督学习

  • 建立映射关系f:x->y

    不借助于任何人工给出标签或者反馈等指导信息

  • 密度估计p(x)

典型的无监督学习问题

• 无监督学习特征
• 密度估计
• 聚类

2 、无监督特征学习方法

2.1 PCA（Principle component analysis）：主成分分析

PCA是一种常用的数据分析方法。PCA通过线性变换将原始数据变换为一组各维度线性无关的表示，可用于数据的主要特征分量，常用于高维数据的降维

如果我们有一组N维向量，现在要将其降到K维（K小于N），那么我们应该如何选择K个基才能最大程度保留原有的信息？如果我们必须使用一维来表示这些数据，又希望尽量保留原始的信息，应该如何选择？

这个问题实际上是要在二维平面中选择一个方向，将所有数据都投影到这个方向所在直线上，用投影值表示原始数据。那么如何选择这个方向（或者说基）才能保留最多的原始信息呢？一种直观的看法就是：希望投影后的投影值尽可能分散

• 方差

我们希望投影后的投影值尽可能分散，而这种分散程度。可以用数学上的方差来表示。

于是上面的问题被形式化表示为：寻找一个基，是得所有数据变换为这个基上的坐标表示后，方差值最大

• 协方差

对于二维降成一维的问题来说，找到那个使得方差最大的方向就可以了。不过对于高维度，还有一个问题需要解决。考虑三维降到二维问题。与之前相同，我们希望找到一个方向是得投影后方差最大，这样就完成了第一个方向的选择，继而我们选择第二个投影方向。

如果我们还是单纯的只选择方差最大的方向，很明显，这个方向与第一个方向应该是“几乎重合在一起”，显然这样的维度是没有用的。从直观上说，让两个字段尽可能的表示更多的原始信息。我们是不希望他们之间存在（线性）相关性的，因为相关性意味着两个字段不是完全独立，必然存在重复表示的信息

数学上可以用两个字段的协方差表示其相关性

我们得到了降维问题的优化目标：将一组N为向量降为K维（K大于0，小于N），其目标是选择K个单位（模为1）正交基，是得原始数据变换到这组基上后，个字段两两之间协方差为0，而字段的方差则尽可能大（在正交的约束下，取最大的K个方差）

• 协方差矩阵

设我们有m个n维数据记录，将其按列排成n乘m的矩阵X，设C=(1/m)X*X^T，则C是一个对称矩阵，其对角线分别是各个字段的方差，而第i行j列和j行i列元素相同，表示i和j两个字段的协方差

• 求C的特征值和特征向量

C的特征值是Y每位元素的方差，也就是D（对角矩阵）的对角线元素

2.2 稀疏编码（Sparse Coding）

（1）概念

• 给定一组N个输入向量x^1,..., x^n，其稀疏编码的目标函数定义为：

  

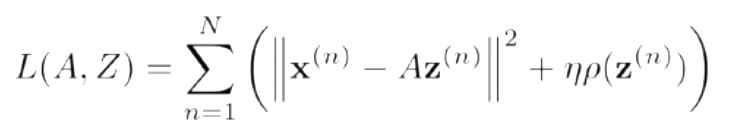
  ρ(·)是一个稀疏性衡量函数，η是一个超参数，用来控制稀疏性的强度

（2）训练过程

• 稀疏编码的训练过程一般用交替优化的方法进行

  1. 固定基向量A，对每个输入x^n,计算其对应的最优编码

     

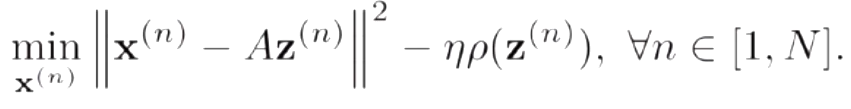
  2. 固定上一步得到的编码z^1,...., z^n，计算其最优的基向量

     

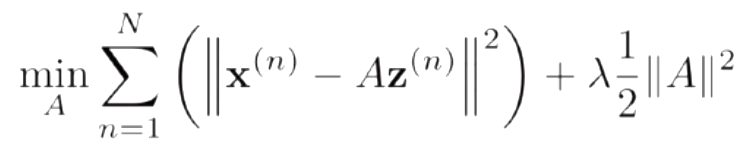
（3）稀疏编码的优点

• 计算量

  稀疏性带来的最大好处就是可以极大地降低计算量

• 可解释性

  因为稀疏编码只有少数的非零元素，相当于将一个输入样本表示为少数几个相关的特征。这样我们可以更好地描述其特征，并易于理解

• 特征选择

  稀疏性带来的另外一个好处是可以实现特征的自动选择，只选择输入样本相关的最后少特征，从而可以更好地表示输入样本，降低噪声并减轻过拟合

3、自编码器（Auto-Encoder）

3.1 概念

模型

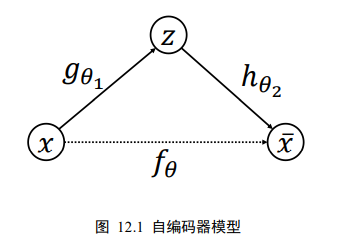
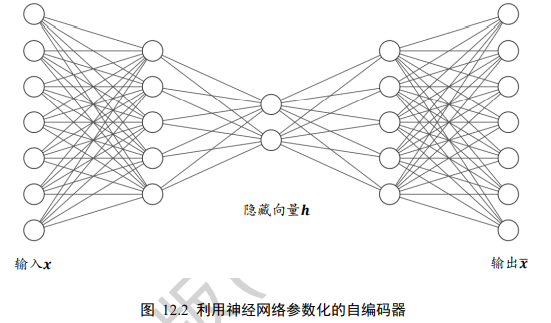
我们把网络fθ切分为2个部分，前面的子网络尝试学习映射关系：gθ1：x->z,后面的字网络尝试学习映射关系hθ2：z->x，我们把gθ1看成一个数据编码（Encode）的过程，把高维度的输入x编码成低纬度的隐变量z（或隐藏变量），成为Encoder网络（编码器）；hθ2看成数据解码（Decode）的过程，把编码过后的输入z解码为高维度的x，成为Decoder（解码器）

编码器和解码器共同完成了输入数据x的编码和解码过程，我们把整个网络模型fθ叫做自动编码器（Auto-Encoder），简称自编码器。如果都使用深层神经网络来参数化gθ1和hθ2函数，则称为深度自编码器。如下图：

3.2 实战

# 引入环境
import tensorflow as tf
import numpy as np
from tensorflow import keras
import matplotlib.pyplot as plt
from PIL import Image #pip install pillow
tf.__version__

# 参数初始化
image_size=28*28
h_dim=20
num_epochs=50
batch_size=100
learning_rate=1e-3
new_dim=Image.new('L',(280,280))

# 1.读取数据

(x_train,y_train),(x_test,y_test)=keras.datasets.mnist.load_data()

# 将值变到0-1之间
x_train,x_test=x_train.astype(np.float32)/255.,x_test.astype(np.float32)/255.

# 不需要y
train_db=tf.data.Dataset.from_tensor_slices(x_train)
train_db=train_db.shuffle(batch_size*5).batch(batch_size)

test_db=tf.data.Dataset.from_tensor_slices(x_test)
test_db=test_db.batch(batch_size)

#2。构建网络模型
class AE(keras.Model):
       #   自编码器模型
       def __init__(self):
              super().__init__()
              # 创建Encoder网络
              self.encoder=keras.Sequential([
                     keras.layers.Dense(256,activation='relu'),
                     keras.layers.Dense(128,activation='relu'),
                     keras.layers.Dense(h_dim)
              ],name='encoder')

              # 创建Decoder网络
              self.decoder=keras.Sequential([
                     keras.layers.Dense(128,activation='relu'),
                     keras.layers.Dense(256,activation='relu'),
                     keras.layers.Dense(image_size)                               
                  ],name='decoder')

       def call(self,inputs,traning=None,mask=None):
              # 编码
              h=self.encoder(inputs)
              # 解码
              x_hat=self.decoder(h)
              return x_hat
        
model=AE()
model.build(input_shape=(None,image_size))
model.summary()

# 3.训练网络
for epoch in range(num_epochs):
       for step,x in enumerate(train_db):
              x=tf.reshape(x,[-1,784])
              with tf.GradientTape() as tape:
                     # 前向传播
                     x_reconstruction_logits=model(x)
                     # 计算loss
                     reconstruction_loss=tf.nn.sigmoid_cross_entropy_with_logits(labels=x,logits=x_reconstruction_logits)
                     reconstruction_loss=tf.reduce_mean(reconstruction_loss)
              # 自动求导
              gradients=tape.gradient(reconstruction_loss,model.trainable_variables)
              # 自动更新
              tf.optimizers.Adam(learning_rate).apply_gradients(zip(gradients,model.trainable_variables))

              if step%100==0:
                     print("Epoch:",epoch," ,Step:",step," ,Loss",float(reconstruction_loss) )
        # 每次迭代完成以后，构建图片并比较
       out_logits=model(x[:batch_size // 2])
       out=tf.nn.sigmoid(out_logits) # out is just logits,use sigmoid
       out=tf.reshape(out,[-1,28,28]).numpy()*255

       x=tf.reshape(x[:batch_size//2],[-1,28,28])

       x_concat=tf.concat([x,out],axis=0).numpy()*255.
       x_concat=x_concat.astype(np.uint8)
       
    index=0
       for i in range(0,280,28):
              for j in range(0,280,28):
                     im=x_concat[index]
                     im=Image.fromarray(im,mode='L')
                     new_dim.paste(im,(i,j))
                     index+=1
       
       new_dim.save('images/ae_reconstructed_epoch_%d.png' % (epoch))

       plt.imshow(np.asarray(new_dim))
       plt.show()
       print('New images saved! ')
    
# 4.重建图片

# 取测试集中一个批次的图片
x=next(iter(test_db))
x.shape

x_flatten=tf.reshape(x,[-1,784])
x_hat=model(x_flatten)
x_hat=tf.nn.sigmoid(x_hat)
x_hat=tf.reshape(x_hat,[-1,28,28])
x_hat.shape

# 合并输入图片和输出图片
x_concat=tf.concat([x[:50],x_hat[:50]],axis=0)
x_concat=x_concat.numpy()*255
x_concat=x_concat.astype(np.uint8)
x_concat.shape

# 创建图片阵列
new_im=Image.new('L',(280,280))
index=0
for i in range(0,280,28):
       for j in range(0,280,28):
              im=x_concat[index]
              im=Image.fromarray(im,mode='L')
              new_im.paste(im,(i,j))
              index=index+1
plt.imshow(np.asarray(new_im))

4、自编码器变种

4.1 稀疏自编码器

4.1.1 概念

给自编码器中隐藏层单元z加上稀疏性限制

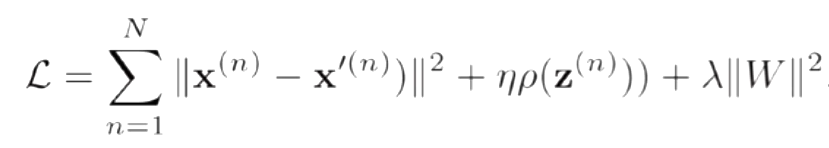
隐藏层的维度大于输入输出层的维度

4.1.2 实战

import tensorflow as tf
import numpy as np
from tensorflow import keras
import matplotlib.pyplot as plt
from PIL import Image #pip install pillow
tf.__version__

image_size=28*28
h_dim=image_size*2
num_epochs=2
batch_size=100
learning_rate=1e-3
new_dim=Image.new('L',(280,280))

rho_star=0.05
lambda_=0.0001
eta=0.001


# 1.读取数据
(x_train,y_train),(x_test,y_test)=keras.datasets.mnist.load_data()

# 将值变到0-1之间
x_train,x_test=x_train.astype(np.float32)/255.,x_test.astype(np.float32)/255.

# 不需要y
train_db=tf.data.Dataset.from_tensor_slices(x_train)
train_db=train_db.shuffle(batch_size*5).batch(batch_size)

test_db=tf.data.Dataset.from_tensor_slices(x_test)
test_db=test_db.batch(batch_size)

# 2.构建网络模型
class SAE(keras.Model):
       #   自编码器模型
       def __init__(self):
              super().__init__()
              # 创建Encoder网络
              self.encoder=keras.Sequential([
                     keras.layers.Dense(256,activation='relu'),
                     keras.layers.Dense(128,activation='relu'),
                     keras.layers.Dense(h_dim)
              ],name='encoder')

              # 创建Decoder网络
              self.decoder=keras.Sequential([
                     keras.layers.Dense(128,activation='relu'),
                     keras.layers.Dense(256,activation='relu'),
                     keras.layers.Dense(image_size)                                         
              ],name='decoder')
        def call(self,inputs,traning=None,mask=None):
              # 编码
              self.h=self.encoder(inputs)
              # 解码
              x_hat=self.decoder(self.h)
              return x_hat
model=SAE()
model.build(input_shape=(None,image_size))
model.summary()

# 3.训练网络
for epoch in range(num_epochs):
       for step,x in enumerate(train_db):
              x=tf.reshape(x,[-1,784])
              with tf.GradientTape() as tape:
                     # 前向传播
                     x_reconstruction_logits=model(x)

                     # 计算loss第一部分
                     sae_loss_1=tf.nn.sigmoid_cross_entropy_with_logits(labels=x,logits=x_reconstruction_logits)
                     # sae_loss_1=tf.reduce_mean(reconstruction_loss)
                     sae_loss_1=tf.reduce_sum(sae_loss_1)/batch_size

                     # 计算loss第二部分
                     w_norm=0
                     for i in range(len(model.trainable_variables)):
                            temp=tf.math.reduce_sum(tf.math.square(model.trainable_variables[i]))
                            w_norm=w_norm+temp
                     sae_loss_2=lambda_*w_norm
                    # 计算loss第三部分
                     rho=tf.math.reduce_mean(model.h,axis=0) # rh0(1568,)
                     KL=0
                     for j in range(rho.shape[0]):
                            # KL散度计算公式
                            # KL(rha/rha_hat)=rho*log(rho/tho_hat)+(1-rho)*log((1-rho)/(1-rho_hat))
                            KL=KL+rho_star*tf.math.log(rho_star/(rho[j]))+(1-rho_star)*tf.math.log((1.-rho_star)/(1.-rho[j]))
                     sae_loss_3=eta*KL

                     # 三部分loss求和
                     sae_loss=sae_loss_1+sae_loss_2+sae_loss_3     
                     # 自动求导
              gradients=tape.gradient(sae_loss,model.trainable_variables)
              # 自动更新
              tf.optimizers.Adam(learning_rate).apply_gradients(zip(gradients,model.trainable_variables))

              if step%100==0:
                     print("Epoch:",epoch," ,Step:",step," ,Loss",float(sae_loss) )


       # 每次迭代完成以后，构建图片并比较
       out_logits=model(x[:batch_size // 2])
       out=tf.nn.sigmoid(out_logits) # out is just logits,use sigmoid
       out=tf.reshape(out,[-1,28,28]).numpy()*255

       x=tf.reshape(x[:batch_size//2],[-1,28,28])

       x_concat=tf.concat([x,out],axis=0).numpy()*255.
       x_concat=x_concat.astype(np.uint8)
       index=0
       for i in range(0,280,28):
              for j in range(0,280,28):
                     im=x_concat[index]
                     im=Image.fromarray(im,mode='L')
                     new_dim.paste(im,(i,j))
                     index+=1
       
       new_dim.save('images/ae_reconstructed_epoch_%d.png' % (epoch))

       plt.imshow(np.asarray(new_dim))
       plt.show()
       print('New images saved! ')
    
# 4.重建图片
# 取测试集中一个批次的图片
x=next(iter(test_db))
x.shape

x_flatten=tf.reshape(x,[-1,784])
x_hat=model(x_flatten)
x_hat=tf.nn.sigmoid(x_hat)
x_hat=tf.reshape(x_hat,[-1,28,28])
x_hat.shape

# 合并输入图片和输出图片
x_concat=tf.concat([x[:50],x_hat[:50]],axis=0)
x_concat=x_concat.numpy()*255
x_concat=x_concat.astype(np.uint8)
x_concat.shape

# 创建图片阵列
new_im=Image.new('L',(280,280))
index=0
for i in range(0,280,280):
       im=x_concat[index]
       im=Image.fromarray(im,model='L')
       new_im.paste(im,(i,j))
       index=index+1
plt.imshow(np.asarray(new_im))

4.2 变分自编码器（VAE）

4.2.1 概念

给定隐藏变量的分布p(z),如果可以学习到条件概率p(x|z),则通过对联合概率分布p(x,z)=p(x|z),p(z)进行采样，生成不同的样本。

如图是VAE模型结构图

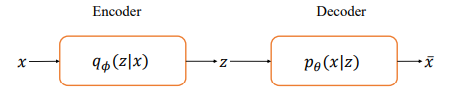
从神经网络的角度来看，VAE相对于自编码器模型，同样具有编码器和解码器两个子网络。解码器接受输入x，输出为隐变量z；解码器负责将隐变量z解码为重建的x冒。不同的是，VAE模型对隐变量z的分布有显式地约束，希望隐变量z符合预设的先验分布p(z)。因此，在损失函数的设计上，除了原有的重建误差项外，还添加了隐变量z分布的约束项。

4.2.2 Reparameterization Trick(重参数化技巧)

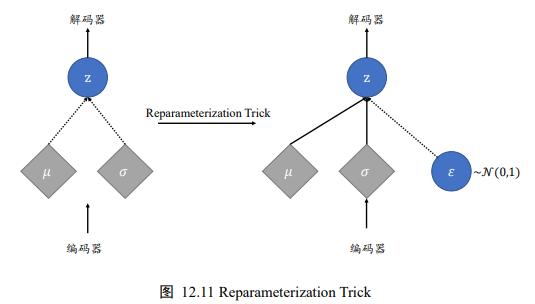
隐变量z采样自编码器的输出qΦ(z|x)，如上图所示，编码器输出正态分布的均值μ和方差σ^2 ，解码器的输入采样自N(μ,σ^2)。由于采样操作的存在，导致梯度传播是不连续的，无法通过梯度下降算法端到端式训练VAE网络。Reparameterization Trick就是论文中提出解决该问题的。

4.2.3 实战

import tensorflow as tf
import numpy as np
from tensorflow import keras
import matplotlib.pyplot as plt
from PIL import Image #pip install pillow
tf.__version__

image_size=28*28
h_dim= 512
z_dim=20
num_epochs=10
batch_size=100
learning_rate=1e-3
new_im=Image.new('L',(280,280))

# 1、读取数据
(x_train,y_train),(x_test,y_test)=keras.datasets.mnist.load_data()

# 将值变到0-1之间
x_train,x_test=x_train.astype(np.float32)/255.,x_test.astype(np.float32)/255.

# 不需要y
train_db=tf.data.Dataset.from_tensor_slices(x_train)
train_db=train_db.shuffle(batch_size*5).batch(batch_size)

test_db=tf.data.Dataset.from_tensor_slices(x_test)
test_db=test_db.batch(batch_size)

# 2、构建网络模型
class VAE(keras.Model):
       #   变分自编码器模型
       def __init__(self):
              super().__init__()
              # 创建Encoder网络
              self.encoder_fc1=tf.keras.layers.Dense(h_dim,activation='relu')
              # μ
              self.encoder_fc_mu=tf.keras.layers.Dense(z_dim)
              # σ^2
              self.encoder_fc_log_var=tf.keras.layers.Dense(z_dim)

              # 创建Decoder网络
              self.decoder=keras.Sequential([
                     keras.layers.Dense(h_dim,activation='relu'),
                     keras.layers.Dense(image_size)                                         
              ],name='decoder')
            # 重参数化技巧
       def reparameterize(self,z_mean,z_log_var):
              # σ
              epsilon=tf.random.normal(z_mean.shape)
              return z_mean+epsilon*tf.exp(z_log_var*0.5) 

       def call(self,inputs,traning=None,mask=None):
              # 编码
              h=self.encoder_fc1(inputs)
              mu=self.encoder_fc_mu(h)
              log_var=self.encoder_fc_log_var(h)
              z=self.reparameterize(mu,log_var)
              # 解码
              x_hat=self.decoder(z)
              return x_hat,mu,log_var
model=VAE()
model.build(input_shape=(batch_size,image_size))
model.summary()

# 3、训练网络
for epoch in range(num_epochs):
       for step,x in enumerate(train_db):
              # x:[100:28:28]
              x=tf.reshape(x,[-1,784])
              with tf.GradientTape() as tape:
                     # 前向传播
                     x_reconstruction_logits,mu,log_var=model(x)
                     # 计算loss第一部分
                     reconstruction_loss=tf.nn.sigmoid_cross_entropy_with_logits(labels=x,logits=x_reconstruction_logits)
                     # sae_loss_1=tf.reduce_mean(reconstruction_loss)
                     reconstruction_loss=tf.reduce_sum(reconstruction_loss)/batch_size

                     # 计算loss第二部分
                     kl_div=-0.5*tf.reduce_sum(1.+log_var-tf.square(mu)-tf.exp(log_var),axis=1)
                     kl_div=tf.reduce_mean(kl_div)
              
                     # 两部分loss求和
                     loss=reconstruction_loss+kl_div  
                    # 自动求导
              gradients=tape.gradient(loss,model.trainable_variables)
              # 自动更新
              tf.optimizers.Adam(learning_rate).apply_gradients(zip(gradients,
model.trainable_variables))
              if step%100==0:
                     print("Epoch:",epoch," ,Step:",step," ,Loss",float(loss),
                     " rec_loss:",float(reconstruction_loss)," kl_div:",float(kl_div) )

       # 每次迭代完成以后，构建图片并比较
       out_logits,_,_=model(x[:batch_size // 2])
       out=tf.nn.sigmoid(out_logits) # out is just logits,use sigmoid
       out=tf.reshape(out,[-1,28,28]).numpy()*255
        x=tf.reshape(x[:batch_size//2],[-1,28,28])

       x_concat=tf.concat([x,out],axis=0).numpy()*255.
       x_concat=x_concat.astype(np.uint8)

       index=0
       for i in range(0,280,28):
              for j in range(0,280,28):
                     im=x_concat[index]
                     im=Image.fromarray(im,mode='L')
                     new_dim.paste(im,(i,j))
                     index+=1
       
       new_im.save('images/ae_reconstructed_epoch_%d.png' % (epoch))

       plt.imshow(np.asarray(new_im))
       plt.show()
       print('New images saved! ')

# 4、重建图片
# 取测试集中一个批次的图片
x=next(iter(test_db))
x.shape

x_flatten=tf.reshape(x,[-1,784])
x_hat,_,_=model(x_flatten)
x_hat=tf.nn.sigmoid(x_hat)
x_hat=tf.reshape(x_hat,[-1,28,28])
x_hat.shape

# 合并输入图片和输出图片
x_concat=tf.concat([x[:50],x_hat[:50]],axis=0)
x_concat=x_concat.numpy()*255
x_concat=x_concat.astype(np.uint8)
x_concat.shape

# 创建图片阵列
new_im=Image.new('L',(280,280))
index=0
for i in range(0,280,280):
       im=x_concat[index]
       im=Image.fromarray(im,model='L')
       new_im.paste(im,(i,j))
       index=index+1
plt.imshow(np.asarray(new_im))
    
    

第九章 生成对抗网络

生成对抗网络：Generative Adversarial Networks

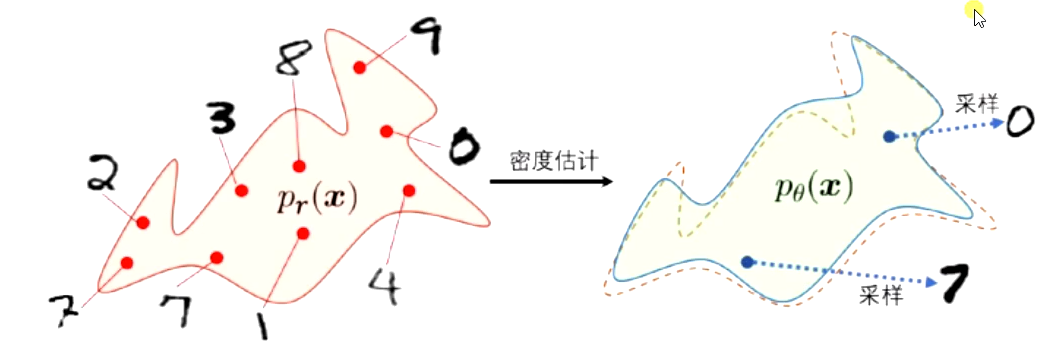
1、密度模型

1.1 显式密度模型

显式的构建出样本的密度函数p(x|θ)，并通过最大似然估计来求解参数

变分自编码器、深度信念网络

生成模型包含两个步骤 ：

• 密度估计

• 采样

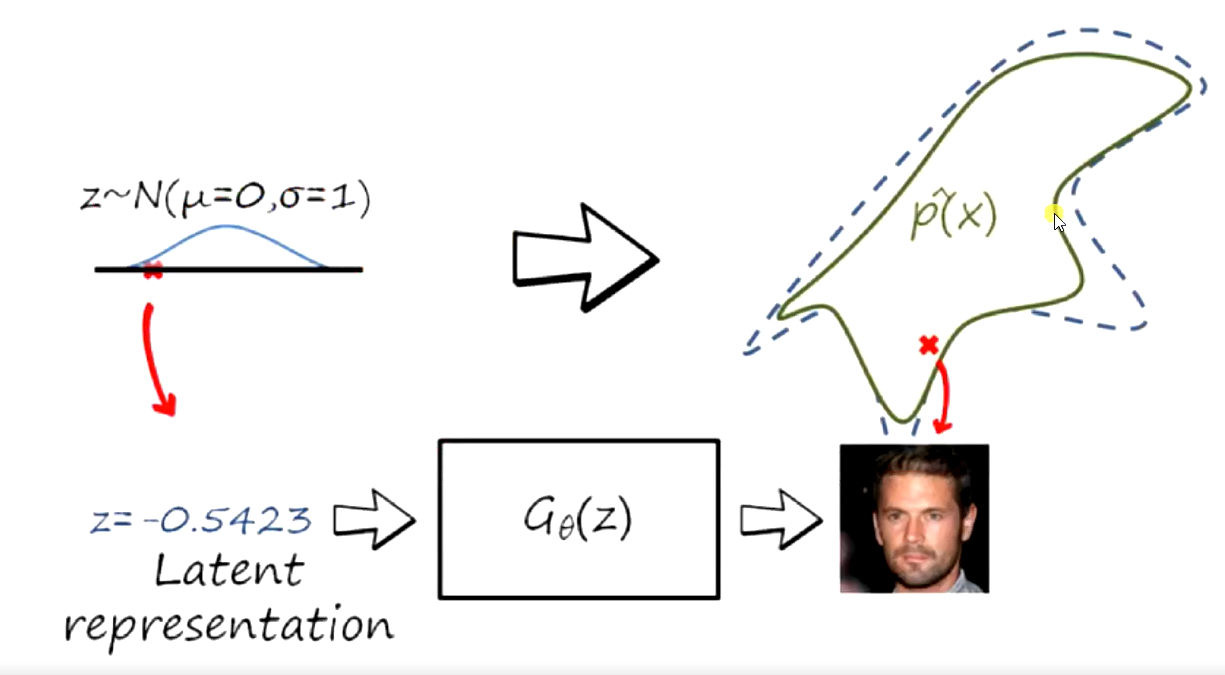
1.2 隐式密度模型

不显式的估计出数据分布的密度函数

但能生成符合数据分布Pdata(x)的样本

无法用最大似然估计

生成模型

2、生成对抗网络模型

2.1 GAN对抗过程：博弈学习

印钞机：生成模型

验钞机：判别模型

目标：使得判别器无法判断，无论对于真假样本，输出结果概率都是0.5

2.2 生成网络

生成网络从潜在空间中随机采样作为输入，其输出结果需要尽量模仿训练集中的真实样本

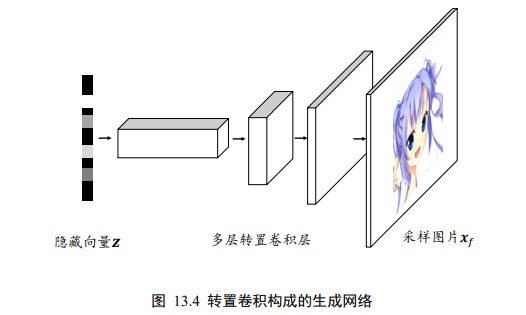
2.3 判别网络

判别网络的输入则为真实样本或生成网络的输出，其目的是将生成网络的输出从真实样本中尽可能分辨出来

2.4 对抗训练

生成网络要尽可能地欺骗判别网络

判别网络将生成网络生成的样本与真实样本中尽可能区分出来

两个网络相互对抗、不断调整参数，最终目的是使判别网络无法判断生成网络的输出结果是否真实

2.5 网络训练

2.5.1 对于判别网络

判别网络将生成网络生成的样本与真实样本中尽可能区分出来，它的目标是最小化图片的预测值和真实值之间的交叉熵损失函数：

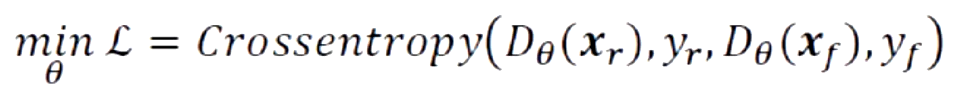
2.5.2 对于生成网络

我们希望xf=G(z)能够很好的骗过判别网络D，假样本xf在判别网络的输出越接近真是的标签越好。也就是说，在训练生成网络时，希望判别网络的输出D(G(z))越逼近1越好，此时的交叉熵损失函数为：

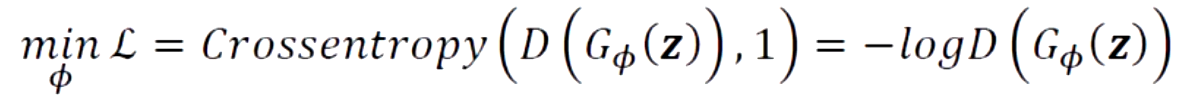
2.5.3 统一目标函数

我们把判别网络的目标和生成网络的目标合并，并写成min-max博弈形式：

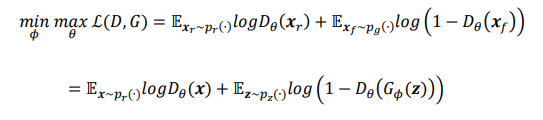
2.6 GAN的代码实战

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from tensorflow import keras
tf.__version__

LENGTH=100
batch_size=20
z_len=20
lr=0.001
EPOCHS=100
k=5

np.random.seed(0)
# 创建20组正态分布的数据，每组100个数据
def create_real_data(num_data=20,len=100):
       data=[]
       for _ in range(num_data):
              # 均值为4，方差1.5，每组共100个数据
              data.append(np.random.normal(4,1.5,len))
       return np.array(data)

np.random.seed(0)
# z数据，随机
# 创建20组正态分布的数据，每组100个数据
def create_random_data(num_data=20,len=20):
       data=[]
       for _ in range(num_data):
              # 均值为4，方差1.5，每组共100个数据
              data.append(np.random.random(len))
       return np.array(data)

real_data=create_real_data()
plt.plot(real_data[0])

(data,bins)=np.histogram(real_data[0])
plt.plot(bins[:-1],data)

data,bins

# 构建生成器
class Generate(keras.Model):
       def __init__(self):
              super().__init__()
              self.FC1=keras.layers.Dense(32,activation="relu")
              self.FC2=keras.layers.Dense(32,activation="sigmoid")
              self.FC3=keras.layers.Dense(LENGTH)

       def call(self,inputs):
              x=self.FC1(inputs)
              print(x)
              x=self.FC2(x)
              print(x)
              x=self.FC3(x)
              print(x)
              return x
        
generator=Generate()
generator.build(input_shape=(None,z_len))
generator.summary()
g_optimizer=keras.optimizers.Adam(lr)

# 构建判别器
class Discriminator(keras.Model):
       def __init__(self):
              super().__init__()
              self.FC1=keras.layers.Dense(32,activation="relu")
              self.FC2=keras.layers.Dense(32,activation="sigmoid")
              self.FC3=keras.layers.Dense(1)

       def call(self,inputs):
              x=self.FC1(inputs)
              print(x)
              x=self.FC2(x)
              print(x)
              x=self.FC3(x)
              print(x)
              return x
        
discriminator=Discriminator()
discriminator.build(input_shape=(None,LENGTH))
discriminator.summary()
d_optimizer=keras.optimizers.Adam(lr)

z=create_real_data(batch_size,z_len)

(data_,bins_)=np.histogram(z[0])
plt.plot(bins[:-1],data)
plt.plot(bins_[:-1],data_)

# 和1比
def loss_ones(logits):
       loss=keras.losses.binary_crossentropy(logits,tf.ones_like(logits),from_logits=True)
       return tf.reduce_mean(loss)

# 和0比
def loss_zeros(logits):
       loss=keras.losses.binary_crossentropy(logits,tf.zeros_like(logits),from_logits=True)
       return tf.reduce_mean(loss)

def D_loss(generator,discriminator,batch_z,batch_x):
       # 生成假样本
       fake_data=generator(batch_z)
       # 判断假样本
       d_fake_logtis=discriminator(fake_data)
       # 假样本的logits和0比
       d_loss_fake=loss_zeros(d_fake_logtis)

       
       # 判断真样本
       d_real_logtis=discriminator(batch_x)
       # 真样本的logits和1比
       d_loss_real=loss_ones(d_real_logtis)

       # 合并
       d_loss=d_loss_fake+d_loss_real
       return d_loss

def G_loss(generator,discriminator,batch_z):
       # 生成假样本
       fake_data=generator(batch_z)
       # 判断假样本
       g_fake_logtis=discriminator(fake_data)
       # 假样本的logits和1比
       g_loss_fake=loss_ones(g_fake_logtis)

       return g_loss_fake
    
# 训练
batch_z=create_random_data()
batch_x=real_data
d_loss_history=[]
g_loss_history=[]
loss_history=[]
for epoch in range(EPOCHS):
       for _ in range(k):
              with tf.GradientTape() as tape:
                     d_loss=D_loss(generator,discriminator,batch_z,batch_x)
              d_grads=tape.gradient(d_loss,discriminator.trainable_variables)
              d_optimizer.apply_gradients(zip(d_grads,discriminator.trainable_variables))
       
       with tf.GradientTape() as tape:
              g_loss=G_loss(generator,discriminator,batch_z)
       g_grads=tape.gradient(g_loss,generator.trainable_variables)
       g_optimizer.apply_gradients(zip(g_grads,generator.trainable_variables))
       
       d_loss_history.append(d_loss)
       g_loss_history.append(g_loss)
       loss_history.append(d_loss+g_loss)


       if epoch%100==0:
              print("epoch: ",epoch,"loss:",d_loss+g_loss)
              z=create_random_data()
              fake_data=generator(z)
              (data__,bins__)=np.histogram(fake_data[0])
              plt.plot(bins[:-1],data)
              plt.plot(bins__[:-1],data__)
              plt.show()
            
z=create_random_data()
fake_data=generator(z)
(data__,bins__)=np.histogram(fake_data[0])
plt.plot(bins[:-1],data)
plt.plot(bins__[:-1],data__)
plt.show()

plt.plot(d_loss_history)

plt.plot(g_loss_history)

plt.plot(loss_history)

3、DCGAN

DCGAN：Deep Convolution Generative Adversarial Networks

3.1 设计原则

• 在生成器和判别器特征提取层用卷积神经网络代替了原始GAN中的多层感知机（且将传统cnn中池化层用卷积层代替）
• 去除全连接层（参数量大）
• 使用批归一化Batch Normalization（加快网络的训练和收敛的速度控制梯度爆炸，防止梯度消失防止过拟合）
• 使用恰当的激活函数（tanh，sigmoid，relu，leakyrelu）

3.2 网络结构

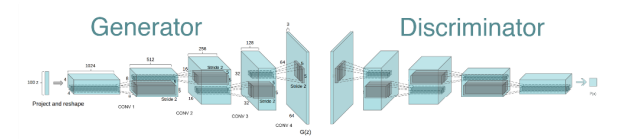
3.2.1 对于生成器

• 使用转置（反）卷积：
  • 上采样（Upsample）：实现图像由小分辨率到大分辨率的映射的操作
  • 反卷积（Transposed Convolution）：先按照一定的比例通过补0来扩大输入图像的尺寸，接着旋转卷积核，再进行正向卷积

3.3 实战

import tensorflow as tf
from tensorflow import keras
import matplotlib.pyplot as plt 
import numpy as np 
from tensorflow.keras import layers
tf.__version__

# 1、读取MNIST数据集
z_length=10
batch_size=256
learning_rate=0.0002
epochs=50

(x_train,y_train),(x_test,y_test)=tf.keras.datasets.mnist.load_data()
x_train.shape
x_train[0].shape

plt.figure(figsize=(4,4)) # 设置图片大小
for i in range(1,17):     # 编号从1开始
       plt.subplot(4,4,i)
       plt.imshow(x_train[i-1],cmap=plt.cm.gray) # 显示16张图片（灰度图）
       plt.xticks([]) # 去除坐标
       plt.yticks([]) # 去除坐标
plt.show()

def preprocess(x):
       x=(tf.cast(x,dtype=tf.float32)/255.-0.5)*2
       x=tf.reshape(x,[-1,28,28,1])
       return x
    
dataset=tf.data.Dataset.from_tensor_slices(x_train).shuffle(60000).batch(batch_size).map(preprocess)

# 2、Generator的网络结构
def make_generator_model():
       model=tf.keras.Sequential()
       model.add(layers.Dense(7*7*256,use_bias=False))
       model.add(layers.BatchNormalization())
       model.add(layers.LeakyReLU())

       model.add(layers.Reshape((7,7,256)))

       model.add(layers.Conv2DTranspose(128,(5,5),strides=(1,1),padding='same',use_bias=False))
       model.add(layers.BatchNormalization())
       model.add(layers.LeakyReLU())

       model.add(layers.Conv2DTranspose(64,(5,5),strides=(2,2),padding='same',use_bias=False))
       model.add(layers.BatchNormalization())
       model.add(layers.LeakyReLU())

       model.add(layers.Conv2DTranspose(1,(5,5),strides=(2,2),padding='same',use_bias=False,activation='tanh'))

       return model
    
# 创建生成器网络
generator=make_generator_model()

#[batch_size,z_length]
generator.build(input_shape=(batch_size,z_length))

# 构造优化器
generator_optimizer=keras.optimizers.Adam(learning_rate)

# 生成器网络结构
generator.summary()

# 3、Discriminator的网络结构
def make_discriminator_model():

       model=tf.keras.Sequential()
       model.add(layers.Conv2D(64,(5,5),strides=(2,2),padding='same'))
       model.add(layers.LeakyReLU())
       model.add(layers.Dropout(0.3))
       
       model.add(layers.Conv2D(128,(5,5),strides=(2,2),padding='same'))
       model.add(layers.LeakyReLU())
       model.add(layers.Dropout(0.3))

       model.add(layers.Flatten())
       model.add(layers.Dense(1,activation='sigmoid'))

       return model
    
# 创建判别器网络
discriminator=make_discriminator_model()
discriminator.build(input_shape=(batch_size,28,28,1))

# 构造优化器
discriminator_optimizer=keras.optimizers.Adam(learning_rate)
# 判别网络器结构
discriminator.summary()

# 4、训练与可视化
# 4.1 判断网络
判断网络的训练目标是最大化L(D,G),使得真实样本预测为真的概率接近1，生成样本预测为真的概率接近0

def random_data(batch_size=batch_size,length=z_length):
       # 随机生成长度为z_length的batch_size个噪声数据（生成器的初始化分布）
       return tf.random.normal([batch_size,length])

# 生成噪声数据，输入到生成器中，得到一张无意义的图片
z=random_data(batch_size,z_length)
fake_data=generator(z)
fake_data.shape

# 此时的初级判别器对生成器生成的图片做的判断
discriminator(fake_data).numpy()[:5]

# 展示无意义图片
fake_data=tf.reshape(fake_data,(-1,28,28))
plt.figure(figsize=(4,4)) #设置图片大小
for i in range(1,17):     # 编号从1开始
       plt.subplot(4,4,i)
       plt.imshow(fake_data[i-1],cmap=plt.cm.gray) # 显示16张图片（灰度图）
       plt.xticks([]) # 去除坐标
       plt.yticks([]) # 去除坐标
plt.show()

cross_entropy=tf.keras.losses.BinaryCrossentropy(from_logits=False)

def generator_loss(fake_output):
       return cross_entropy(tf.ones_like(fake_output),fake_output)


def discriminator_loss(real_output,fake_output):
       real_loss=cross_entropy(tf.ones_like(real_output),real_output)
       fake_loss=cross_entropy(tf.zeros_like(fake_output),fake_output)
       total_loss=real_loss+fake_loss
       return total_loss

# 4.2 生成对抗网络
最小化L(G,D)，无需考虑真实数据。可以将生成数据样本标注为1，最小化此时的交叉熵误差

# 5、训练

d_loss_history=[]
g_loss_history=[]
loss_history=[]

# 梯度下降、反向传播更新模型参数
@tf.function
def train_step(batch_x):
       batch_z=tf.random.normal([batch_size,z_length])
       # 梯度下降
       with tf.GradientTape() as gen_tape,tf.GradientTape() as disc_tape:
              # 生成器生成假图片
              generated_images=generator(batch_z,training=True)
              # 判别器判定生成图片真假
              fake_output=discriminator(generated_images,training=True)
              # 判别器判定真实图片真假
              real_output=discriminator(batch_x,training=True)
              # 计算生成器loss
              gen_loss=generator_loss(fake_output)
              # 计算判别器loss
              disc_loss=discriminator_loss(real_output,fake_output)

       # 计算生成器梯度
       gradient_of_generator=gen_tape.gradient(gen_loss,generator.trainable_variables)
       # 计算判别器梯度
       gradient_of_discriminator=disc_tape.gradient(disc_loss,discriminator.trainable_variables)

       # 更新梯度
       generator_optimizer.apply_gradients(zip(gradient_of_generator,generator.trainable_variables))
       discriminator_optimizer.apply_gradients(zip(gradient_of_discriminator,discriminator.trainable_variables))

       return gen_loss,disc_loss
    
# 训练
for epoch in range(epochs):
       for batch_x in dataset:
              gen_loss,disc_loss=train_step(batch_x)
              d_loss_history.append(disc_loss.numpy())
              g_loss_history.append(gen_loss.numpy())
              loss_history.append(disc_loss.numpy()+gen_loss.numpy())

       if epoch%5==0:
              # 输出loss
              print('epoch:',epoch,'gen_loss:',gen_loss.numpy(),'disc_loss:',disc_loss)

              # 采样图示 真实数据与生成器生成数据
              batch_z=tf.random.normal([batch_size,z_length])
              fake_data=generator(batch_z)
              # 显示图片
              plt.figure(figsize=(4,4)) #设置图片大小
              fake_data=tf.reshape(fake_data,(-1,28,28))
              for i in range(1,17):     # 编号从1开始
                     plt.subplot(4,4,i)
                     plt.imshow(fake_data[i-1]*127.5+127.5,cmap=plt.cm.gray) # 显示128张图片（灰度图）
                     plt.xticks([]) # 去除坐标
                     plt.yticks([]) # 去除坐标
              plt.show()
            
# 判别器loss的变化曲线
plt.plot(d_loss_history)

# 生成器loss的变化曲线
plt.plot(g_loss_history)

# loss的变化曲线
plt.plot(loss_history)

tf.random.set_seed(1)
z=random_data(1,length=z_length)
z=z.numpy()
z[:,0]=4
z

4、GAN训练难题

4.1 超参数敏感

超参数敏感是指网络的结构设定、学习率、初始化状态等超参数对网络的训练过程影响较大，微量的超参数调整可能导致网络的训练结果截然不同

4.2 模式崩塌

模式崩塌是指模型生成的样本单一，多样性很差。由于判别器只能鉴别单个样本是否采样自真实样本，并没有对样本多样性进行显式约束，导致生成模型可能倾向于生成真实分布的部分区间中的少量高质量样本，以此来在判别器的输出中获得较高的概率值

5、WGAN原理

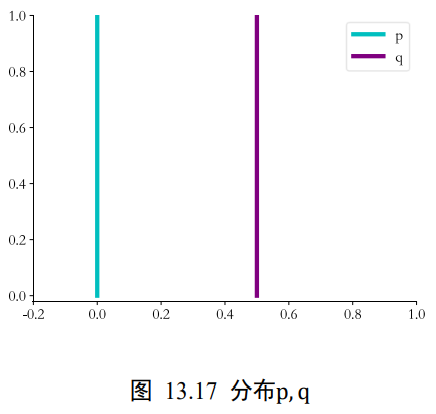
WGAN算法从理论层面分析了GAN训练不稳定的原因，并提出了有效的解决方案。那是什么原因导致了GAN训练如此不稳定？WGAN提出是因为JS散度在不重叠的分布p和q上的梯度曲面是恒定为0的。如下图，当分布p和q不重叠时，JS散度的梯度值始终为0，从而导致此时GAN的训练出现梯度弥散的现象，参数长时间得不到更新，网络无法收敛。

5.1 EM距离

WGAN论文发现了JS散度导致GAN训练不稳定的问题，并引入了一种新的分布距离度量方法：Wasserstein距离，也叫推土机距离（Earth-Mover Distance，简称EM距离），他表示了从一个分布变换到另一个分布的最小代价，定义为：

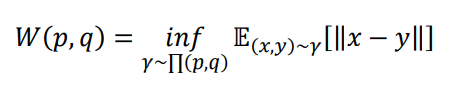
其中Π(p,q)是分布p,q组合起来的所有可能的联合分布的集合，对于每个可能的联合分布γ~Π(p,q)，计算距离||x-y||的期望E(x,y)[||x-y||]，其中(x,y)采样自联合分布γ。不同的联合分布γ有不同的期望E(x,y)[||x-y||]，这些期望中的下确界即定义为分布p,q的Wasserstein距离。

5.2 实战

import tensorflow as tf
from tensorflow import keras
import matplotlib.pyplot as plt 
import numpy as np 
from tensorflow.keras import layers
tf.__version__

# 1、读取MNIST数据集
z_length=10
batch_size=128
learning_rate=0.0002
epochs=20

# mean=0.0,stddev=0.05,seed=None
init=tf.keras.initializers.RandomNormal(stddev=0.02)

(x_train,y_train),(x_test,y_test)=tf.keras.datasets.mnist.load_data()
x_train.shape
x_train[0].shape

plt.figure(figsize=(4,4)) # 设置图片大小
for i in range(1,17):     # 编号从1开始
       plt.subplot(4,4,i)
       plt.imshow(x_train[i-1],cmap=plt.cm.gray) # 显示16张图片（灰度图）
       plt.xticks([]) # 去除坐标
       plt.yticks([]) # 去除坐标
plt.show()

def preprocess(x):
       x=(tf.cast(x,dtype=tf.float32)/255.-0.5)*2
       x=tf.reshape(x,[-1,28,28,1])
       return x
    
dataset=tf.data.Dataset.from_tensor_slices(x_train).shuffle(60000).batch(batch_size,drop_remainder=True).map(preprocess)

def make_generator_model():
       model=tf.keras.Sequential()

       # FC
       # 第一层
       # 增加参数初始化
       # 使用bias

       model.add(layers.Dense(7*7*512,kernel_initializer=init))
       model.add(layers.Reshape((7,7,512)))

       # 第2层
       # kernel  5->3  stride 1->2
       # 使用bias
       # momentum 0.99->0.8
       # LeakyReLU ->relu
       # Relu最大值0.2
       model.add(layers.Conv2DTranspose(128,(3,3),strides=(2,2),padding='same'))
       model.add(layers.BatchNormalization(momentum=0.8))
       model.add(layers.ReLU(0.2))

       # 第3层
       # kernel  5->3  stride 2->1
       # 使用bias
       # momentum 0.99->0.8
       # LeakyReLU ->relu
       # Relu最大值0.2
       model.add(layers.Conv2DTranspose(64,(3,3),strides=(1,1),padding='same'))
       model.add(layers.BatchNormalization(momentum=0.8))
       model.add(layers.ReLU())

       # 输出
       # kernel 5->3
       model.add(layers.Conv2DTranspose(1,(3,3),strides=(2,2),padding='same',activation='tanh'))

       return model
    
def make_generator_model():
       model=tf.keras.Sequential()

       # FC
       # 第一层
       # 增加参数初始化
       # 使用bias

       model.add(layers.Dense(7*7*512,kernel_initializer=init))
       model.add(layers.Reshape((7,7,512)))

       # 第2层
       # kernel  5->3  stride 1->2
       # 使用bias
       # momentum 0.99->0.8
       # LeakyReLU ->relu
       # Relu最大值0.2
       model.add(layers.Conv2DTranspose(128,(3,3),strides=(2,2),padding='same'))
       model.add(layers.BatchNormalization(momentum=0.8))
       model.add(layers.ReLU(0.2))

       # 第3层
       # kernel  5->3  stride 2->1
       # 使用bias
       # momentum 0.99->0.8
       # LeakyReLU ->relu
       # Relu最大值0.2
       model.add(layers.Conv2DTranspose(64,(3,3),strides=(1,1),padding='same'))
       model.add(layers.BatchNormalization(momentum=0.8))
       model.add(layers.ReLU())

       # 输出
       # kernel 5->3
       model.add(layers.Conv2DTranspose(1,(3,3),strides=(2,2),padding='same',activation='tanh'))

       return model
    
# 创建生成器网络
generator=make_generator_model()

#[batch_size,z_length]
generator.build(input_shape=(batch_size,z_length))

# 构造优化器
# 不用Adam，改用RMSprop 0.00005
generator_optimizer=keras.optimizers.Adam(learning_rate=0.00005)

# 生成器网络结构
generator.summary()

def make_discriminator_model():

       model=tf.keras.Sequential()

       # 第1层
       # kernel 5->3
       # LeakyReLU alpha=0.2
       # 无dropout
       model.add(layers.Conv2D(64,(3,3),strides=(2,2),padding='same'))
       model.add(layers.LeakyReLU())
       
       # 第2层
       # kernel 5->3
       # LeakyReLU alpha=0.2
       # 增加BatchNormalization
       # 无dropout
       model.add(layers.Conv2D(128,(5,5),strides=(2,2),padding='same'))
       model.add(layers.BatchNormalization(momentum=0.8))
       model.add(layers.LeakyReLU(0.2))

       # 第3层
       # 新增
       model.add(layers.Conv2D(256,(3,3),strides=(2,2),padding='same'))
       model.add(layers.BatchNormalization(momentum=0.8))
       model.add(layers.LeakyReLU(0.2))

       # 第4层
       # 新增
       model.add(layers.Conv2D(512,(3,3),strides=(1,1),padding='same'))
       model.add(layers.BatchNormalization(momentum=0.8))
       model.add(layers.LeakyReLU(0.2))

       # FC
       model.add(layers.Flatten())
       # 输出
       # 去掉sigmoid
       model.add(layers.Dense(1))

       return model

# 创建判别器网络
discriminator=make_discriminator_model()
discriminator.build(input_shape=(batch_size,28,28,1))

# 构造优化器
discriminator_optimizer=keras.optimizers.RMSprop(learning_rate=0.00005)
# 判别网络器结构
discriminator.summary()


# 4、训练与可视化
# 4.1 判断网络
判断网络的训练目标是最大化L(D,G),使得真实样本预测为真的概率接近1，生成样本预测为真的概率接近0

def random_data(batch_size=batch_size,length=z_length):
       # 随机生成长度为z_length的batch_size个噪声数据（生成器的初始化分布）
       return tf.random.normal([batch_size,length])

# 生成噪声数据，输入到生成器中，得到一张无意义的图片
z=random_data(batch_size,z_length)
fake_data=generator(z)
fake_data.shape

# 此时的初级判别器对生成器生成的图片做的判断
discriminator(fake_data).numpy()[:5]

# 展示无意义图片
fake_data=tf.reshape(fake_data,(-1,28,28))
plt.figure(figsize=(4,4)) #设置图片大小
for i in range(1,17):     # 编号从1开始
       plt.subplot(4,4,i)
       plt.imshow(fake_data[i-1]*127.5+127.5,cmap=plt.cm.gray) # 显示16张图片（灰度图）
       plt.xticks([]) # 去除坐标
       plt.yticks([]) # 去除坐标
plt.show()

len(discriminator.trainable_variables)

def Clip(w):
       return tf.clip_by_value(w,-0.01,0.01)
    
# 5、训练

d_loss_history=[]
g_loss_history=[]
loss_history=[]

# @tf.function 提取权重值无法用
def train_step(batch_x):
       # 训练判别器discriminator
       for i in range(5):
              discriminator.trainable=True
              # 固定生成器，优化判别器
              with tf.GradientTape() as tape:
                     # 生成假样本
                     batch_z=tf.random.normal([batch_size,z_length])
                     fake_x=generator(batch_z)
                     d_loss=-tf.reduce_mean(discriminator(batch_x))+tf.reduce_mean(discriminator(fake_x))

              # 计算梯度
              d_grads=tape.gradient(d_loss,discriminator.trainable_variables)
              # 优化
              discriminator_optimizer.apply_gradients(zip(d_grads,discriminator.trainable_variables))
              for layers in discriminator.layers:
                     weights=layers.get_weights()
                     weights=[tf.clip_by_value(w,-0.01,0.01) for w in weights]
                     layers.set_weights(weights)

       # 训练生成器 generator
       # 训练生成器时判别器不动
       discriminator.trainable=False
       with tf.GradientTape() as tape:
              # 生成假样本
              fake_x=generator(batch_z)
              g_loss=-tf.reduce_mean(discriminator(fake_x))
       g_grads=tape.gradient(g_loss,generator.trainable_variables)
       generator_optimizer.apply_gradients(zip(g_grads,generator.trainable_variables))

       return g_loss,d_loss

# 训练
for epoch in range(epochs):
       for index,batch_x in enumerate(dataset):
              # 训练
              g_loss,d_loss=train_step(batch_x)

              # 记录loss
              d_loss_history.append(d_loss)
              g_loss_history.append(g_loss)
              loss_history.append(d_loss+g_loss)

       # 输出loss
       print('epoch:',epoch,'gen_loss:',g_loss,'disc_loss:',d_loss)

       if epoch%1==0:

              # 采样图示 真实数据与生成器生成数据
              batch_z=tf.random.normal([batch_size,z_length])
              fake_data=generator(batch_z)
              # 显示图片
              plt.figure(figsize=(4,4)) #设置图片大小
              fake_data=tf.reshape(fake_data,(-1,28,28))
              for i in range(1,17):     # 编号从1开始
                     plt.subplot(4,4,i)
                     plt.imshow(fake_data[i-1]*127.5+127.5,cmap=plt.cm.gray) # 显示128张图片（灰度图）
                     plt.xticks([]) # 去除坐标
                     plt.yticks([]) # 去除坐标
              plt.show()
            
# 判别器loss的变化曲线
plt.plot(d_loss_history)

# 生成器loss的变化曲线
plt.plot(g_loss_history)

# loss的变化曲线
plt.plot(loss_history)

tf.random.set_seed(1)
z=random_data(1,length=z_length)
z=z.numpy()
z[:,0]=4
z

6、GAN的扩展

6.1 The GAN Zoo

6.2 Conditional GAN

6.3 InfoGAN

6.4 BiGAN

6.5 GAN训练中的炼丹技巧

• 不要纠结于损失函数的选择
• 关于增加模型的容量
• 尝试改变标签
• 尝试使用batch normalization
• 尝试分次训练
• 最好不要提早结束
• 关于k的选择
• 关于学习率增加噪声不要使用性能太好的判别器
• 可以尝试使用最新的multi-scale gradient方法
• 可以尝试使用TTUR
• 使用Spectral Normalization