BST二叉查找树接口设计

BST二叉查找树的接口设计

二叉查找树英文缩写为BST树（Binary Search Tree），一般也被称为二叉搜索树或者二叉排序树，二叉查找树的结点是有键值key的，如果二叉查找树不是空树则需要遵循以下的特点：

1. 如果二叉查找树有左子树，则左子树的结点的键值key要小于左子树的根结点的键值key

2. 如果二叉查找树有右子树，则右子树的结点的键值key要大于右子树的根结点的键值key

3. 对于二叉查找树而言，左子树和右子树也分别是二叉查找树，如下图：

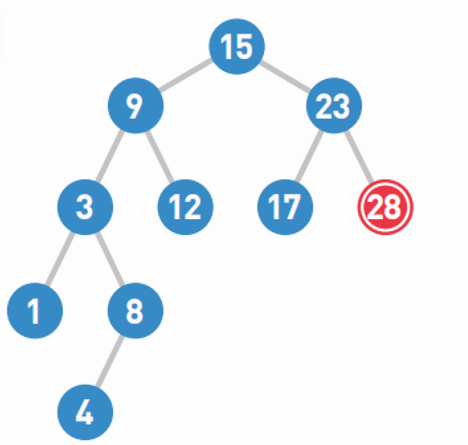
我们可以利用双向不循环链表实现，通过对根节点的比较一直找到叶子节点，进行插入操作，通过递归思想，在遍历的时候根节点变换，由根节点到子树的根节点，不断向下，找到插入的地方。

目录

• BST二叉查找树的接口设计
  • 创建根节点并初始化
  • 新节点创建
  • 插入新节点
  • 主函数测试

创建根节点并初始化

设计BST二叉查找树的接口，为了方便对二叉树进行节点的增删，所以采用双向不循环链表实现,创建一个带根节点的BST树，对BST树的根节点进行初始化

• /*****************************************************************
  *
  *
  * 设计BST二叉查找树的接口，为了方便对二叉树进行节点的增删，所以采用双向不循环链表实现，每个节点内部都需要
  * 有2个指针，分别指向该节点的左子树(lchild)和右子树(rchild)
  *
  * 
  *
  * Copyright (c)  2024-2025   yq_dyx@163.com   All right Reserved
  * *****************************************************************/
  
  
  #include <stdio.h>
  #include <stdlib.h>
  #include <stdbool.h>
  
  #include "drawtree.h"
  
  #if 0
  //指的是BST树中的结点有效键值的数据类型，用户可以根据需要进行修改
  typedef int  DataType_t;
  
  
  //构造BST树的结点,BST树中所有结点的数据类型应该是相同的
  typedef struct BSTreeNode
  {
  	DataType_t  		 data; 	//节点的键值
  	struct BSTreeNode	*lchild; 	//左子树的指针域
  	struct BSTreeNode	*rchild; 	//右子树的指针域
  
  }BSTnode_t;
  #endif
  
   /****************************************************************
    *
    *	name	 :	BSTree_Create
    *	function :  创建一个空树并创建一个根结点，并进行初始化
    *	argument :  
    *	retval	 :  None
    *	author	 :  yq_dyx@163.com
    *	date	 :  2024/05/06
    * note	 :  None
    * 	
    * *****************************************************************/
  //创建一个带根节点的BST树，对BST树的根节点进行初始化
  BSTnode_t * BSTree_Create(DataType_t KeyVal)
  {
  	//1.创建一个根结点并对根结点申请内存
  	BSTnode_t *Root = (BSTnode_t *)calloc(1,sizeof(BSTnode_t));
  	if (NULL == Root)
  	{
  		perror("Calloc memory for Root is Failed");
  		exit(-1);
  	}
  
  	//2.对根结点进行初始化，根节点的2个指针域分别指向NULL
  	Root->data = KeyVal;
  	Root->lchild = NULL;
  	Root->rchild = NULL;
  
  	//3.把根结点的地址返回即可
  	return Root;
  }
  

  新节点创建

  创建新的结点并初始化

   /****************************************************************
    *
    *	name	 :	BSTree_NewNode
    *	function :  创建一个新结点，并进行初始化
    *	argument :  @KeyVal：键值
    *	retval	 :  None
    *	author	 :  yq_dyx@163.com
    *	date	 :  2024/05/06
    * note	 :  None
    * 	
   ****************************************************************/
  //创建新的结点，并对新结点进行初始化（数据域 + 指针域）
  BSTnode_t * BSTree_NewNode(DataType_t KeyVal)
  {
  	//1.创建一个新结点并对新结点申请内存
  	BSTnode_t *New = (BSTnode_t *)calloc(1,sizeof(BSTnode_t));
  	if (NULL == New)
  	{
  		perror("Calloc memory for NewNode is Failed");
  		return NULL;
  	}
  
  	//2.对新结点的数据域和指针域（2个）进行初始化
  	New->data = KeyVal;
  	New->lchild = NULL;
  	New->rchild = NULL;
  
  	return New;
  }
  

  插入新节点

  向BST树中加入新节点，左子树的键值比根节点小，右子树的键值比根节点大，插入前需要注意判断树是否为空，且与根节点比较，递归比较，直到叶子节点

   /****************************************************************
    *
    *	name	 :	BSTree_InsertNode
    *	function :  创建一个新结点，并进行初始化
    *	argument :  @KeyVal：键值
    *             @Root：  根节点
    *	retval	 :  None
    *	author	 :  yq_dyx@163.com
    *	date	 :  2024/05/06
    * note	 :  None
    * 	
   ****************************************************************/
  //向BST树中加入节点   规则：根节点的左子树的键值都是比根节点小的，根节点的右子树的键值都是比根节点大的
  bool BSTree_InsertNode(BSTnode_t *Root,DataType_t KeyVal)
  {
  
  	//为了避免根节点地址丢失，所以需要对地址进行备份
  	BSTnode_t *Proot = Root;
  
  
  	//1.创建新节点并对新结点进行初始化
  	BSTnode_t * New = BSTree_NewNode(KeyVal);
  	if (NULL == New)
  	{
  		printf("Create NewNode Error\n");
  		return false;
  	}
  
  	//2.此时分析当前的BST树是否为空树，有2种情况（空树 or 非空树）
  	if (NULL == Root)
  	{
  		//此时BST树为空树，则直接把新节点作为BST树的根节点
  		Root = New;
  	}
  	else
  	{
  		while(Proot)
  		{
  			
  			//新节点的键值和根节点的键值进行比较,如果相等则终止函数
  			if (Proot->data == New->data)
  			{
  				printf("Can Not Insert,.....\n");
  				return false;
  			}
  			//新节点的键值和根节点的键值进行比较,如果不相等继续分析
  			else
  			{
  				//新节点的键值小于根节点的键值，则把根节点的左子树作为新的根
  				if( New->data < Proot->data )
  				{
  					if (Proot->lchild == NULL)
  					{
  						Proot->lchild = New;
  						break;
  					}
  
  					Proot = Proot->lchild;
  
  				}
  				else
  				{
  					if (Proot->rchild == NULL)
  					{
  						Proot->rchild = New;
  						break;
  					}
  
  					Proot = Proot->rchild;
  				}
  			}
  		}
  
  	}
  
  	return true;
  }
  

主函数测试

int main(int argc, char const *argv[])
{
	//1.创建一个带根节点的BST树
	BSTnode_t *root =  BSTree_Create(10);

	//2.向BST树中插入新节点
	BSTree_InsertNode(root,5);
	BSTree_InsertNode(root,20);
	BSTree_InsertNode(root,7);
	BSTree_InsertNode(root,12);
	BSTree_InsertNode(root,8);
	BSTree_InsertNode(root,3);
	BSTree_InsertNode(root,25);
	BSTree_InsertNode(root,11);

	draw(root);
	
	return 0;
}

已经经过测试验证并成功，测试结果如代码的测试结果一致，如图：

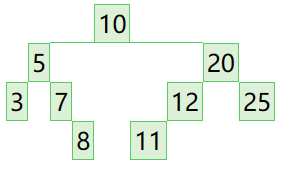
希望看完代码的你发现错误，请评论批评指正，非常感谢。并希望以上的代码能对同是初学者的你有所帮助，大家一起加油吧