数据结构之二叉树

二叉树定义

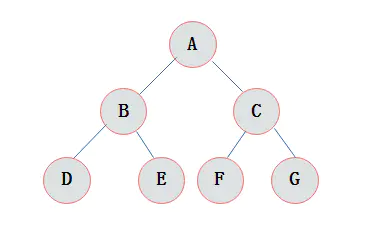
二叉树是n(n>=0)个结点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树组成。

二叉树特点

1）每个结点最多有两颗子树，所以二叉树中不存在度大于2的结点。
2）左子树和右子树是有顺序的，次序不能任意颠倒。
3）即使树中某结点只有一棵子树，也要区分它是左子树还是右子树。

二叉树性质

1）在二叉树的第i层上最多有2i-1 个节点 。（i>=1）
2）二叉树中如果深度为k,那么最多有2k-1个节点。(k>=1）
3）n0=n2+1 n0表示度数为0的节点数，n2表示度数为2的节点数。
4）在完全二叉树中，具有n个节点的完全二叉树的深度为[log2n]+1，其中[log2n]是向下取整。
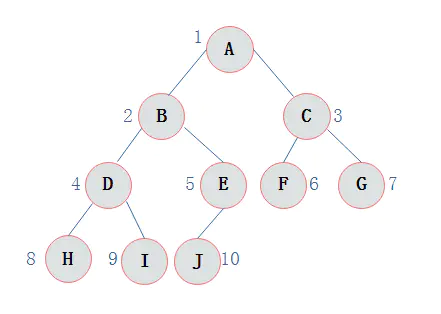
5）若对含 n 个结点的完全二叉树从上到下且从左至右进行 1 至 n 的编号，则对完全二叉树中任意一个编号为 i 的结点有如下特性：

(1) 若 i=1，则该结点是二叉树的根，无双亲, 否则，编号为 [i/2] 的结点为其双亲结点;
(2) 若 2i>n，则该结点无左孩子， 否则，编号为 2i 的结点为其左孩子结点；
(3) 若 2i+1>n，则该结点无右孩子结点， 否则，编号为2i+1 的结点为其右孩子结点。

满二叉树

满二叉树：在一棵二叉树中。如果所有分支结点都存在左子树和右子树，并且所有叶子都在同一层上，这样的二叉树称为满二叉树。
满二叉树的特点有：
1）叶子只能出现在最下一层。出现在其它层就不可能达成平衡。
2）非叶子结点的度一定是2。
3）在同样深度的二叉树中，满二叉树的结点个数最多，叶子数最多。

 

 

 

完全二叉树

完全二叉树：对一颗具有n个结点的二叉树按层编号，如果编号为i(1<=i<=n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同，则这棵二叉树称为完全二叉树。

 

特点：
1）叶子结点只能出现在最下层和次下层。
2）最下层的叶子结点集中在树的左部。
3）倒数第二层若存在叶子结点，一定在右部连续位置。
4）如果结点度为1，则该结点只有左孩子，即没有右子树。
5）同样结点数目的二叉树，完全二叉树深度最小。
注：满二叉树一定是完全二叉树，但反过来不一定成立。

 

二叉树的存储结构

顺序存储

 

对于右斜树极端情况，采用顺序存储的方式是十分浪费空间的。因此，顺序存储一般适用于完全二叉树

 

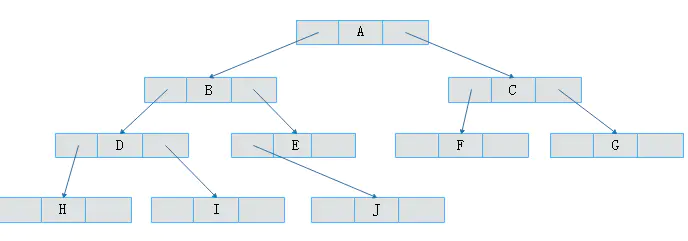
二叉链表

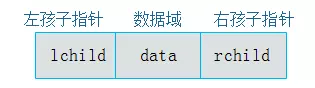
既然顺序存储不能满足二叉树的存储需求，那么考虑采用链式存储。由二叉树定义可知，二叉树的每个结点最多有两个孩子。因此，可以将结点数据结构定义为一个数据和两个指针域。

 

定义结点代码：

typedef struct BiTNode{
    TElemType data;//数据
    struct BiTNode *lchild, *rchild;//左右孩子指针
} BiTNode, *BiTree;

二叉树遍历

二叉树的访问次序可以分为四种：

前序遍历
中序遍历
后序遍历
层序遍历

递归实现代码如下：


/*二叉树的前序遍历递归算法*/
void PreOrderTraverse(BiTree T)
{
    if(T==NULL)
    return;
    printf("%c", T->data);  /*显示结点数据，可以更改为其他对结点操作*/
    PreOrderTraverse(T->lchild);    /*再先序遍历左子树*/
    PreOrderTraverse(T->rchild);    /*最后先序遍历右子树*/
}


/*二叉树的中序遍历递归算法*/
void InOrderTraverse(BiTree T)
{
    if(T==NULL)
    return;
    InOrderTraverse(T->lchild); /*中序遍历左子树*/
    printf("%c", T->data);  /*显示结点数据，可以更改为其他对结点操作*/
    InOrderTraverse(T->rchild); /*最后中序遍历右子树*/
}


/*二叉树的后序遍历递归算法*/
void PostOrderTraverse(BiTree T)
{
    if(T==NULL)
    return;
    PostOrderTraverse(T->lchild);   /*先后序遍历左子树*/
    PostOrderTraverse(T->rchild);   /*再后续遍历右子树*/
    printf("%c", T->data);  /*显示结点数据，可以更改为其他对结点操作*/
}