person reid评价指标——CMC原理及代码解析，mAP
CMC
CMC全程是Cumulative Matching Characteristics, 是行人重识别问题中的经典评价指标。该曲线的横坐标为rank，纵坐标为识别率百分比。rank n表示识别结果相似性降序排列中前n个结果包含目标。识别率是rank n 的数目#(rank n)占总的query样本数的比例。如下图
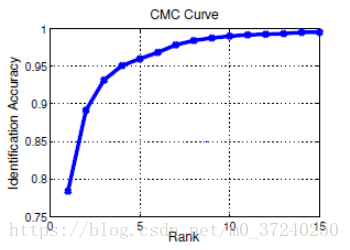
CMC曲线图来源 https://blog.csdn.net/m0_37240250/article/details/79942939
代码解释
先贴代码
代码来源 [港中文Xiaogang Wang教授 主页]
function C = cmc(D, varargin)
% CMC computes the Cumulative Match Characteristic.
% C = CMC(D) computes the CMC of given distance matrix D between each pair
% of gallery and probe person. Both gallery and probe persons are
% assumed to be unique, i.e., the i-th gallery person matches only to
% the i-th probe person. D(i, j) should be the distance between
% gallery instance i and probe instance j.
% 单个参数C = CMC(D)时表示gallery和probe中的identity都是独一无二的，
% 即gallery中第i个person只匹配probe set第i个person
%
% C = CMC(D, G, P) computes the CMC with G and P are id labels of each
% person in gallery and probe sets. D is M*N where M and N are the lengths of
% vector G and P, respectively. This function will first randomly select
% exactly one instance among for each gallery identity and then calculate
% the CMC of this sub-matrix. This procedure will be repeated 100 times
% and the final result is the mean of them.
% 三个参数C = CMC(D, G, P),G和P是gallery和probe中person的id label,
% 所以D的高=G的个数，D的宽=P的个数
% 该脚本先对galleray中的每个identity随机挑选一个instance(同一个identity可能有多个instance),
% 计算子矩阵的CMC,然后重复一百次,求均值
switch nargin
% nargin 针对当前正在执行的函数，返回函数调用中给定函数输入参数的数目
% nargin(fun) 返回 fun 函数定义中出现的输入参数的数目
% 如果该函数定义中包含 varargin，那么 nargin 返回输入数目的负数
% 例如，如果 myFun 函数声明输入 a、b 和 varargin，那么 nargin('myFun') 返回
% -3,就可以确定varargin前有2个参数
case 1
assert(ismatrix(D));
assert(size(D, 1) == size(D, 2));% 判断是矩阵且是方阵
case 3
G = varargin{1};
P = varargin{2};
assert(isvector(G));
assert(isvector(P));
assert(length(G) == size(D, 1));
assert(length(P) == size(D, 2));
otherwise
error('Invalid inputs');
end
if nargin == 1
C = cmc_core(D, 1:size(D, 1), 1:size(D, 1));
else
gtypes = union(G, []);%求集合，防止重复label
ngtypes = length(gtypes);
ntimes = 100;
C = zeros(ngtypes, ntimes);%宽是100，有100条曲线求均值
for t = 1:ntimes
subdist = zeros(ngtypes, size(D, 2));
for i = 1:ngtypes
j = find(G == gtypes(i));%寻找gtypes(i)相同的G中label
k = j(randi(length(j)));% j可能有多个值，从中随机选一个
subdist(i, :) = D(k, :);%选取D中对应的行向量（该Label到probe set中每个label的距离的向量）
end
C(:, t) = cmc_core(subdist, gtypes, P);
end
C = mean(C, 2);
end
end
function C = cmc_core(D, G, P)
m = size(D, 1);
n = size(D, 2);
[~, order] = sort(D);%二维矩阵时，对矩阵的每一列分别进行升序排序,即query中每个label在gallery中相似度的升序
match = (G(order) == repmat(P, [m, 1]));%(m*n==m*n),找矩阵中对应相同元素
%repmat(P, [m, 1])是以P为unit构建m(unit)X1(unit)的矩阵
% G(order)与order/D大小一致，即按照order里面每列的排序重新排列G
C = cumsum(sum(match, 2) / n);
%sum(match, 2)每行累加
%cumsum是将矩阵按列进行求和，每一项是前面之和（类似于积分曲线）
end
原理解释
脚本中单个参数CMC(D)是多参数的特殊形式，这里只解释多参数调用
对于函数调用CMC(D, G, P)，定义
- G为gallery中每个人的label向量，大小为Mx1
- P为probe sets(query)中每个person的label向量，大小为Nx1
- D是gallery和probe sets中两两person的特征距离矩阵，大小为MxN，
如下图所示
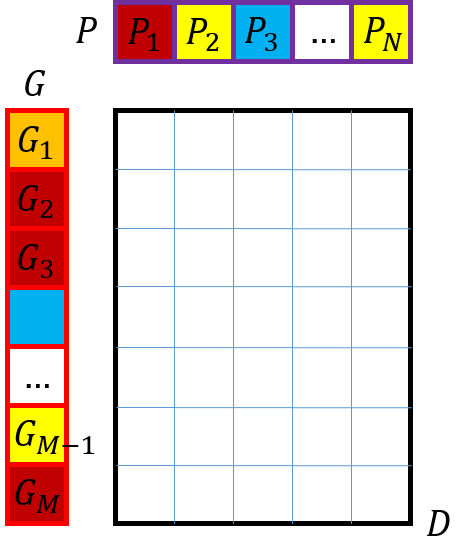
对G中的label求集合，得到G’，即向量中不出现重复的label；
G’中每个label对应的D中的行向量组成新的特征距离矩阵D’。其中，对于某些label在G中多次出现，随机选取其中的一个并抽取在D中的行向量。
如下图所示，G2,G3，GM随机选一个
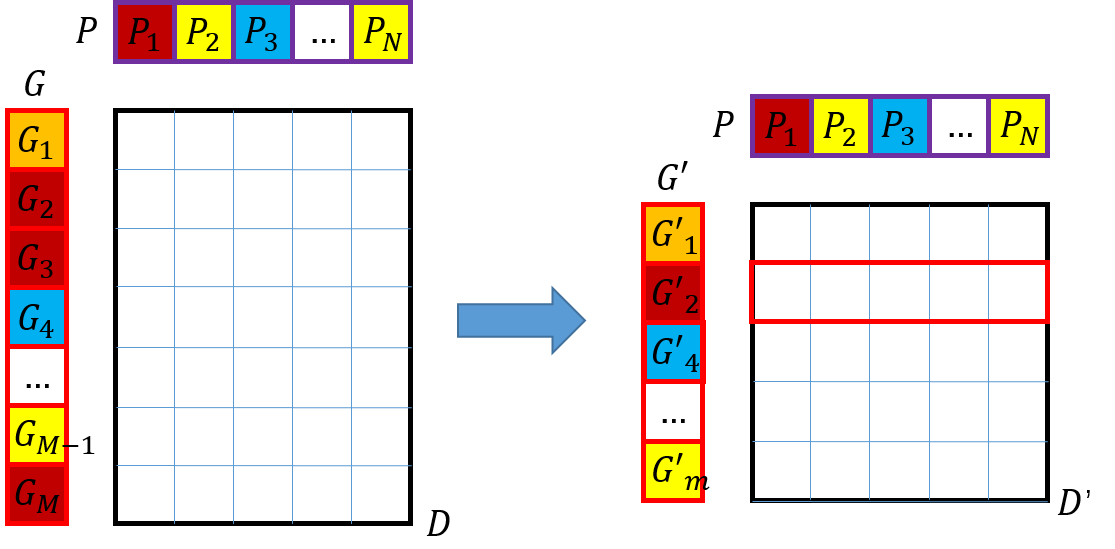
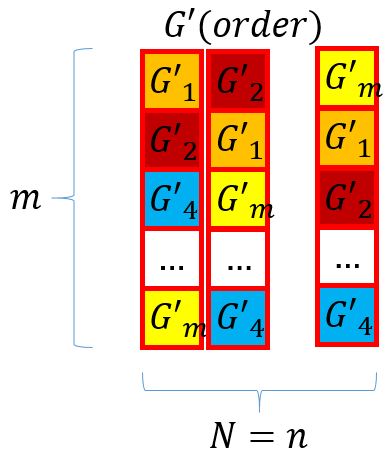
对D’按列进行升序排列，逐列记录下排列顺序的矩阵order，并按照每列的排列顺序重新排列G’（每一列重拍一次G’），得到label矩阵G’(order)。
order获取示例（以一列向量为例）：
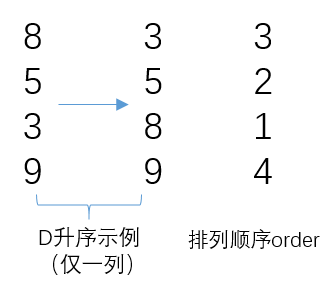
G’(order)如下：
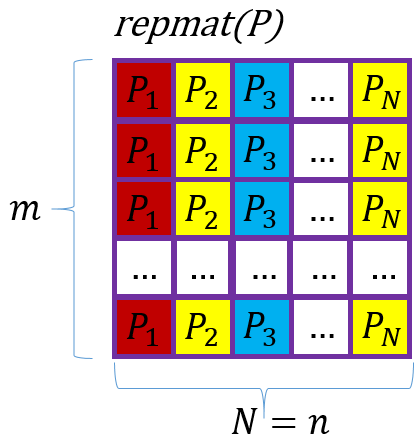
以P为单元复制[m,1]次，得到repmat(P)矩阵
求和G’(order)矩阵中相等的元素的位置，
match = (G(order) == repmat(P, [m, 1]))
得到0/1二值矩阵match，大小为m*n，其中1为该位置处两个矩阵对应元素相等，0为不等
求CMC分数：
C = cumsum(sum(match, 2) / n)
sum(match, 2) / n是对match矩阵按行求均值(m*1)，cumsum()是逐列求积分(m*1)。
cunsum示例
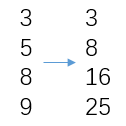
这样就得到了一条CMC中的rank曲线，重复100次求均值即输出。
mAP
Precision & Recall
一般来说，Precision就是检索出来的条目（比如：文档、网页等）有多少是准确的，Recall就是所有准确的条目有多少被检索出来了。
正确率 = 提取出的正确信息条数 / 提取出的信息条数
召回率 = 提取出的正确信息条数 / 样本中的信息条数
准确率和召回率都是针对同一类别来说的，并且只有当检索到当前类别时才进行计算（因为P-R曲线，只在recall的点算，而recall只在TP点算），比如在person re-id中，一个人的label为m1，在测试集中包含3张此人的图像，检索出来的图像按照得分从高到低顺序为m1、m2、m1、m3、m4、m1….，此时
第一次检索到m1，提取出的正确信息条数=1，提取出的信息条数=1，样本中的信息条数=3，正确率=1/1=100%，召回率=1/3=33.33%；
第二次检索到m1，提取出的正确信息条数=2，提取出的信息条数=3，样本中的信息条数=3，正确率=2/3=66.66%，召回率=2/3=66.66%；
第三次检索到m1，提取出的正确信息条数=3，提取出的信息条数=6，样本中的信息条数=3，正确率=3/6=50%，召回率=3/3=100%；
平均正确率AP=（100%+66.66%+50%）/3=72.22%
对Precision求Mean Average等同于求P-R曲线下的面积（积分）
mAP
而当需要检索的不止一个人时，此时正确率则取所有人的平均mAP。
--转载自CSDN
