最小生成树（MST）Prim算法和Kruskal算法

刚学完最小生成树，赶紧写写学习的心得（其实是怕我自己忘了）

最小生成树概念:一个有 n 个结点的连通图的生成树是原图的极小连通子图，且包含原图中的所有 n 个结点，并且有保持图连通的最少的边。

就是说如果我们想把一张有n个点的图连接起来，那我们就只需要n-1条边（原因显然：就如同一条有n个点的线段，他们之间最少需要n-1条边连起来）

最小生成树就是寻找值最小的这n-1个点，把他们加和。

首先，最小生成树最基本的算法是Prim和Kruskal算法

Prim算法：

算法分析&思想讲解：
Prim算法采用“蓝白点”思想：白点代表已经进入最小生成树的点，蓝点代表未进入最小生成树的点。
Prim算法每次循环都将一个蓝点u变为白点，并且此蓝点u与白点相连的最小边权min[u]还是当前所有蓝点中最小的。

这样相当于向生成树中添加了n-1次最小的边，最后得到的一定是最小生成树。

                                                                

    

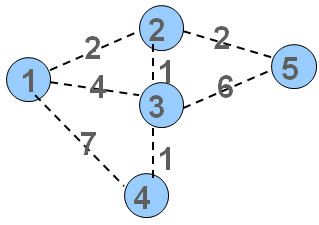
Prim算法的好处就在于它与边无关，主要用于稠密图，复杂度为O（n^2），实用度不如Kruskal算法高

代码介绍：（好像不可以直接用，有点问题）

#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
const int MAXN=5010;
int t[MAXN][MAXN];
bool b[MAXN];
int MIN[MAXN];
int main(){
     memset(b,false,sizeof(b));
     memset(t,127,sizeof(t));
     memset(MIN,127,sizeof(MIN));                //把每一条未赋值的边赋为较大的一个数
    int n,m; 
    int ans=0;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)t[i][i]=0;
    for(int i=1;i<=n;i++){               //邻接矩阵存图 
       for (int j=1;j<=n;j++){           //不同问题存图方式不同 
              cin>>t[i][j];
       }
    }
    MIN[1]=0;
 //先找点： 
    for(int i=1;i<=n;i++){
        int x=0;                        //x为0 就是说一开始是从一个虚拟点开始的 然后我们找与它相邻的边并且还没被找过的点 
         for(int j=1;j<=n;j++){         
            if(!b[j]&&MIN[j]<MIN[x]){  //我们以这一个点开始寻找与它相邻的最小的边 
                x=j;                   //然后就标记这个点以便于接着用这个点继续往下找 
            }
        }
    
         b[x]=true;                 //找完这个点后就变成白点，表示已找过 
    //再扩边： 
         for(int j=1;j<=n;j++){          
             if(!b[j]&&MIN[j]>t[x][j]){   //这段代码就是给我们刚找到的X点的邻边赋实际值，这样在下次寻找X的最小边时就可以找到啦 
                 MIN[j]=t[x][j];           //所以说找点的代码就比较好理解了 
            }
        }
    }
   for(int i=1;i<=n;i++){
       ans+=MIN[i];//求最小和 
   }
    cout<<ans<<endl; 
    return 0;
}

知识扩展：本算法在移动通信、智能交通、移动物流、生产调度等物联网相关领域都有十分现实的意义，采用好的算法，就能节省成本提高效率。

 

 

Kruskal算法：

算法分析：

Kruskal算法是将一个连通块当做一个集合。Kruskal首先将所有的边按从小到大顺序排序（一般使用快排），并认为每一个点都是孤立的，分属于n个独立的集合。

然后按顺序枚举每一条边。如果这条边连接着两个不同的集合，那么就把这条边加入最小生成树，这两个不同的集合就合并成了一个集合（这就是一条边）；

如果这条边连接的两个点属于同一集合（说明这条边找过了），就跳过。直到选取了n-1条边为止。

思路讲解：

Kruskal算法每次都选择一条最小的，且能合并两个不同集合的边，一张n个点的图总共选取n-1次边。因为每次我们选的都是最小的边，所以最后的生成树一定是最小生成树。每次我们选的边都能够合并两个集合，最后n个点一定会合并成一个集合。通过这样的贪心策略，Kruskal算法就能得到一棵有n-1条边，连接着n个点的最小生成树。
　　
Kruskal算法的时间复杂度为O(E*logE)，E为边数。

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int MAXN=10010;
int fa[MAXN];

int m,k,ans,x;
struct Edge{
    int s,t,w;
}edge[MAXN<<1];
int find(int x){
    if(fa[x]==x)return x;
    return fa[x]=find(fa[x]);
}
void unionn(int x,int y){
    int xx=find(x);
    int yy=find(y);
    if(xx!=yy){
        fa[xx]=yy;
    }
} 
int cmp(const Edge &a,const Edge &b){
    if(a.w<b.w)return 1;
    else return 0;
}
int main(){
    int n;
    cin>>n; 
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
        cin>>x;
        if(x!=0){
            m++;
            edge[m].s=i;
            edge[m].t=j;
            edge[m].w=x;
            }    
        }
    }
    for(int i=1;i<=n;i++)fa[i]=i;
    sort(edge+1,edge+1+m,cmp);//按照权值大小排序 
    for(int i=1;i<=m;i++){
        if(find(edge[i].s)!=find(edge[i].t)){//查询两条边是否在一个集合里 
            unionn(edge[i].s,edge[i].t);//因为是按最小值排序，我们所能选择的肯定是最小的 
            ans+=edge[i].w;//然后加和 
            k++;//计边的数 
        }
        if(k==n-1)break;//如果搜够了n-1条边就停止 
    }
    cout<<ans<<endl;
return 0;    
} 

 

 End...