《python数据分析基础》之描述性统计与建模
1、数据集
红葡萄酒数据集:
http://archive.ics.uci.edu/ml/machine-learning-databases/wine-quality/winequality-red.csv
白葡萄酒数据集:
http://archive.ics.uci.edu/ml/machine-learning-databases/wine-quality/winequality-white.csv
红葡萄酒文件中包含1599条观测,白葡萄酒文件包含4898条观测。输入变量是葡萄酒的物理化学成分和特性,包括非挥发性酸、挥发性酸、柠檬酸、残余糖分、氯化物、游离二氧化硫、总二氧化硫、密度、pH值、硫酸盐和酒精含量。我们将两个文件合并,并增加一列type变量,用于区分白葡萄酒和红葡萄酒:
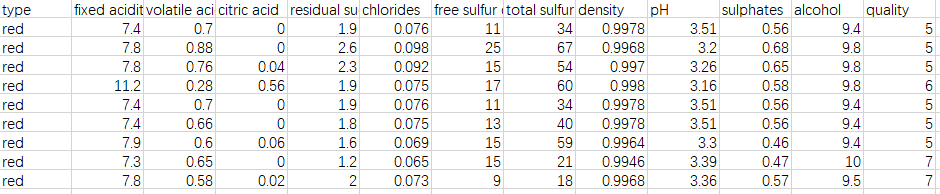
2、描述性统计
#!/usr/bin/env python3 import pandas as pd # 将数据集读入到pandas数据框中,分隔符为逗号 f = open('F://python入门//数据1//红葡萄酒和白葡萄酒//winequality-whole.csv') #read_csv读取时会自动识别表头,数据有表头时不能设置header为空(默认读取第一行,即header=0); #数据无表头时,若不设置header,第一行数据会被视为表头,应传入names参数设置表头名称或设置header=None。 wine = pd.read_csv(f, sep=',', header=0) #将标题行中的空格替换成下划线 wine.columns = wine.columns.str.replace(' ', '_') #使用head函数检查一下标题行和前五行数据 print('查看前五行数据:\n',wine.head()) # 显示所有变量的描述性统计量,这些统计量包括:总数、均值、标准差、最小值、第25个百分位数、 #中位数、第75个百分位数和最大值 #标准差是一组数据平均值分散程度的一种度量。一个较大的标准差,代表大部分数值和其平均值之间差异较大。 print('描述性统计:\n',wine.describe()) #找出唯一值,即quality列中删除重复值留下的数值 print('quality列去重后的值,从小到大输出:\n',sorted(wine.quality.unique())) # 计算值的频率 print('每个唯一值在数据集中出现的次数:\n',wine.quality.value_counts())
结果:
查看前五行数据: type fixed_acidity volatile_acidity ... sulphates alcohol quality 0 red 7.4 0.70 ... 0.56 9.4 5 1 red 7.8 0.88 ... 0.68 9.8 5 2 red 7.8 0.76 ... 0.65 9.8 5 3 red 11.2 0.28 ... 0.58 9.8 6 4 red 7.4 0.70 ... 0.56 9.4 5 [5 rows x 13 columns] 描述性统计: fixed_acidity volatile_acidity ... alcohol quality count 6497.000000 6497.000000 ... 6497.000000 6497.000000 mean 7.215307 0.339666 ... 10.491801 5.818378 std 1.296434 0.164636 ... 1.192712 0.873255 min 3.800000 0.080000 ... 8.000000 3.000000 25% 6.400000 0.230000 ... 9.500000 5.000000 50% 7.000000 0.290000 ... 10.300000 6.000000 75% 7.700000 0.400000 ... 11.300000 6.000000 max 15.900000 1.580000 ... 14.900000 9.000000 [8 rows x 12 columns] quality列去重后的值,从小到大输出: [3, 4, 5, 6, 7, 8, 9] 每个唯一值在数据集中出现的次数: 6 2836 5 2138 7 1079 4 216 8 193 3 30 9 5 Name: quality, dtype: int64
3、分组、直方图和t检验
#!/usr/bin/env python3 import pandas as pd import seaborn as sns import matplotlib.pyplot as plt import statsmodels.api as sm # 将数据集读入到pandas数据框中,分隔符为逗号 f = open('F://python入门//数据1//红葡萄酒和白葡萄酒//winequality-whole.csv') #read_csv读取时会自动识别表头,数据有表头时不能设置header为空(默认读取第一行,即header=0); #数据无表头时,若不设置header,第一行数据会被视为表头,应传入names参数设置表头名称或设置header=None。 wine = pd.read_csv(f, sep=',', header=0) #将标题行中的空格替换成下划线 wine.columns = wine.columns.str.replace(' ', '_') #按照葡萄酒类型显示质量的描述性统计量,分别打印红葡萄酒和白葡萄酒的摘要统计量 print('分别打印红葡萄酒和白葡萄酒的摘要统计量:\n',wine.groupby('type')[['quality']].describe()) #unstack函数将结果重新排列,使统计量显示在并排的两列中 print('分别打印红葡萄酒和白葡萄酒的摘要统计量(结果重排列):\n',wine.groupby('type')[['quality']].describe().unstack('type')) #按照葡萄酒类型显示质量的特定分位数值,quantile函数对质量列计算第25百分位数和第75百分位数 print('分别计算第25百分位数和第75百分位数(结果重排列):\n',wine.groupby('type')[['quality']].quantile([0.25, 0.75]).unstack('type')) #按照葡萄酒类型查看质量分布 red_wine = wine.loc[wine['type'] == 'red', 'quality'] white_wine = wine.loc[wine['type'] == 'white', 'quality'] #画布背景色为暗色 sns.set_style("dark") #该图显示密度分布,画直方图,直方图颜色为红色 sns.distplot(red_wine, norm_hist=True, kde=False, color="red", label="Red wine") sns.distplot(white_wine, norm_hist=True, kde=False, color="white", label="White wine") #设置x轴、y轴标签 sns.utils.axlabel("Quality Score", "Density") #设置图标题 plt.title("Distribution of Quality by Wine Type") #给图像加上图例 plt.legend() #图像显示 plt.show() #检验红葡萄酒和白葡萄酒的平均质量是否有所不同,分组计算标准差 print('分组计算标准差:\n',wine.groupby(['type'])[['quality']].agg(['std'])) #t检验统计量为tstat,p值为pvalue, #t检验主要用于样本含量较小或两样本总体方差相等,总体标准差σ未知的正态分布。df为自由度 #T检验是用t分布理论来推论差异发生的概率,从而比较两个平均数的差异是否显著。 #P越小,越有理由说明两者有差异,求出的p值如果小于5%,则拒绝原建设,即拒绝两样本均值不相等的假设 tstat, pvalue, df = sm.stats.ttest_ind(red_wine, white_wine) print('t统计量为: %.3f;p值为: %.4f;自由度为:%.1f;' % (tstat, pvalue,df))
结果:
分别打印红葡萄酒和白葡萄酒的摘要统计量: quality count mean std min 25% 50% 75% max type red 1599.0 5.636023 0.807569 3.0 5.0 6.0 6.0 8.0 white 4898.0 5.877909 0.885639 3.0 5.0 6.0 6.0 9.0 分别打印红葡萄酒和白葡萄酒的摘要统计量(结果重排列): type quality count red 1599.000000 white 4898.000000 mean red 5.636023 white 5.877909 std red 0.807569 white 0.885639 min red 3.000000 white 3.000000 25% red 5.000000 white 5.000000 50% red 6.000000 white 6.000000 75% red 6.000000 white 6.000000 max red 8.000000 white 9.000000 dtype: float64 分别计算第25百分位数和第75百分位数(结果重排列): quality type red white 0.25 5.0 5.0 0.75 6.0 6.0
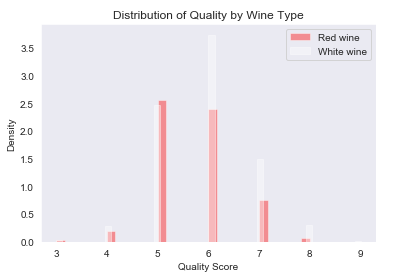
分组计算标准差: quality std type red 0.807569 white 0.885639 t统计量为: -9.686;p值为: 0.0000;自由度为:6495.0;
说明:该例使用t检验,判断红葡萄酒和白葡萄酒的平均评分是否有区别,结论是p<0.05,我们认为没有区别。t值为负代表前面一组样本的均值低于后面一组的均值,说明在统计意义上,白葡萄酒的平均质量评分大于红葡萄酒的平均质量评分。
4、成对变量之间的关系和相关性
#!/usr/bin/env python3 import numpy as np import pandas as pd import seaborn as sns import matplotlib.pyplot as plt # 将数据集读入到pandas数据框中,分隔符为逗号 f = open('F://python入门//数据1//红葡萄酒和白葡萄酒//winequality-whole.csv') #read_csv读取时会自动识别表头,数据有表头时不能设置header为空(默认读取第一行,即header=0); #数据无表头时,若不设置header,第一行数据会被视为表头,应传入names参数设置表头名称或设置header=None。 wine = pd.read_csv(f, sep=',', header=0) #将标题行中的空格替换成下划线 wine.columns = wine.columns.str.replace(' ', '_') # 计算所有变量两两之间的相关性矩阵 print('所有变量两两之间的相关性矩阵:\n',wine.corr()) # 从红葡萄酒和白葡萄酒的数据中取出一个“小”样本来进行绘图,抽取在统计图中使用的样本点 #np.random.choice是从data_frame中随机选择200个,replace代表的意思是抽样之后还放不放回去, #如果是False的话,那么出来的三个数都不一样,如果是True的话,有可能会出现重复的,因为前面的抽的放回去了。 def take_sample(data_frame, replace=False, n=200): return data_frame.loc[np.random.choice(data_frame.index, replace=replace, size=n)] #从红酒数据集中抽取200个样本 reds_sample = take_sample(wine.loc[wine['type'] == 'red', :]) #从白酒数据集中抽取200个样本 whites_sample = take_sample(wine.loc[wine['type'] == 'white', :]) #将400个样本放在一起组成新样本集 wine_sample = pd.concat([reds_sample, whites_sample]) #对总的数据集添加一列'in_sample',填充依据是此行的索引值是否在抽样数据的索引值中,如果在则置为1,否则置为0 wine['in_sample'] = np.where(wine.index.isin(wine_sample.index), 1., 0.) #crosstab交叉列表取值,第一个参数是列, 第二个参数是行. 还可以添加第三个参数,类似Excel中的透视表功能 print('样本与总数据集的统计:\n',pd.crosstab(wine.in_sample, wine.type, margins=True)) #seaborn的pairplot函数可以创建一个统计图矩阵,主对角线上的图以直方图或密度图的形式显示了每个变量的单变量分布。 #对角线之外的图以散点图的形式显示了每两个变量之间的双变量分布,散点图中可以有回归直线,也可以没有 #设置背景色为暗色 sns.set_style("dark") #第一个参数是完整数据集wine_sample,kind为可选图样,kind="reg"为使用回归,hue : 使用指定变量为分类变量画图 #diag_kind='hist'对角子图的图样,柱状图,palette使用调色板,markers点使用不同的形状, #vars要使用的数据中的变量 g = sns.pairplot(wine_sample, kind='reg', plot_kws={"ci": False, "x_jitter": 0.25, "y_jitter": 0.25}, hue='type', diag_kind='hist', diag_kws={"bins": 10, "alpha": 1.0}, palette=dict(red="red", white="white"), markers=["o", "s"], vars=['quality', 'alcohol', 'residual_sugar']) #添加标题,fontsize=14字体大小,horizontalalignment='center'文字居中,verticalalignment='top'顶部对齐 plt.suptitle('Histograms and Scatter Plots of Quality, Alcohol, and Residual Sugar', fontsize=14, horizontalalignment='center', verticalalignment='top', x=0.5, y=0.999) #显示图像 plt.show()
结果:
所有变量两两之间的相关性矩阵: fixed_acidity ... quality fixed_acidity 1.000000 ... -0.076743 volatile_acidity 0.219008 ... -0.265699 citric_acid 0.324436 ... 0.085532 residual_sugar -0.111981 ... -0.036980 chlorides 0.298195 ... -0.200666 free_sulfur_dioxide -0.282735 ... 0.055463 total_sulfur_dioxide -0.329054 ... -0.041385 density 0.458910 ... -0.305858 pH -0.252700 ... 0.019506 sulphates 0.299568 ... 0.038485 alcohol -0.095452 ... 0.444319 quality -0.076743 ... 1.000000 [12 rows x 12 columns] 样本与总数据集的统计: type red white All in_sample 0.0 1399 4698 6097 1.0 200 200 400 All 1599 4898 6497
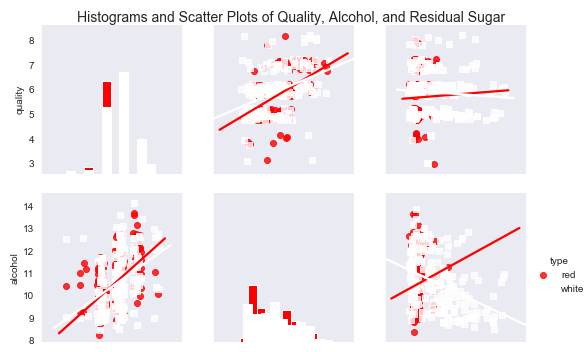
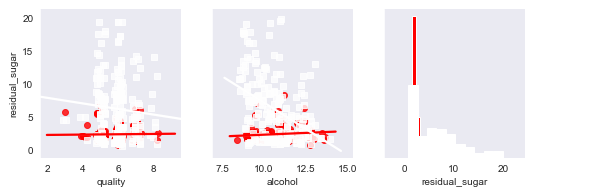
说明:
根据相关系数的符号,从输出中可以知道酒精含量、硫酸盐、pH值、游离二氧化硫和柠檬酸这些指标与质量是正相关的,相反,非挥发性酸、挥发性酸、残余糖分、氯化物、总二氧化硫和密度这些指标与质量是负相关的。
从统计图中可以看出,对于红葡萄酒和白葡萄酒来说,酒精含量的均值和标准差是大致相同的,但是,白葡萄酒残余糖分的均值和标准差却大于红葡萄酒残余糖分的均值和标准差。从回归直线可以看出,对于两种类型的葡萄酒,酒精含量增加时,质量评分也随之提高,相反,残余糖分增加时,白葡萄酒质量评分则随之降低。
5、使用最小二乘法估计进行线性回归
#!/usr/bin/env python3 import pandas as pd #import statsmodels.api as sm from statsmodels.formula.api import ols, glm # 将数据集读入到pandas数据框中,分隔符为逗号 f = open('F://python入门//数据1//红葡萄酒和白葡萄酒//winequality-whole.csv') #read_csv读取时会自动识别表头,数据有表头时不能设置header为空(默认读取第一行,即header=0); #数据无表头时,若不设置header,第一行数据会被视为表头,应传入names参数设置表头名称或设置header=None。 wine = pd.read_csv(f, sep=',', header=0) #将标题行中的空格替换成下划线 wine.columns = wine.columns.str.replace(' ', '_') #将一个字符串赋给变量my_formula,~左侧的变量quality是因变量,波浪线右侧的变量是自变量 my_formula = 'quality ~ alcohol + chlorides + citric_acid + density +fixed_acidity + free_sulfur_dioxide + pH' \ '+ residual_sugar + sulphates + total_sulfur_dioxide + volatile_acidity' #使用公式和数据拟合一个普通最小二乘法模型,并将结果赋值给lm lm = ols(my_formula, data=wine).fit() # 或者,也可以使用广义线性模型(glm)语法进行线性回归 #lm = glm(my_formula, data=wine, family=sm.families.Gaussian()).fit() #打印结果的摘要信息,包含了模型系数,系数的标准差,修正R^2,F统计量等信息 print('摘要:\n',lm.summary()) print('………………') #打印出一个列表,包含模型对象lm的所有信息 print("打印出一个列表,包含模型对象lm的所有信息:\n%s" % dir(lm)) #打印模型的系数 print("模型的系数:\n%s" % lm.params) #系数的标准差 print("模型系数的标准差:\n%s" % lm.bse) #修正的R^2 print("修正的R^2:%.2f" % lm.rsquared_adj) #F统计量和它的P值 print("F统计量: %.1f,和它的P值: %.2f" % (lm.fvalue, lm.f_pvalue)) #模型的拟合值 print("观测总数: %d,拟合值的数量: %d" % (lm.nobs, len(lm.fittedvalues)))
结果:
摘要: OLS Regression Results ============================================================================== Dep. Variable: quality R-squared: 0.292 Model: OLS Adj. R-squared: 0.291 Method: Least Squares F-statistic: 243.3 Date: Sat, 18 Apr 2020 Prob (F-statistic): 0.00 Time: 23:01:26 Log-Likelihood: -7215.5 No. Observations: 6497 AIC: 1.445e+04 Df Residuals: 6485 BIC: 1.454e+04 Df Model: 11 Covariance Type: nonrobust ======================================================================================== coef std err t P>|t| [0.025 0.975] ---------------------------------------------------------------------------------------- Intercept 55.7627 11.894 4.688 0.000 32.447 79.079 alcohol 0.2670 0.017 15.963 0.000 0.234 0.300 chlorides -0.4837 0.333 -1.454 0.146 -1.136 0.168 citric_acid -0.1097 0.080 -1.377 0.168 -0.266 0.046 density -54.9669 12.137 -4.529 0.000 -78.760 -31.173 fixed_acidity 0.0677 0.016 4.346 0.000 0.037 0.098 free_sulfur_dioxide 0.0060 0.001 7.948 0.000 0.004 0.007 pH 0.4393 0.090 4.861 0.000 0.262 0.616 residual_sugar 0.0436 0.005 8.449 0.000 0.033 0.054 sulphates 0.7683 0.076 10.092 0.000 0.619 0.917 total_sulfur_dioxide -0.0025 0.000 -8.969 0.000 -0.003 -0.002 volatile_acidity -1.3279 0.077 -17.162 0.000 -1.480 -1.176 ============================================================================== Omnibus: 144.075 Durbin-Watson: 1.646 Prob(Omnibus): 0.000 Jarque-Bera (JB): 324.712 Skew: -0.006 Prob(JB): 3.09e-71 Kurtosis: 4.095 Cond. No. 2.49e+05 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. [2] The condition number is large, 2.49e+05. This might indicate that there are strong multicollinearity or other numerical problems. ……………… 打印出一个列表,包含模型对象lm的所有信息: ['HC0_se', 'HC1_se', 'HC2_se', 'HC3_se', '_HCCM', '__class__', '__delattr__', '__dict__', '__dir__', '__doc__', '__eq__', '__format__', '__ge__', '__getattribute__', '__gt__', '__hash__', '__init__', '__init_subclass__', '__le__', '__lt__', '__module__', '__ne__', '__new__', '__reduce__', '__reduce_ex__', '__repr__', '__setattr__', '__sizeof__', '__str__', '__subclasshook__', '__weakref__', '_cache', '_data_attr', '_get_robustcov_results', '_is_nested', '_wexog_singular_values', 'aic', 'bic', 'bse', 'centered_tss', 'compare_f_test', 'compare_lm_test', 'compare_lr_test', 'condition_number', 'conf_int', 'conf_int_el', 'cov_HC0', 'cov_HC1', 'cov_HC2', 'cov_HC3', 'cov_kwds', 'cov_params', 'cov_type', 'df_model', 'df_resid', 'diagn', 'eigenvals', 'el_test', 'ess', 'f_pvalue', 'f_test', 'fittedvalues', 'fvalue', 'get_influence', 'get_prediction', 'get_robustcov_results', 'initialize', 'k_constant', 'llf', 'load', 'model', 'mse_model', 'mse_resid', 'mse_total', 'nobs', 'normalized_cov_params', 'outlier_test', 'params', 'predict', 'pvalues', 'remove_data', 'resid', 'resid_pearson', 'rsquared', 'rsquared_adj', 'save', 'scale', 'ssr', 'summary', 'summary2', 't_test', 't_test_pairwise', 'tvalues', 'uncentered_tss', 'use_t', 'wald_test', 'wald_test_terms', 'wresid'] 模型的系数: Intercept 55.762750 alcohol 0.267030 chlorides -0.483714 citric_acid -0.109657 density -54.966942 fixed_acidity 0.067684 free_sulfur_dioxide 0.005970 pH 0.439296 residual_sugar 0.043559 sulphates 0.768252 total_sulfur_dioxide -0.002481 volatile_acidity -1.327892 dtype: float64 模型系数的标准差: Intercept 11.893899 alcohol 0.016728 chlorides 0.332683 citric_acid 0.079619 density 12.137473 fixed_acidity 0.015573 free_sulfur_dioxide 0.000751 pH 0.090371 residual_sugar 0.005156 sulphates 0.076123 total_sulfur_dioxide 0.000277 volatile_acidity 0.077373 dtype: float64 修正的R^2:0.29 F统计量: 243.3,和它的P值: 0.00 观测总数: 6497,拟合值的数量: 6497
说明,这里就最小二乘法的拟合结果做一个结果分析,R是相关系数,R^2是相关系数的平方,又称判定系数,判定线性回归的拟合程度,用来说明用自变量解释因变量变异的程度(所占比例)。调整后的判定系数,用来估计标准误差,R^2衡量方程拟合优度,R^2越大越好,一般的,大于0.8说明方程对样本点的拟合效果很好,0.5~0.8之间也可以接受,时间序列的话,R^2很容易达到很大,如果是截面数据,R^2要求没那么严格,但要注意的是,R^2统计量不是检验的统计量,只衡量显著性。F值(F-statistic)为243.3,显著性概率(Prob (F-statistic))为0.00,表明回归极显著。F是检验方程显著性的统计量,是平均的回归平方和与平均剩余平方和之比,越大越好。前面提到的t统计量对应的概率值(tstat, pvalue, df)中pvalue的值为0.0000,要求小于给定的显著性水平(一般是0.05,0.01等),pvalue越接近0越好,如果0.01<pvalue<0.05,则为差异显著,如果pvalue<0.01,则为差异极显著。
拟合方程:
y=55.762750+0.267030x1-0.483714x2-0.109657x3-54.966942x4+0.067684x5+0.005970x6+0.439296x7+0.043559x8+0.768252x9-0.002481x10-1.327892x11
Intercept为截距项。截距系数没有具体意义。
模型自变量系数的意义:在其他自变量保持不变的情况下,这个自变量发生1个单位的变化时,导致葡萄酒质量评分发生的平均变化。例如,酒精含量系数的含义就是,从平均意义上来说,如果两种葡萄酒其他自变量的值都相同,那么酒精含量高一个单位的葡萄酒的质量评分就要比另一种葡萄酒的质量评分高出0.27分。
6、自变量标准化
#!/usr/bin/env python3 import pandas as pd from statsmodels.formula.api import ols, glm # 将数据集读入到pandas数据框中,分隔符为逗号 f = open('F://python入门//数据1//红葡萄酒和白葡萄酒//winequality-whole.csv') #read_csv读取时会自动识别表头,数据有表头时不能设置header为空(默认读取第一行,即header=0); #数据无表头时,若不设置header,第一行数据会被视为表头,应传入names参数设置表头名称或设置header=None。 wine = pd.read_csv(f, sep=',', header=0) #将标题行中的空格替换成下划线 wine.columns = wine.columns.str.replace(' ', '_') #将一个字符串赋给变量my_formula,~左侧的变量quality是因变量,波浪线右侧的变量是自变量 my_formula = 'quality ~ alcohol + chlorides + citric_acid + density +fixed_acidity + free_sulfur_dioxide + pH' \ '+ residual_sugar + sulphates + total_sulfur_dioxide + volatile_acidity' # 创建一个名为dependent_variable的序列来保存质量数据 dependent_variable = wine['quality'] # 创建一个名为independent_variables的数据框来保存初始的葡萄酒数据集中除quality、type和in_sample之外的所有变量 #s.difference(t)返回在集合s中但不在t中的元素 independent_variables = wine[wine.columns.difference(['quality', 'type', 'in_sample'])] # 对自变量进行标准化 # 对每个变量,在每个观测中减去变量的均值 # 并且使用结果除以变量的标准差(最大值-最小值) independent_variables_standardized = (independent_variables - independent_variables.mean()) / independent_variables.std() # 将因变量quality作为一列添加到自变量数据框中 # 创建一个带有标准化自变量的新数据集,当axis=1时,是在行上进行操作 wine_standardized = pd.concat([dependent_variable, independent_variables_standardized], axis=1) # 重新进行线性回归,并查看一下摘要统计 lm_standardized = ols(my_formula, data=wine_standardized).fit() #查看摘要统计信息 print(lm_standardized.summary())
结果:
OLS Regression Results ============================================================================== Dep. Variable: quality R-squared: 0.292 Model: OLS Adj. R-squared: 0.291 Method: Least Squares F-statistic: 243.3 Date: Sun, 19 Apr 2020 Prob (F-statistic): 0.00 Time: 11:04:39 Log-Likelihood: -7215.5 No. Observations: 6497 AIC: 1.445e+04 Df Residuals: 6485 BIC: 1.454e+04 Df Model: 11 Covariance Type: nonrobust ======================================================================================== coef std err t P>|t| [0.025 0.975] ---------------------------------------------------------------------------------------- Intercept 5.8184 0.009 637.785 0.000 5.800 5.836 alcohol 0.3185 0.020 15.963 0.000 0.279 0.358 chlorides -0.0169 0.012 -1.454 0.146 -0.040 0.006 citric_acid -0.0159 0.012 -1.377 0.168 -0.039 0.007 density -0.1648 0.036 -4.529 0.000 -0.236 -0.093 fixed_acidity 0.0877 0.020 4.346 0.000 0.048 0.127 free_sulfur_dioxide 0.1060 0.013 7.948 0.000 0.080 0.132 pH 0.0706 0.015 4.861 0.000 0.042 0.099 residual_sugar 0.2072 0.025 8.449 0.000 0.159 0.255 sulphates 0.1143 0.011 10.092 0.000 0.092 0.137 total_sulfur_dioxide -0.1402 0.016 -8.969 0.000 -0.171 -0.110 volatile_acidity -0.2186 0.013 -17.162 0.000 -0.244 -0.194 ============================================================================== Omnibus: 144.075 Durbin-Watson: 1.646 Prob(Omnibus): 0.000 Jarque-Bera (JB): 324.712 Skew: -0.006 Prob(JB): 3.09e-71 Kurtosis: 4.095 Cond. No. 9.61 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
说明,关于这个模型,普通最小二乘回归是通过使残差平方和最小化来估计未知的β参数值的,这里的残差是指自变量观测值与拟合值之间的差别。因为残差大小是依赖于自变量的测量单位的,所以如果自变量的测量单位相差很大的话,那么将自变量标准化后,就可以更容易对模型进行解释了。对自变量进行标准化的方法是,先从自变量的每个观测值中减去均值,然后再除以这个自变量的标准差。自变量标准化完成以后,它的均值为0,标准差为1。
自变量标准化会改变对模型系数的解释。现在每个自变量系数的含义是,不同的葡萄酒在其他自变量均相同的情况下,某个自变量相差1个标准差,会使葡萄酒的质量评分平均相差多少个标准差。举个例子,酒精含量的系数意义是,从平均意义上说,如果两种葡萄酒其他自变量的值都相同,那么酒精含量高1个标准差的葡萄酒的质量评分就要比另一种葡萄酒的质量评分高出0.32个标准差。自变量标准化同样会改变对截距的解释。当解释变量被标准化后,截距表示的就是当所有自变量取值为均值时因变量的均值。
7、预测
#!/usr/bin/env python3 import pandas as pd from statsmodels.formula.api import ols, glm # 将数据集读入到pandas数据框中,分隔符为逗号 f = open('F://python入门//数据1//红葡萄酒和白葡萄酒//winequality-whole.csv') #read_csv读取时会自动识别表头,数据有表头时不能设置header为空(默认读取第一行,即header=0); #数据无表头时,若不设置header,第一行数据会被视为表头,应传入names参数设置表头名称或设置header=None。 wine = pd.read_csv(f, sep=',', header=0) #将标题行中的空格替换成下划线 wine.columns = wine.columns.str.replace(' ', '_') #将一个字符串赋给变量my_formula,~左侧的变量quality是因变量,波浪线右侧的变量是自变量 my_formula = 'quality ~ alcohol + chlorides + citric_acid + density +fixed_acidity + free_sulfur_dioxide + pH' \ '+ residual_sugar + sulphates + total_sulfur_dioxide + volatile_acidity' #使用公式和数据拟合一个普通最小二乘法模型,并将结果赋值给lm lm = ols(my_formula, data=wine).fit() #创建一个名为dependent_variable的序列来保存质量数据 dependent_variable = wine['quality'] #创建一个名为independent_variables的数据框来保存初始的葡萄酒数据集中除quality、type和in_sample之外的所有变量 #s.difference(t)返回在集合s中但不在t中的元素 independent_variables = wine[wine.columns.difference(['quality', 'type', 'in_sample'])] #使用葡萄酒数据集中的前10个观测创建10个“新”观测,新观测中只包含模型中使用的自变量 #说明,这里使用已经用于拟合的数据,仅出于方便和演示的目的 #isin()函数,首先判断对应的index是否存在,如果不存在则全部为false,存在则为true new_observations = wine.loc[wine.index.isin(range(10)), independent_variables.columns] #基于新观测中的葡萄酒特性预测质量评分 y_predicted = lm.predict(new_observations) # 将真实值和预测值保留两位小数并打印到屏幕上 for each in range(10): print('真实值为:',round(dependent_variable[each],2),'\t预测值为:',round(y_predicted[each],2))
结果:
真实值为: 5 预测值为: 5.0 真实值为: 5 预测值为: 4.92 真实值为: 5 预测值为: 5.03 真实值为: 6 预测值为: 5.68 真实值为: 5 预测值为: 5.0 真实值为: 5 预测值为: 5.04 真实值为: 5 预测值为: 5.02 真实值为: 7 预测值为: 5.3 真实值为: 7 预测值为: 5.24 真实值为: 5 预测值为: 5.69

原文链接:https://blog.csdn.net/qq_45554010/article/details/104537309



