图的遍历

图的遍历

图的遍历，就是按某种方式系统的访问图中的每个顶点而且仅访问一次的过程。 
基本方法分为深度优先遍历和宽度优先遍历两种。

• 深度优先遍历

访问顶点，并将其标记为已访问。 
检查顶点的邻接顶点，从它出发进行深度优先搜索，不存在邻接顶点时回溯。 
重复上述操作，直到从顶点出发的所有顶点都已访问。 
如果图中还存在未访问的顶点，则选出一个未访问过的顶点，由它重复上述的过程，直至所有图中的顶点都被访问过。 
~ 
深度优先搜索序列（DFS序列）：通过深度优先遍历顺序得到的顶点序列。

• 宽度优先遍历

先访问顶点Vi并将其标为已访问。 
依次访问Vi邻接的所有未访问过的顶点，再依次访问与Vi0，Vi1，……Vim-1邻接的所有没被访问的顶点……持续进行下去，直到所有可达顶点都被访问。 
如果图中还存在没被访问过的顶点，则选择一个没被访问过的顶点重复上述步骤。 
~ 
宽度优先搜索序列（BFS序列）：通过宽度优先遍历得到的顶点序列。

例：

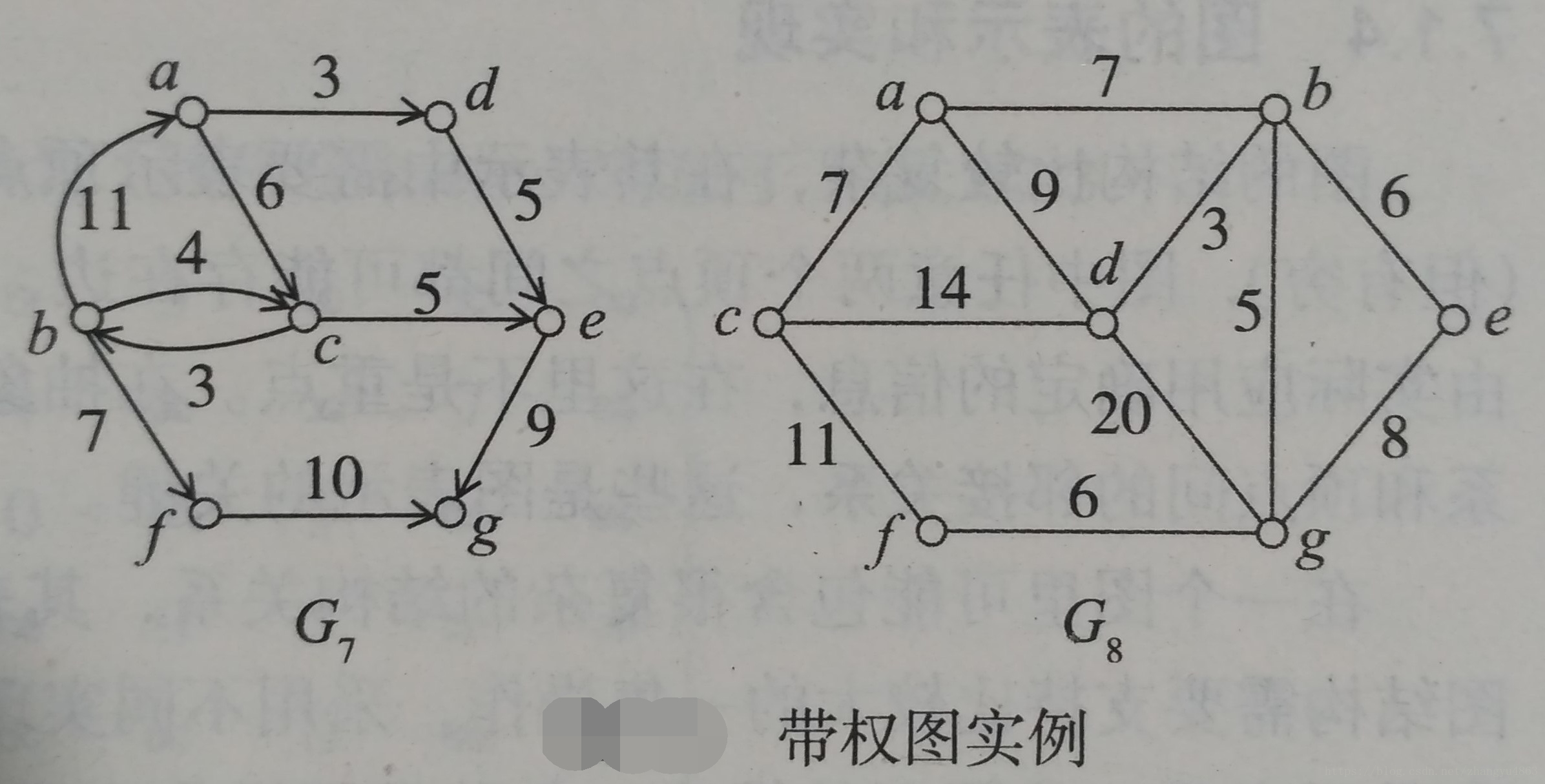
看两个简单的例子，首先考虑图中G7的DFS序列。假设从顶点a出发开始遍历，一个顶点的不同邻接顶点按照a，b，c……的顺序处理。得到的序列是： 
a,c,b,f,g,e,d 
考虑图中G8的BFS序列。采用上面的同样假定，得到的序列是： 
a,b,c,d,e,g,f

def dfs_graph(graph, v0):
    v_num = graph.vertex_num()
    visited = [0] * v_num  # visited记录访问过的顶点
    visited[v0] = 1
    dfs_seq = [v0]  # DFS_seq记录遍历序列
    st = SStack()  # 堆栈
    st.push((0, graph.out_edges(v0)))  # 入栈(i, edges)，说明
    while not st.is_empty():  # 下次应访问边edges[i]
        i, edges = st.pop()
        if i < len(edges):
            v, e = edges[i]
            st.push((i + 1, edges))  # 下次回来将访问edges[i + 1]
            if not visited[v]:  # v未访问，访问并记录其可达顶点
                dfs_seq.append(v)
                visited[v] = 1
                st.push((0, graph.out_edges(v)))
                # 下面访问的边组
    return dfs_seq