二叉搜索树

二叉搜索树

定义

 

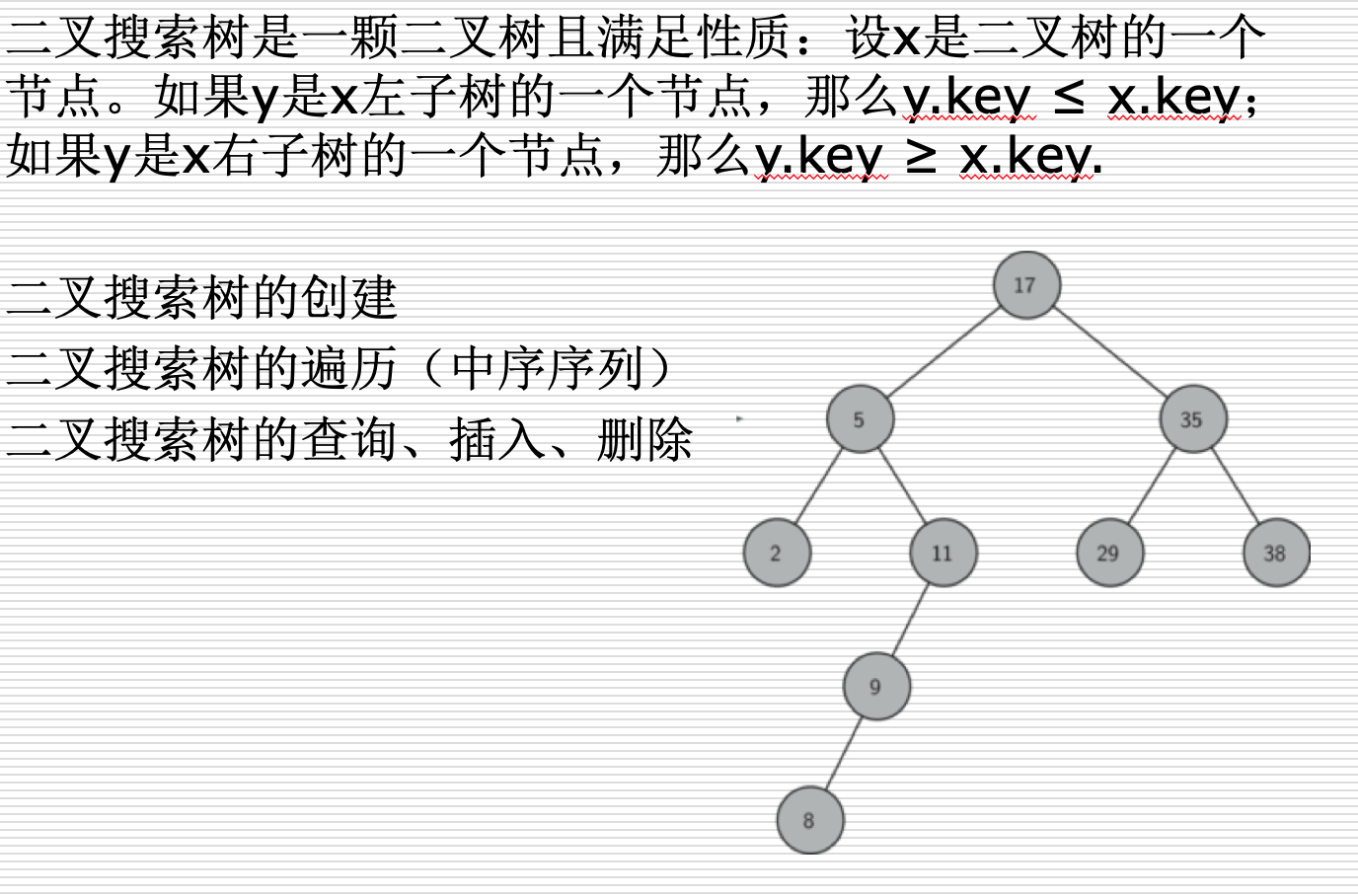
class BiTreeNode:
    def __init__(self, data):
        self.data = data
        self.lchild = None
        self.rchild = None

class BST:
    def __init__(self, li=None):
        self.root = None
        if li:
            for val in li:
                self.insert(val)

    def insert(self, val):
        p = self.root
        if not p:
            self.root = BiTreeNode(val)
            return
        while True:
            if val < p.data:
                if p.lchild:
                    p = p.lchild
                else:
                    p.lchild = BiTreeNode(val)
                    break
            else:
                if p.rchild:
                    p = p.rchild
                else:
                    p.rchild = BiTreeNode(val)
                    break

    def query(self, val):
        p = self.root
        while p:
            if p.data == val:
                return True
            elif p.data > val:
                p = p.lchild
            else:
                p = p.rchild
        return False

def in_order(root):
    if root:
        in_order(root.lchild)
        print(root.data, end=',')
        in_order(root.rchild)

li = [3,5,4,1,6,2,8,7,9]
t = BST(li)
in_order(t.root)

 

中序遍历

二叉搜索树的中序遍历是有序的。

二叉搜索树一般是不会出现相等的情况的，比如数据库的搜索即使B+树，这颗树是自平衡的二叉搜索树！

一般不会出现相等的情况，如果有相等的情况的话，可以写一个判断让其在左子树还是右子树。

 

二叉搜索树的效率

 

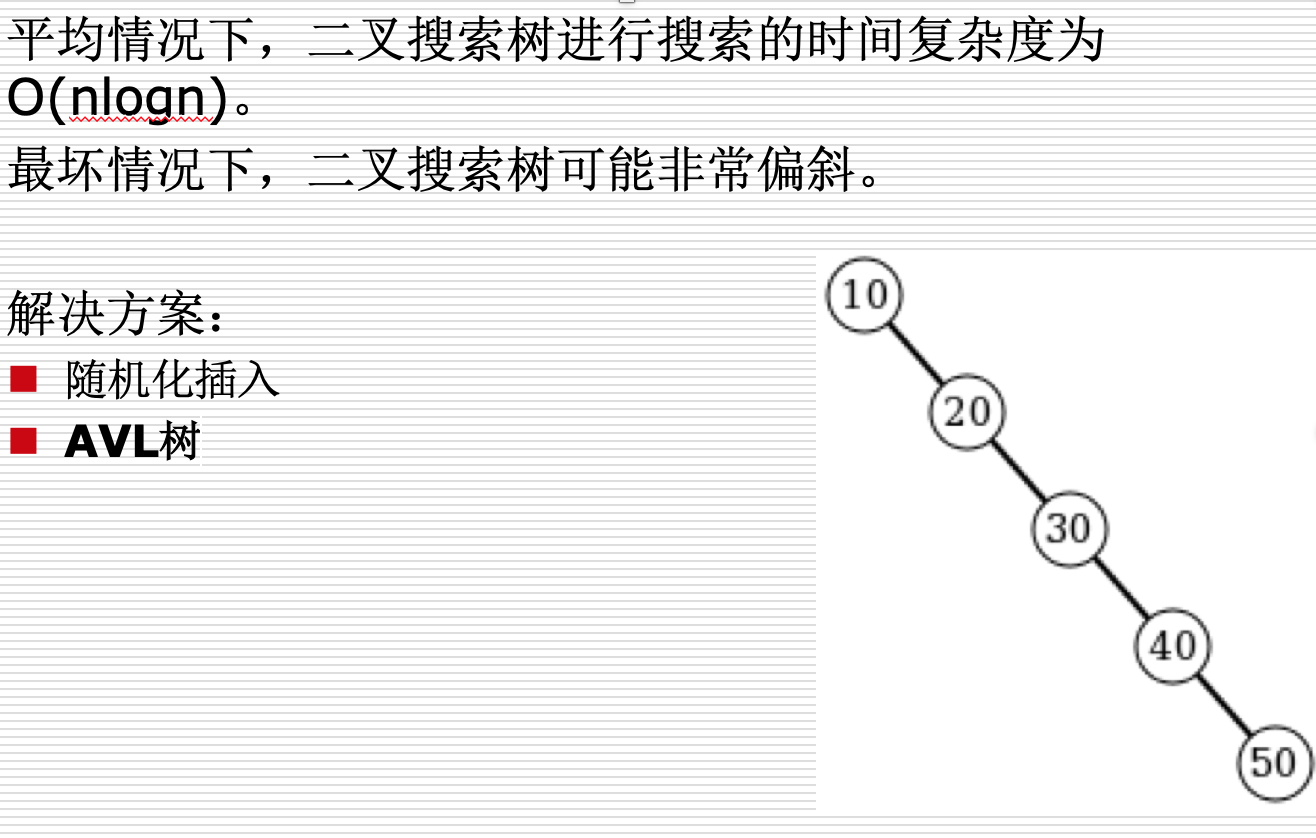
 删除操作

 

 

 

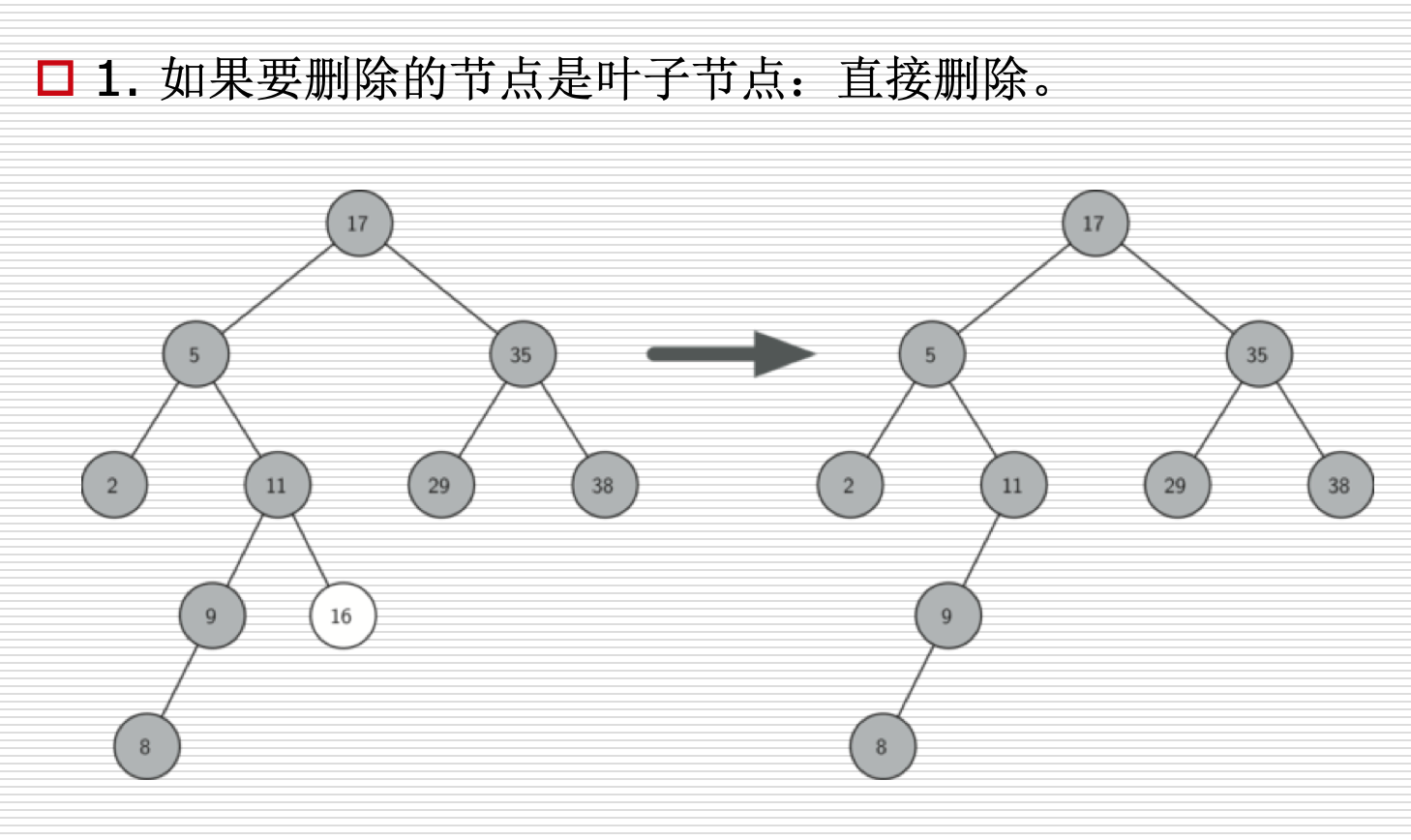
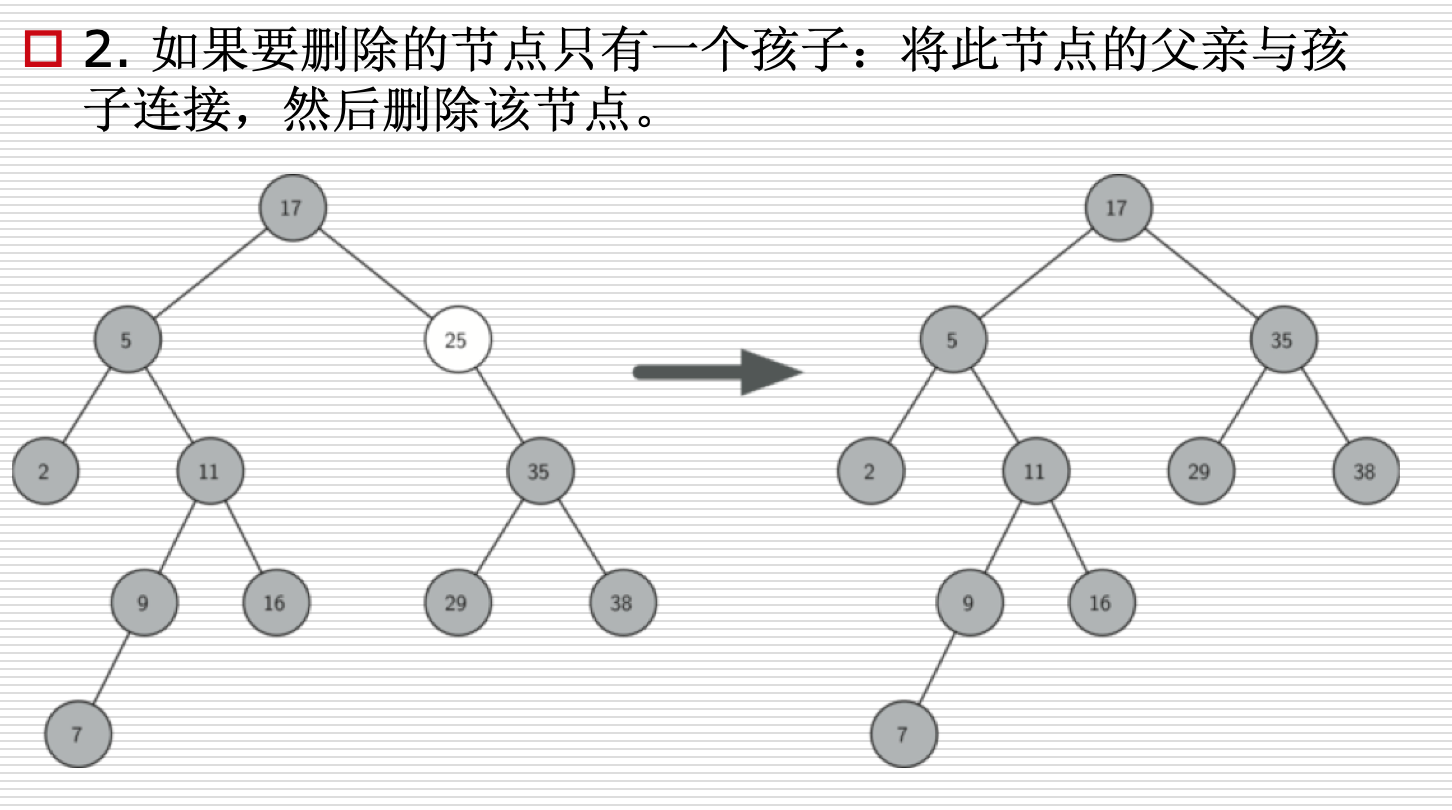
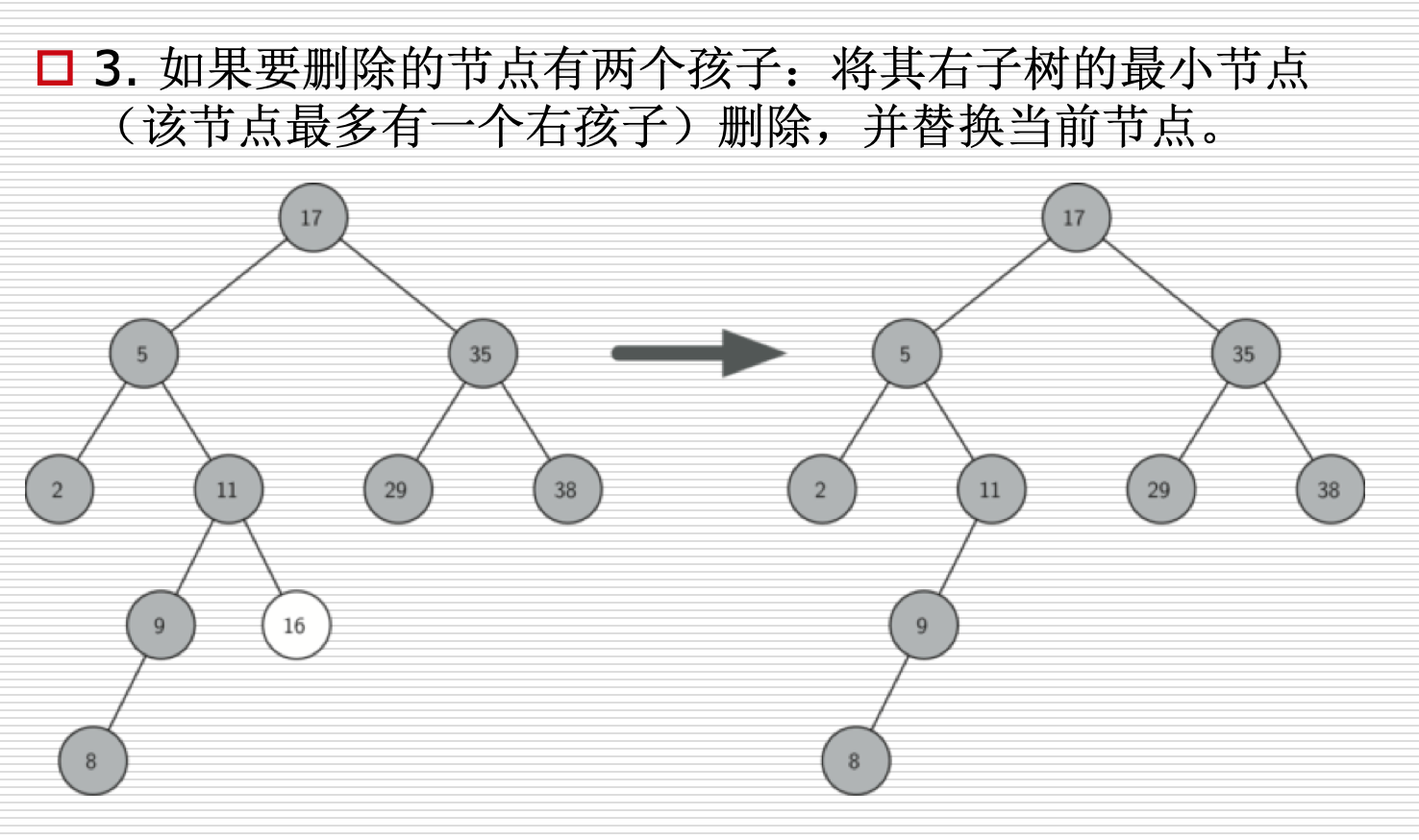
 代码实现

import random

class BiTreeNode:
    def __init__(self, data):
        self.data = data
        self.lchild = None
        self.rchild = None
        self.parent = None

class BST:
    def __init__(self, li=None):
        self.root = None
        if li:
            for val in li:
                self.insert_no_rec(val)

    def insert(self, root, val):
        if root is None:
            root = BiTreeNode(val)
        elif val < root.data:
            root.lchild = self.insert(root.lchild, val)
            root.lchild.parent = root
        elif val > root.data:
            root.rchild = self.insert(root.rchild, val)
            root.rchild.parent = root
        return root

    def insert_no_rec(self, val):
        p = self.root
        if not p:
            self.root = BiTreeNode(val)
            return
        while True:
            if val < p.data:
                if p.lchild:
                    p = p.lchild
                else:
                    p.lchild = BiTreeNode(val)
                    p.lchild.parent = p
                    break
            elif val > p.data:
                if p.rchild:
                    p = p.rchild
                else:
                    p.rchild = BiTreeNode(val)
                    p.rchild.parent = p
                    break
            else:
                return

    def query(self, root, val):
        if not root:
            return None
        if root.data == val:
            return root
        elif root.data > val:
            return self.query(root.lchild, val)
        else:
            return self.query(root.rchild, val)

    def query_no_rec(self, val):
        p = self.root
        while p:
            if p.data == val:
                return p
            elif p.data > val:
                p = p.lchild
            else:
                p = p.rchild
        return None


    def in_order(self, root):
        if root:
            self.in_order(root.lchild)
            print(root.data, end=',')
            self.in_order(root.rchild)

    def pre_order(self, root):
        if root:
            print(root.data, end=',')
            self.pre_order(root.lchild)
            self.pre_order(root.rchild)


    def _remove_node_1(self, node):
        if not node.parent:  # 根节点
            self.root = None
        elif node == node.parent.lchild:  # 是父亲的左孩子
            node.parent.lchild = None
        else:  # 是父亲的右孩子
            node.parent.rchild = None

    def _remove_node_21(self, node):
        if not node.parent:  # 根节点
            self.root = node.rchild
            self.root.parent = None
        elif node == node.parent.lchild:
            node.parent.lchild = node.rchild
            node.rchild.parent = node.parent
        else:
            node.parent.rchild = node.rchild
            node.rchild.parent = node.parent

    def _remove_node_22(self, node):
        if not node.parent:  # 根节点
            self.root = node.lchild
            self.root.parent = None
        elif node == node.parent.lchild:
            node.parent.lchild = node.lchild
            node.lchild.parent = node.parent
        else:
            node.parent.rchild = node.lchild
            node.lchild.parent = node.parent

    def delete(self, val):
        if self.root: # 不是空树
            node = self.query_no_rec(val)
            if not node:    # 如果不存在该节点
                return False
            if not node.lchild and not node.rchild: # 1.叶子节点
                self._remove_node_1(node)
            elif not node.lchild:   # 2.1 只有一个右孩子
                self._remove_node_21(node)
            elif not node.rchild:   # 2.2 只有一个左孩子
                self._remove_node_22(node)
            else:               # 3. 有两个孩子
                # 找到右子树中的最小节点
                min_node = node.rchild
                while min_node.lchild:
                    min_node = min_node.lchild
                node.data = min_node.data
                # 删除该节点
                if min_node.rchild:
                    self._remove_node_21(min_node)
                else:
                    self._remove_node_1(min_node)

#
#
# li = [7,0,3,8,6,2,9,4,1,5]
# tree = BST(li)
#
# tree.delete(7)
# tree.delete(0)
#
#
# tree.in_order(tree.root)
#print(tree.query_no_rec(12))