数据结构之排序

排序

排序，就是重新排列表中的元素，使表中的元素按关键字有序的过程。

排序主要分为以下几种排序

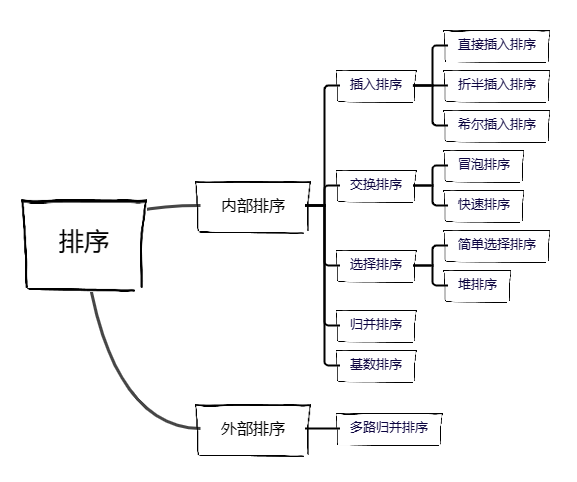
以下将用c语言编写排序算法

直接插入排序

一种最简单的排序方法，其基本操作是将一条记录插入到已排好的有序表中，从而得到一个新的、记录数量增1的有序表

以下是示例:

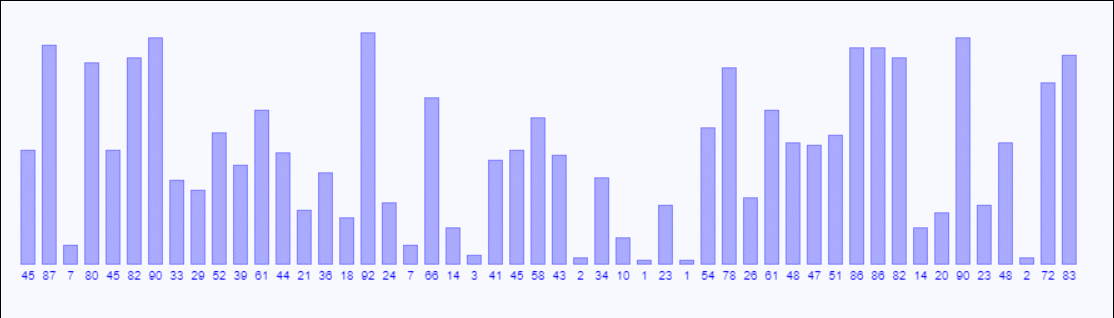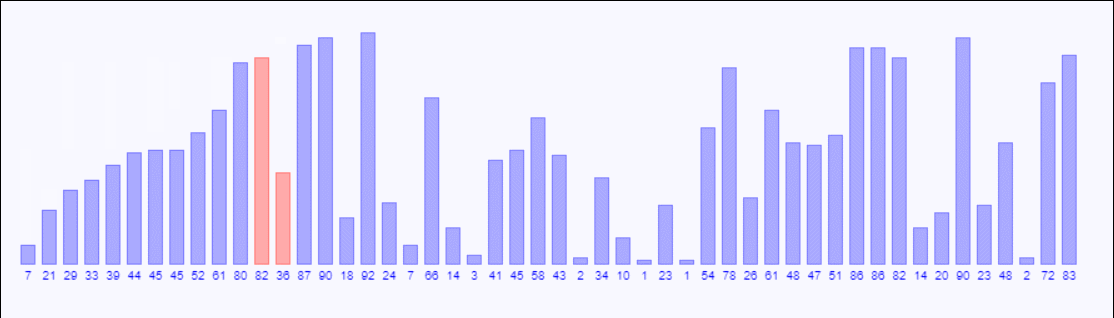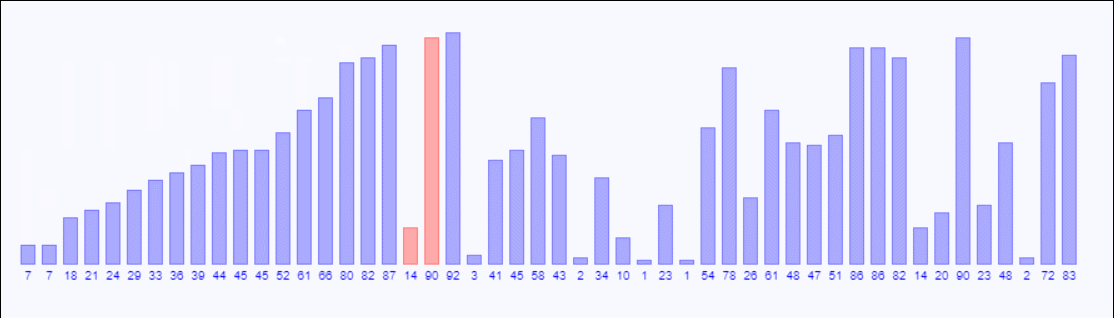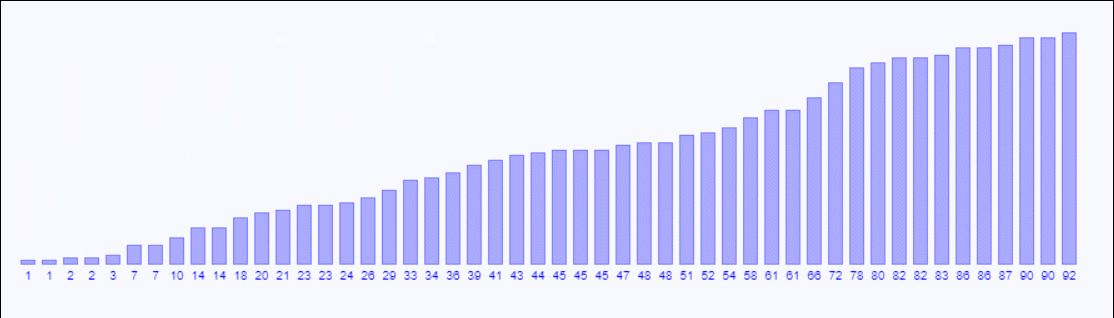
void insertSort(int list[],int arraySize){
	for(int i=1;i<arraySize;i++){
		if(list[i]<list[i-1]){
			int temp=list[i],j;
			for(j=i-1;temp<list[j]&&j>=0;j--)
				list[j+1]=list[j];
		
			list[j+1]=temp;
		}
	} 
}

时间复杂度为O(n^2) 空间复杂度O(1)

折半插入算法

折半插入排序是对直接插入排序的一种改良方式，在直接插入排序中，每次向已排序序列中插入元素时，都要去寻找插入元素的合适位置，但是这个过程是从已排序序列的最后开始逐一去比较大小的，这其实很是浪费，因为每比较一次紧接着就是元素的移动。折半排序就是通过折半的方式去找到合适的位置，然后一次性进行移动，为插入的元素腾出位置。什么是折半的方式去找合适的位置呢，那就是折半查找了，因为再已排序的序列中，序列元素都是按照顺序排列的，既然这样，完全不需要逐一去比较大小，而是去比较已排序序列的中位数，这个中间的位置将一排序列分为左右两部分，通过一次比较后，就缩小了比较的范围，重复这样的操作，需要插入的元素就找到了合适的位置了。

void BinsertSort(int list[],int arraySize){
	for(int i=1;i<arraySize;i++){
		int temp=list[i];
		int low=0;
		int high=i-1;
		while(low<=high){
			int mid=(low+high)/2;
			if(temp<list[mid])
				high=mid-1;
			else
				low=mid+1;
		}
		for(int j=i;j>=low+1;j--)
			list[j]=list[j-1];
		
		list[low]=temp;
	}
}

时间复杂度为O(n^2) 空间复杂度O(1)

希尔排序

希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因DL．Shell于1959年提出而得名。希尔排序是记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。

以下是示例:

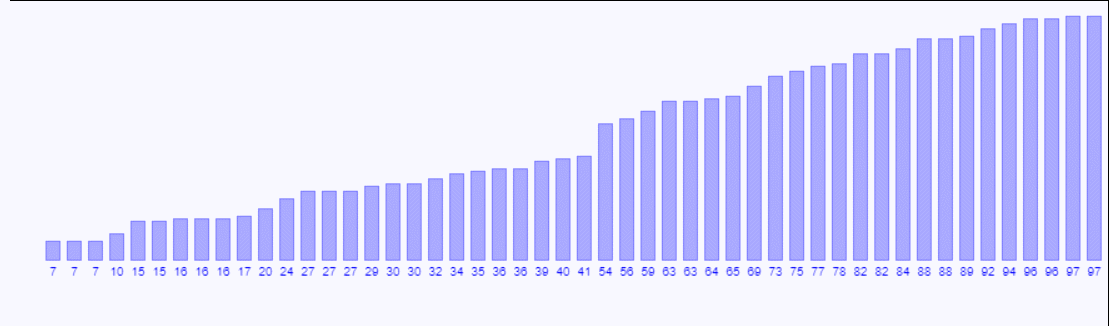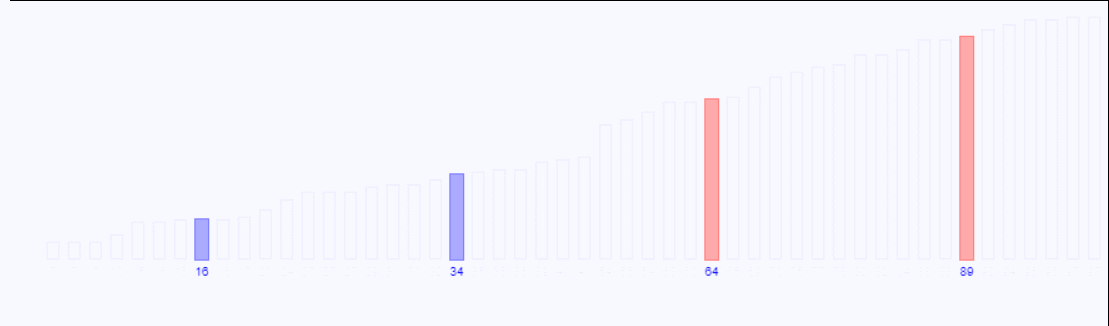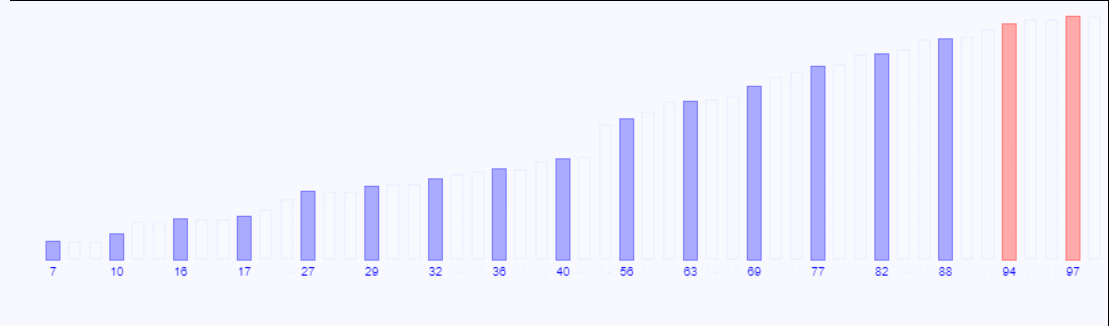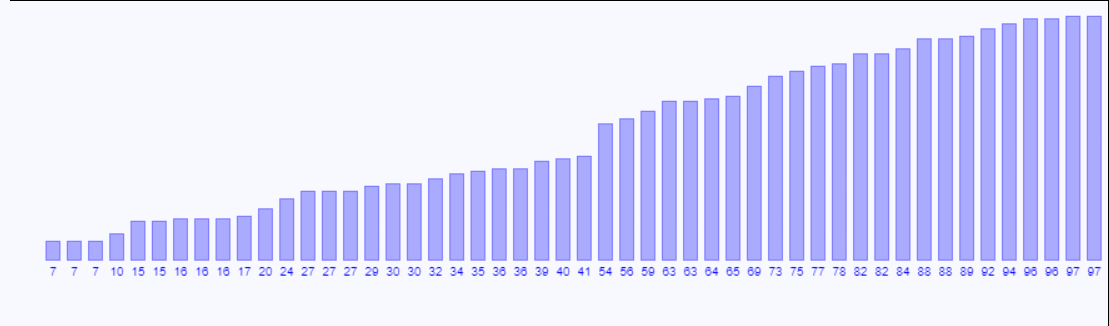
void shellSort(int list[],int arraySize){
	int gap,i,j,temp;
	for(gap=arraySize/2;gap>=1;gap/=2)
		for(i=gap;i<arraySize;i++){
			if(list[i]<list[i-gap]){
				temp=list[i];
				for(j=i-gap;j>=0&&temp<list[j];j=j-gap)
					list[j+gap]=list[j];
				
				list[j+gap]=temp;
			}
		} 
}

时间复杂度：由于希尔排序的时间复杂度依赖于增量序列的函数，这涉及数学上尚未解决的难题，所以其时间复杂度分析比较困难。当n在某个特定范围时，希尔排序的时间复杂度约为O(n^{1.3)。在最坏的情况下希尔排序的时间复杂度为O(n}2)。

空间复杂度：O(1)

冒泡排序

1. 比较相邻的元素。如果第一个比第二个大，就交换它们两个。
2. 对每一对相邻的元素都进行比较，等所有的比较完后最后一个数字是这堆数据里的最大数字。
3. 重复步骤一，直到排序完成。

以下是示例:

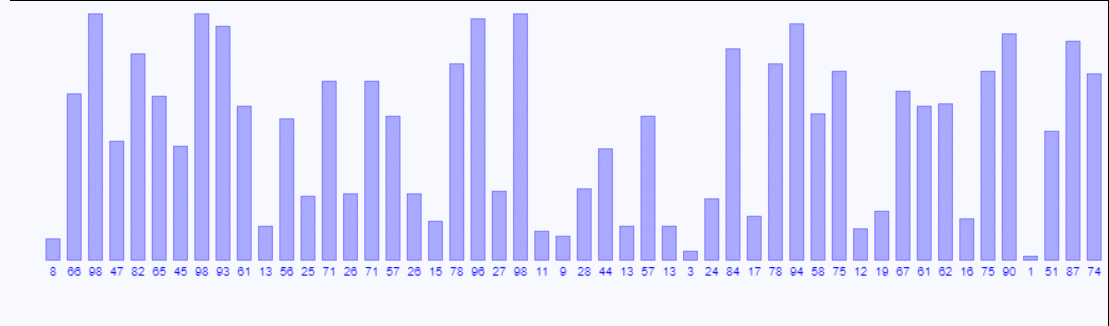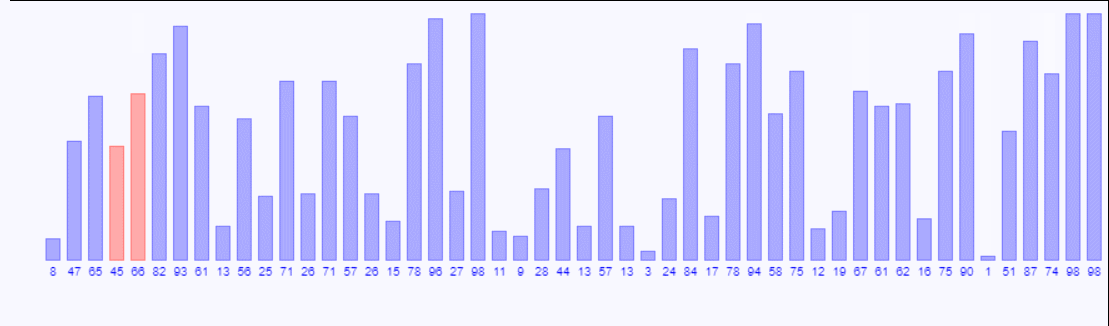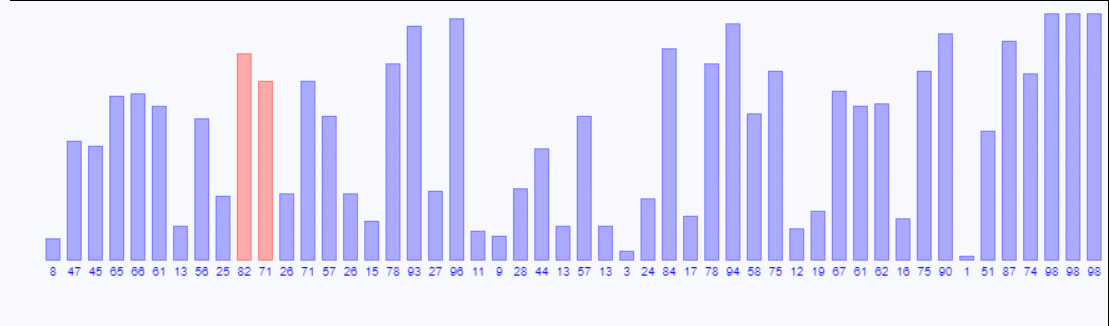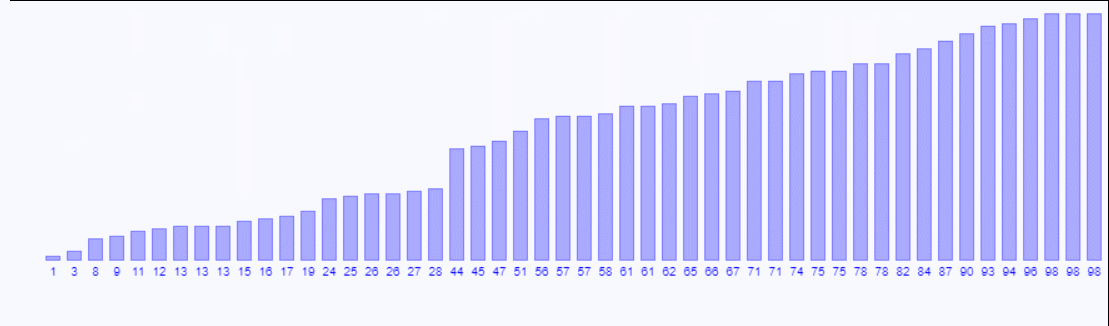
void bubbleSort(int list[],int arraySize){
	for(int i=arraySize-1;i>0;i--){
		for(int j=0;j<i;j++){
			if(list[j]>list[j+1]){
				int temp=list[j];
				list[j]=list[j+1];
				list[j+1]=temp;
			}
		}
	}
}

时间复杂度O(n^2) 空间复杂度O(1)

快速排序

1. 先从数组中选取一个数作为基准点，可随机选择；
2. 将数组中大于该基准点的放在该基准点右边，小于该基准点的放在该基准点左边；
3. 对左右两个数组进行快速排序。

以下是示例：

void quickSort(int list[],int low,int high){
	int i=low,j=high,key=list[low],temp;
	if(i>j) return ;
	while(i<j){
		while(list[j]>=key&&i<j) j--;
		while(list[i]<=key&&i<j) i++;
		if(i<j){
			temp=list[j];
			list[j]=list[i];
			list[i]=temp;
		}
	}
	list[low]=list[i];
	list[i]=key;
	
	quickSort(list,low,i-1);
	quickSort(list,i+1,high);
}

时间复杂度O(n*logn) 空间复杂度O(logn) 注：logn应该是log以2为底n，只是没办法打出来所以用logn代替

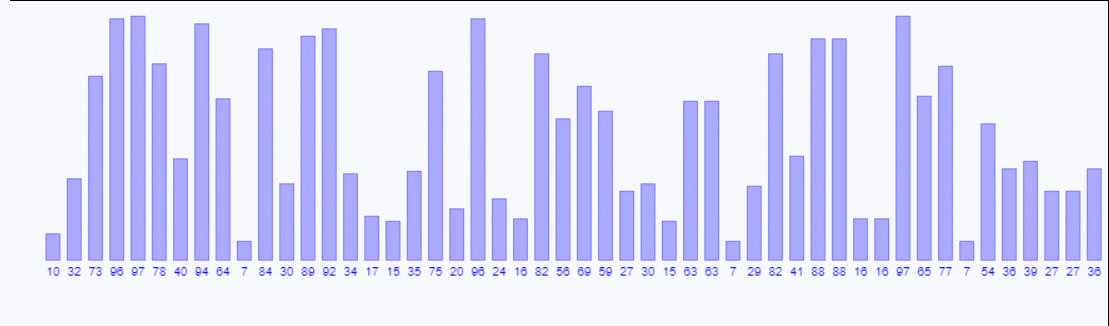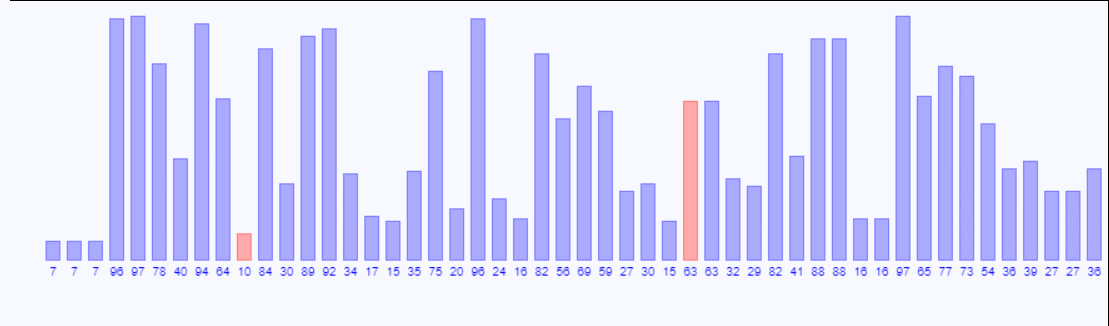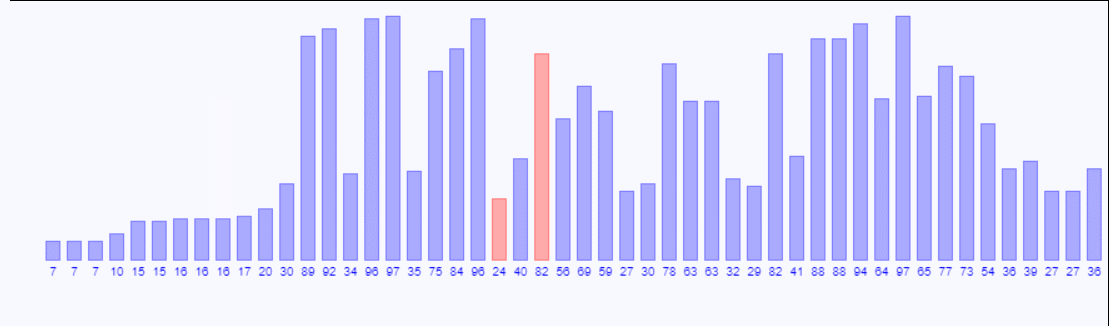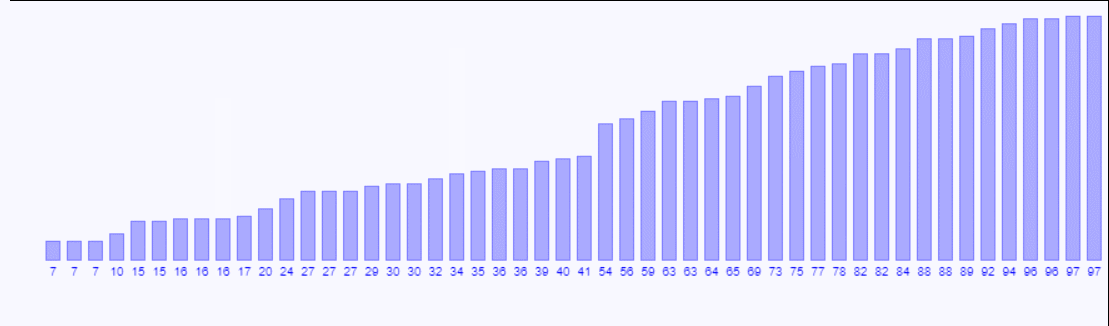
简单选择排序

简单选择排序是最简单直观的一种算法，基本思想为将序列分为有序序列和待排的无序序列，每一趟从后面n-i个待排数据元素中选择最小的一个元素作为有序序列的第i个元素，直到所有元素排完为止。

以下是示例:

void selectSort(int list[],int arraySize){
	for(int i=0;i<arraySize-1;i++){
		int	min=i;
		for(int j=i+1;j<arraySize;j++){
			if(list[j]<list[min]) min=j;
		}
		if(min!=i){
			int temp=list[min];
			list[min]=list[i];
			list[i]=temp;
		}
	}
}

时间复杂度O(n^2) 空间复杂度O(1)

堆排序

1.首先将待排序的数组构造成一个大根堆，此时，整个数组的最大值就是堆结构的顶端

2.将顶端的数与末尾的数交换，此时，末尾的数为最大值，剩余待排序数组个数为n-1

3.将剩余的n-1个数再构造成大根堆，再将顶端数与n-1位置的数交换，如此反复执行，便能得到有序数组

以下是示例:

void Swap(HDataType* num1, HDataType* num2)
{
	HDataType tmp = *num1;
	*num1 = *num2;
	*num2 = tmp;
}

//建大堆的向下调整
void AdjustDown(HDataType* data, size_t size, size_t pos)//pos是要进行向下调整的数的下标
{
	assert(data);
	
	size_t parent = pos;
	size_t child = parent * 2 + 1;
	while (child < size)//若孩子节点的下标小于数组长度，则循环继续
	{
		if (child + 1 < size && data[child + 1] > data[child])//若右孩子	存在并且右孩子大于左孩子，则修改child，将child指向右孩子
		{
			child++;
		}
		if (data[parent] < data[child])//若父节点小于子节点，交换两节点
		{
			Swap(&data[parent], &data[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;//若父节点大于子节点，满足堆的性质，不用调整
		}
	}
}

void HeapSort(HDataType* data, size_t size)
{
	assert(data);
	for (int i = (size - 2) / 2; i >= 0; i--)
	{
		AdjustDown(data, size, i);
	}
	while (size > 0)
	{
		Swap(&data[0], &data[size - 1]);
		size--;
		AdjustDown(data, size, 0);
	}
}

时间复杂度O(nlogn) 空间复杂度O(1)

归并排序

归并排序，是创建在归并操作上的一种有效的排序算法。算法是采用分治法（Divide and Conquer）的一个非常典型的应用，且各层分治递归可以同时进行。归并排序思路简单，速度仅次于快速排序，为稳定排序算法，一般用于对总体无序，但是各子项相对有序的数列。

• 分解（Divide）：将n个元素分成个含n/2个元素的子序列。
• 解决（Conquer）：用合并排序法对两个子序列递归的排序。
• 合并（Combine）：合并两个已排序的子序列已得到排序结果。

以下是示例：

void merge_sort_recursive(int arr[], int reg[], int start, int end) {
    if (start >= end)
        return;
    int len = end - start, mid = (len >> 1) + start;
    int start1 = start, end1 = mid;
    int start2 = mid + 1, end2 = end;
    merge_sort_recursive(arr, reg, start1, end1);
    merge_sort_recursive(arr, reg, start2, end2);
    int k = start;
    while (start1 <= end1 && start2 <= end2)
        reg[k++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++];
    while (start1 <= end1)
        reg[k++] = arr[start1++];
    while (start2 <= end2)
        reg[k++] = arr[start2++];
    for (k = start; k <= end; k++)
        arr[k] = reg[k];
}

void merge_sort(int arr[], const int len) {
    int reg[len];
    merge_sort_recursive(arr, reg, 0, len - 1);
}

时间复杂度O(nlogn) 空间复杂度O(n)

基数排序

基数排序是按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位。有时候有些属性是有优先级顺序的，先按低优先级排序，再按高优先级排序。最后的次序就是高优先级高的在前，高优先级相同的低优先级高的在前。

原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。基数排序的方式可以采用LSD（Least significant digital）或MSD（Most significant digital），LSD的排序方式由键值的最右边开始，而MSD则相反，由键值的最左边开始。

各种排序的算法性质

算法种类	时间复杂度	空间复杂度	是否稳定
直接插入排序	O(n^2)	O(1)	是
冒泡排序	O(n^2)	O(1)	是
简单选择排序	O(n^2)	O(1)	否
希尔排序	-	O(1)	否
快速排序	O(nlogn)	O(logn)	否
堆排序	O(nlogn)	O(1)	否
2路归并排序	O(nlogn)	O(n)	是
基数排序	O(d(n+r))	O®	是

var code = “dba3cfa0-fb79-4d03-8725-bcd930f69a50”