树和二叉树知识要点(期末必考)
树和二叉树
什么是树?
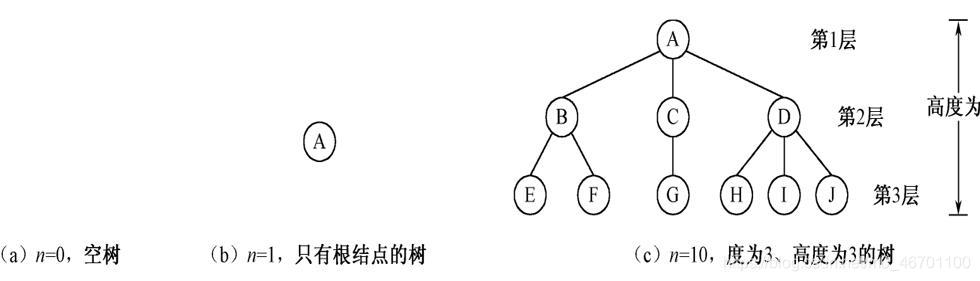
树是由n(n>=0)个节点组成的有限集合(树中元素通常称为节点)。n=0的树称为空树;
树形结构是非线性数据结构。
根:一个特殊的节点,它只有后继结点,没有前驱结点。
子树:除根节点外的其他节点分为m个互不相交的结点,其中每个集合为根的子树。
有序树:子树之间映射客观存在的次序关系(子树次序不能调换)。
无序树:子树之间不存在次序关系,即子树次序能够调换。
森林: m(m≥0)棵互不相交的树的集合。
结点的知识
结点:包含了数据元素及若干个指向其子树的分支。
结点的度:结点的子树数目或分支个数。
树的度:在树中取各结点的度的最大值.
分支结点(又称非终端结点):度大于零的结点。
叶子结点(又称终端结点):度为零的结点。
结点的路径:根结点到该结点所经分支和结点构成结点的路径。
结点的路径长度:根结点到该结点路径上所经分支的数目。
结点的层次:设根结点的层次为1,则其子树的根结点层次为2:第L层结点的子树的根结点层次为L+1.
树的深度:树中结点(该结点必为树叶结点)的最大层次。
孩子结点及双亲结点:结点的子树的根结点称为该结点的孩子结点,该结点又称为孩子结点的双亲结点。
兄弟结点:拥有同一个双亲结点的若干个结点互称为兄弟结点。
堂兄弟结点:在同一层次上, 但双亲结点不同的若干个结点称为堂兄弟结点。
祖先结点:根结点到该结点路径上的所有结点均为该节点的相先结点。
子孙结点:某结点的于树中所包含的所有结点均为该结点的子孙结点。
二叉树
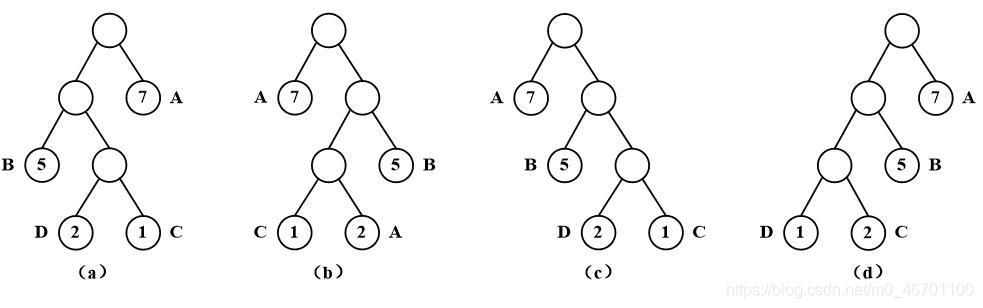
二叉树:n(n>=0)个结点的有限集,当n=0时,二叉树为空;
当n>0时,二叉树由一个根结点及至多两颗互不相交的左右子树组成,且左右子树都是二叉树。
特殊二叉树:
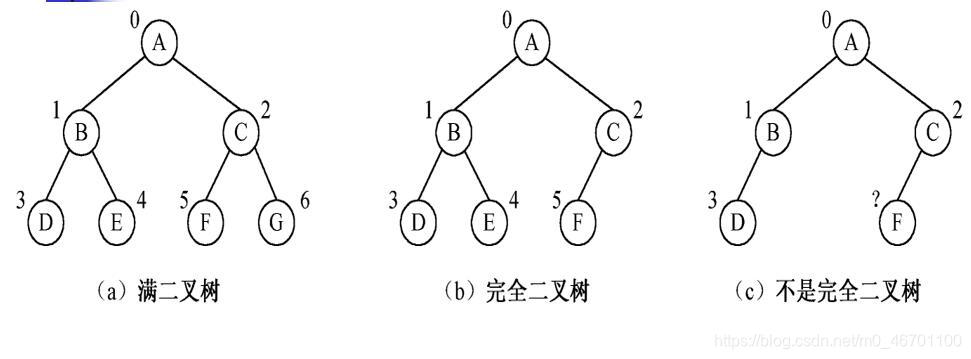
满二叉树:一颗深度为k的二叉树若每一层上的结点数都达到最大
完全二叉树:一颗具有n个结点且深度为k的二叉树若前k-1层的结点数都达到最大,剩余的结点在第k层中从左至右连续分布
二叉树的性质
二叉树的性质1:在二叉树的第i层上至多有2^i-1个结点(i≥1)。
二叉树的性质2:深度为k的二叉树至多有2*-1个结点(k≥1)。
二叉树的性质3:对任意的一棵二叉树,如果其终端结点数为n0,度为2的结点数为n2,则有n0=n2+1。
二叉树的性质4:具有n个结点的完全二叉树的深度为[lbn]+1。
二叉树的性质5:如果对一棵具有 n个结点的完全二叉树从1到n对每一结点进行层序编号,则有:
①若i=1,则第i个结点是二叉树的根,无双亲。若i>1,则其双亲结点的位置是i/2。
②若2i>n,则第i个结点为叶子结点,无左孩子;否则,其左孩子结点的位置是2i。
③若2i+1>n,则第i个结点无右孩子;否则,其右孩子结点的位置是2i+1。
二叉树的遍历
1.先序遍历(DLR)若树不空,则先访问根结点,然后依次先根遍历各棵子树。
2.中序遍历(LDR)
3.后序遍历(LRD) 若树不空,则先依次后根遍历各棵子树,然后访问根结点。
4.层次遍历 :若树不空,则自上而下自左至右访问树中每个结点。
Huffman树
各路径的定义
结点的路径长度定义为:从根结点到该结点的路径上分支的数目。
树的路径长度定义为:树中每个结点的路径长度之和。
树的带权路径长度定义为: 树中所有叶子结点的带权路径长度之和。
注: 在所有含 n 个叶子结点、并带相同权值的 m 叉树中,必存在一棵其带权路径长度取最小值的树,称为“最优树”(哈夫曼树)。
哈夫曼树定义:为带权外路径长度最短的二叉树。
哈夫曼树不唯一