数据挖掘:关联规则
1. 基本概念
1.1 事务与项集
事务(transaction):关联规则分析的对象,可以理解为一种商业行为;事务由序号和项集组成,序号是唯一确定一个事物的标志;
项集:数据库中的数据项构成的非空集合。顾客购买行为是一种包含多个商品购买的事务。二一种商品可以视为一个项目;若干个项目的集合简称未项集。若项集包含k个项目,则称该项集未k-项集;
例:
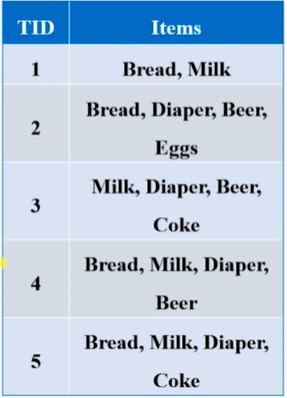
上图表示某超市的五个购物篮中的物品,TID唯一标识一个事务,即一个购物篮表示一个事务;TID为1的事务中有两种商品,一种商品视为一个项目,则这有两个项目,成为2-项集;
上图可知,共有五个事务,其中有4个4-项集,1个2-项集。
1.2 支持度计数
包含特定项集的事务个数(即从各项食物中的特定项集为子集的事务个数);
如:k({Milk,Bread})=3
1.3 支持度、置信度、关联规则
支持度:包含项集的事务数与总事务数的比值;
如:s({Milk,Bread})=3/5
置信度:是事务集中同时包含X和Y的事务数量与包含X的事务数量之比,记为confidence(X=>Y),置信度反映了包含X的事务中出现Y的条件概率。即confidence(X=>Y)=support(XUY)/support(X)=P(XY)
如:
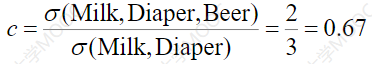
关联规则:形如X→Y的蕴含表达式,其中X和Y分别是一事务的真子集,且X∩Y=Φ。X称为规则的前提,Y称为规则的结果。关联规则反映出X中的项目在事务出现时,Y中的项目也跟着出现的规律。
关联规则表示不同项目集合之间的相互依存性和关联性;
支持度可用于衡量规则在数据库中出现的概率(确定项集的频繁程度);
置信度用于衡量规则的强弱程度,置信度越高,说明X出现时,Y出现的可能性越高。
1.4 最小支持度、最小置信度、强关联规则
最小支持度:用户定义的衡量支持的一个阈值;表示项目集在统计意义上的最低重要性;
最小置信度:用户定义的衡量支持的一个阈值;表示关联规则的最低可靠性;
强关联规则:频繁项集的基础上大于等于最小支持度/置信度称为强关联规则;
注:
(1)如果支持度和置信度闭值设置的过高,虽然可以减少挖掘时间,但是容易造成一些隐含在数据中非频繁特征项被忽略掉,难以发现足够有用的规则;
(2)如果支持度和置信度闭值设置的过低,又有可能产生过多的规则,甚至产生大量冗余和无效的规则,同时由于算法存在的固有问题,会导致高负荷的计算量,大大增加挖掘时间。
1.5 频繁项集与项目集格空间理论
频繁项集:是满足最小支持度阈值的所有项集;
最大频繁项集:不被其他频繁项集包含的频繁项集称为最大频繁项集;
项目集格空间理论:频繁项集的所有子集仍是频繁项集;非频繁项集的所有超集市非频繁项集。
1.6 关联分析
用于挖掘大规模数据集中有意义和有价值的联系;
通常用关联规则或频繁项集的形式表示;
2. Apriori算法原理
2.1 算法思想
基本思想是通过对数据库的多次扫描来计算项集的支持度,发现所有的频繁项集从而生成关联规则。Apriori算法对数据集进行多次扫描,第一次扫描得到频繁一项集L1,第k(k>1)次扫描首先利用第k-1次扫描的结果k(k-1)来产生候选k项集的集合Ck,然后再扫描过程中确定Ck中元素的支持度,最后在每一次扫描结束时计算频繁k项集的集合Lk,算法在当候选k项集的集合Ck为空时结束。
例:
已知阴影项集{2,3}是非频繁的。利用这个知识,我们就知道项集{0,2,3},{1,2,3}以及{0,1,2,3}也是非频繁的。也就是说,一旦计算出了{2,3}的支持度,知道它是非频繁的后,就可以紧接着排除{0,2,3}、{1,2,3}和{0,1,2,3}。
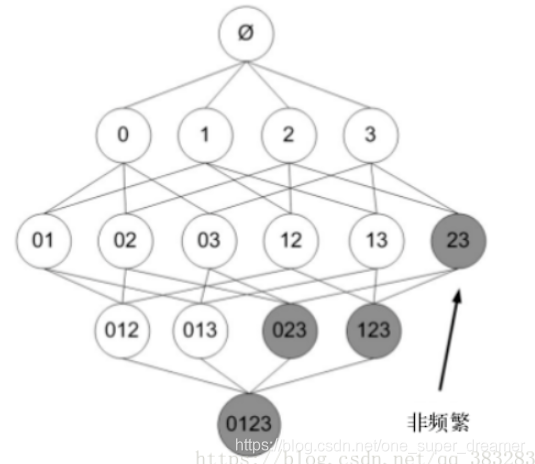
2.2 Apriori算法产生频繁项集
产生频繁项集的过程主要分为连接和剪枝两步:
(1)连接步:为找到Lk(k≥2),通过(k-1)与自身连接产生产生候选k项集的集合Ck。自身连接时,两个项集对应的想按从小到大顺序排列好,当前除最后一项外的其他项都相等时,两个项集可连接,连接产生的结果为(l1[1], l1[2], …, l1[k-1], l2[k-2])。
(2)剪枝步:由Apriori算法的性质可知,频繁k项集的任何子集必须是频繁项集。由连接步产生的集合Ck需进行验证,除去不满足支持度的非频繁k项集。
2.3 Apriori算法的基本步骤
(1)扫描全部数据,产生候选1项集的集合C1;
(2)根据最小支持度,由候选1项集的集合C1产生频繁1项集的集合L;
(3)对k>1,重复执行步骤
(4)由Lk执行连接和剪枝操作,产生候选(k+1)-项集的集合C(k+1)。
(5)根据最小支持度,由候选(k+1)-项集的集合C(k+1),产生频繁(k+1)-项集的集合L(k+1);
(6)若L≠Ф,则k=k+1,跳往步骤(4);否则往下执行;
(7)根据最小置信度,由频繁项集产生强关联规则,程序结束。
2.4 Apriori例题
设置最小支持度为2,写出利用Apriori算法产生候选项集及频繁项集的过程。

第一次搜索:

第二次搜索:
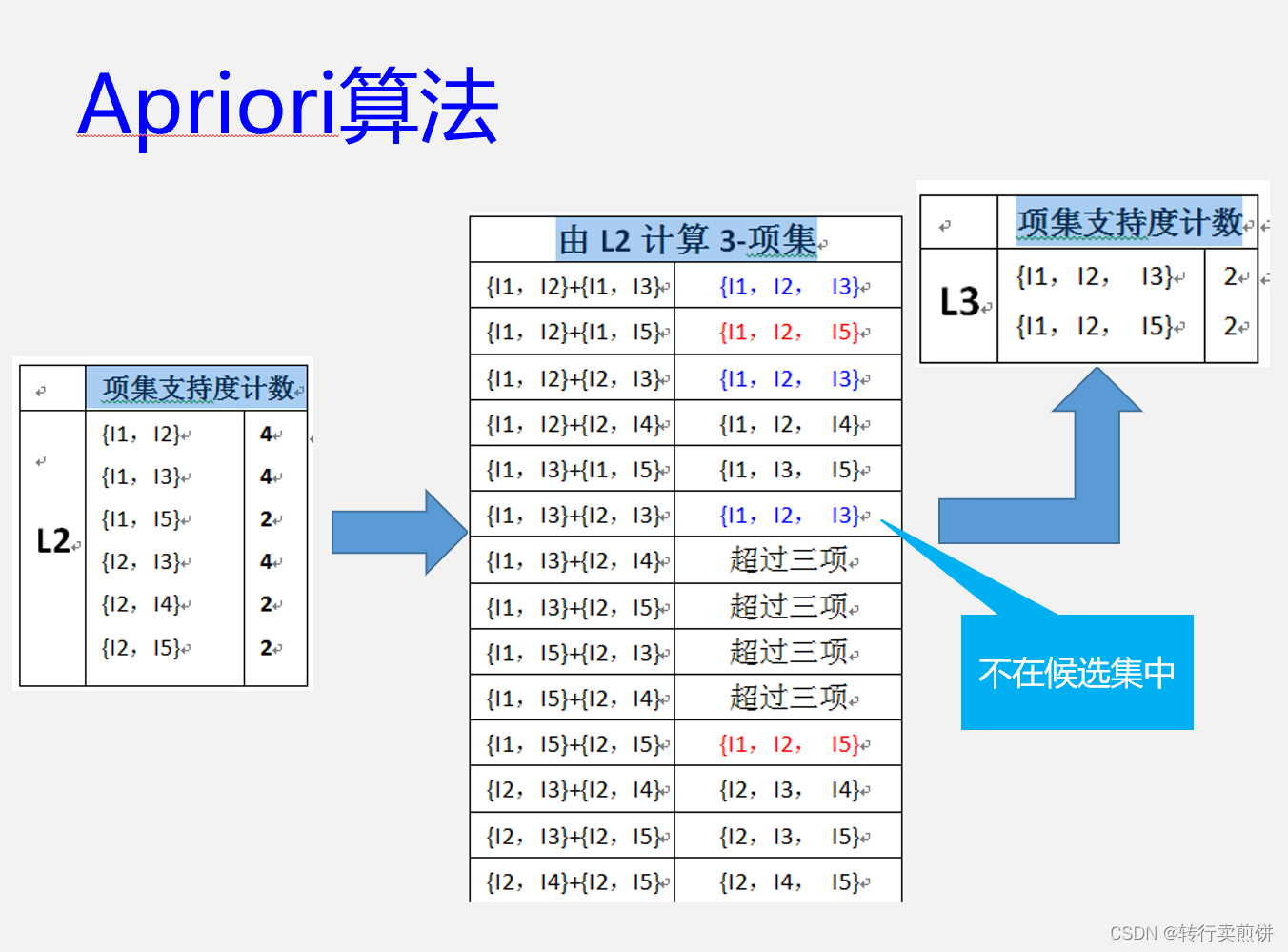

一旦由数据库D中的事务找出频繁项集,由它们产生的强关联规则是直接的。
频繁集L1={I1, I2, I5},L1的非空子集有{I1, I2},{I1, I5},{I2, I5},{I1},{I2},{I5}
I1^ I2 => I5, confidence=2/4=50%
I1 ^ I5 => I2, confidence=2/2=100 %
I2 ^ I5 => I1, confidence=2/2=100 %
I1 => I2 ^ I5, confidence=2/6=33 %
I2 => I1 ^ I5, confidence=2/7=29 %
I5 => I1 ^ I2, confidence=2/2=100 %
最小置信度阈值未70%,则只有第2,3和最后存在强关联规则。
频繁集L2={I1, I2, I3},L2的非空子集有{I1, I2}, {I1, I3}, {I2, I3}, {I1}, {I2}, {I3}
I1^ I2 => I3, confidence=2/4=50%
I1 ^ I3 => I2, confidence=2/4=50 %
I2 ^ I3 => I1, confidence=2/4=50%
I1 => I2 ^ I3, confidence=2/6=33 %
I2 => I1 ^ I3, confidence=2/7=29 %
I3 => I1 ^ I2, confidence=2/6=33 %
不满足强关联规则。
3. FP-growth算法
将数据集存储在一个特定的称作FP树的结构之后发现频繁项集或频繁项对,即常在一块出现的元素项的集合FP树。
FP-growth算法比Apriori算法效率更高,在整个算法执行过程中,只需遍历数据集2次,就能够完成频繁模式发现,其发现频繁项集的基本过程:①构建FP树;②从FP树种挖掘频繁项集;
3.1 FP-growth的一般流程
1. 先扫描一遍数据集,得到频繁项为1的项目集,定义最小支持度(项目出现最少次数),删除那些小于最小支持度的项目,然后将原始数据集中的条目按项目中降序进行排列。
2. 第二次扫描,创建项头表(从上往下降序),以及FP树。
3. 对于每个项目(可以按照从下往上的顺序)找到其条件模式基(CPB,conditional patten base),递归调用树结构,删除小于最小支持度的项。如果最终呈现单一路径的树结构,则直接列举所有组合;非单一路径的则继续调用树结构,直到形成单一路径即可。
3.2 FP-growth例题
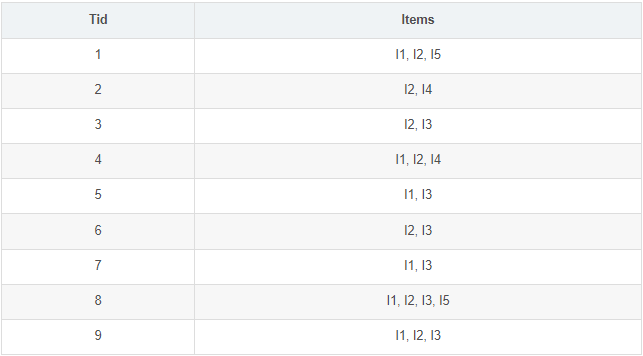
第一步:构建FP树
1. 扫描数据集,对每个物品进行计数:

2. 设置最小支持度(即物品最少出现的次数)为2
3. 按降序重新排列物品集(如果出现计数小于2的物品则需删除)

4. 根据项目(物品)出现的次数重新调整物品清单

5. 构建FP树,加入第一条清单(I2, I1, I5)
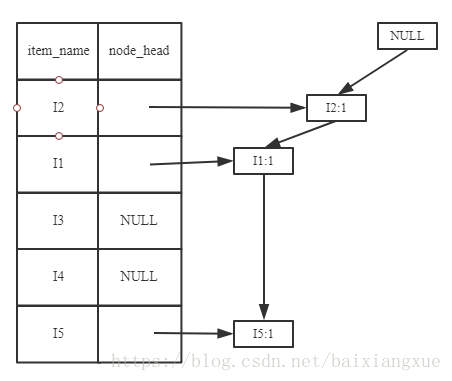
加入第二条清单(I2, I4),出现相同的节点进行累加(I2)

下面一次加入第3~9清单,得到FP树
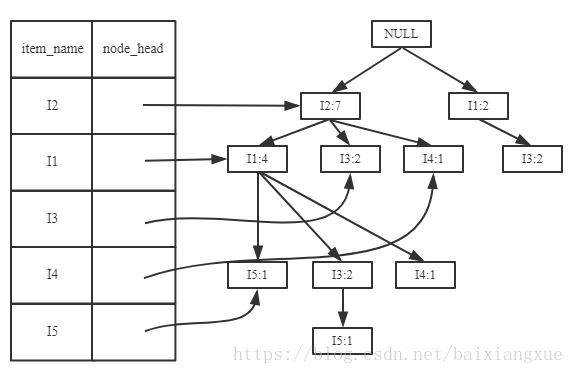
第二步:挖掘频繁项集
对于每一个元素项,获取其对应的条件模式基(cpb)。条件模式基是以所查找元素项未结尾的路劲集合。每一条路劲其实都是一条前缀路劲。
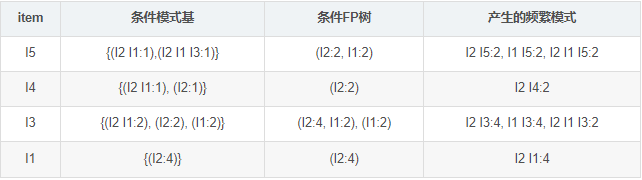
(1)考虑I5,得到条件模式基{(I2 I1 : 1), (I2 I1 I3)},构造条件FP树如下,然后递归调用FP-growth,模式后缀未I5。这个条件FP树是但路劲的,在FP-growth中直接举例{I2:2,I1:2,I3:1}的所有组合,之后和模式后缀I5取并集得到支持度大于2的所有模式:{ I2 I5:2, I1 I5:2, I2 I1 I5:2}。
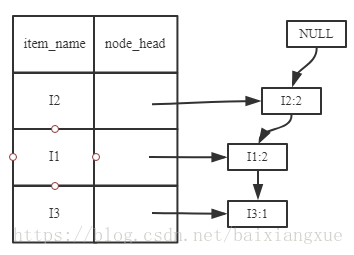
(2)I5的情况是比较简单的,因为I5对应的条件FP-树是单路径的。下面考虑I3,I3的条件模式基是{(I2 I1:2), (I2:2), (I1:2)},生成的条件FP-树如左下图,然后递归调用FP-growth,模式前缀为I3。I3的条件FP-树仍然是一个多路径树,首先把模式后缀I3和条件FP树中的项头表中的每一项取并集,得到一组模式{I2 I3:4, I1 I3:4},但是这一组模式不是后缀为I3的所有模式。还需要递归调用FP-growth,模式后缀为{I1,I3},{I1,I3}的条件模式基为{I2:2},其生成的条件FP-树如右下图所示。这是一个单路径的条件FP-树,在FP-growth中把I2和模式后缀{I1,I3}取并得到模式{I1 I2 I3:2}。理论上还应该计算一下模式后缀为{I2,I3}的模式集,但是{I2,I3}的条件模式基为空,递归调用结束。最终模式后缀I3的支持度大于2的所有模式为:{ I2 I3:4, I1 I3:4, I1 I2 I3:2}
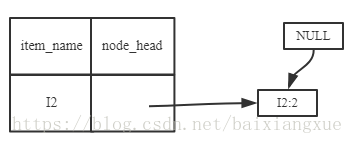
根据FP-growth算法,最终得到的支持度大于2频繁模式如下: