[LOJ#2305]「NOI2017」游戏
[LOJ#2305]「NOI2017」游戏
试题描述
小 L 计划进行 \(n\) 场游戏,每场游戏使用一张地图,小 L 会选择一辆车在该地图上完成游戏。
小 L 的赛车有三辆,分别用大写字母 \(A\)、\(B\)、\(C\) 表示。地图一共有四种,分别用小写字母 \(x\)、\(a\)、\(b\)、\(c\) 表示。
其中,赛车 \(A\) 不适合在地图 \(a\) 上使用,赛车 \(B\) 不适合在地图 \(b\) 上使用,赛车 \(C\) 不适合在地图 \(c\) 上使用,而地图 \(x\) 则适合所有赛车参加。
适合所有赛车参加的地图并不多见,最多只会有 \(d\) 张。
\(n\) 场游戏的地图可以用一个小写字母组成的字符串描述。例如:\(S = \texttt{xaabxcbc}\) 表示小 L 计划进行 \(8\) 场游戏,其中第 \(1\) 场和第 \(5\) 场的地图类型是 \(x\),适合所有赛车,第 \(2\) 场和第 \(3\) 场的地图是 \(a\),不适合赛车 \(A\),第 \(4\) 场和第 \(7\) 场的地图是 \(b\),不适合赛车 \(B\),第 \(6\) 场和第 \(8\) 场的地图是 \(c\),不适合赛车 \(C\)。
小 L 对游戏有一些特殊的要求,这些要求可以用四元组 \((i, h_i, j, h_j)\) 来描述,表示若在第 \(i\) 场使用型号为 \(h_i\) 的车子,则第 \(j\) 场游戏要使用型号为 \(h_j\) 的车子。
你能帮小 L 选择每场游戏使用的赛车吗?如果有多种方案,输出任意一种方案。
如果无解,输出 -1。
输入
输入第一行包含两个非负整数 \(n\), \(d\)。
输入第二行为一个字符串 \(S\)。
\(n\), \(d\), \(S\) 的含义见题目描述,其中 \(S\) 包含 \(n\) 个字符,且其中恰好 \(d\) 个为小写字母 \(x\)。
输入第三行为一个正整数 \(m\),表示有 \(m\) 条用车规则。
接下来 \(m\) 行,每行包含一个四元组 \(i,h_i,j,h_j\),其中 \(i,j\) 为整数,\(h_i,h_j\) 为字符 \(A\) 、\(B\) 或 \(C\),含义见题目描述。
输出
输出一行。
若无解输出 -1。
输入示例
3 1
xcc
1
1 A 2 B
输出示例
ABA
数据规模及约定
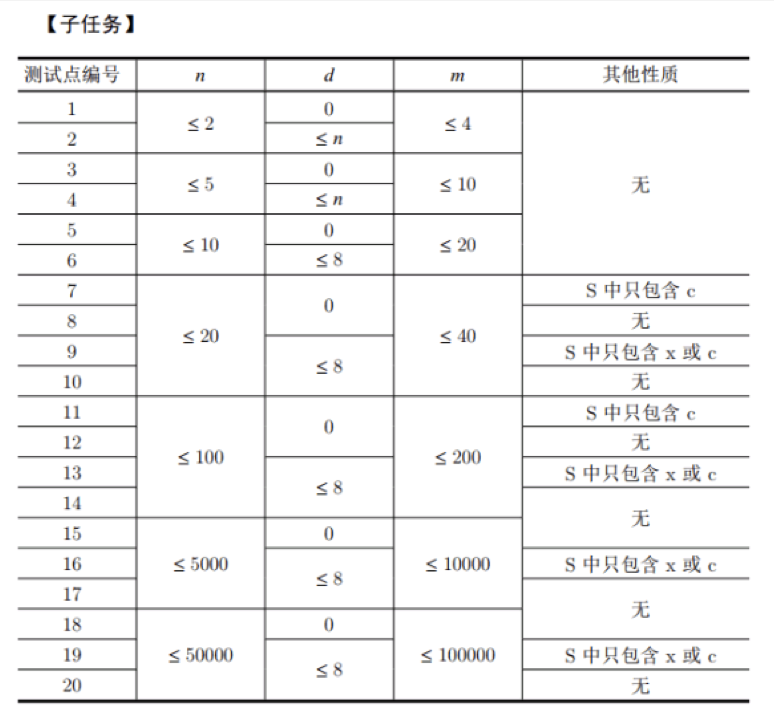
题解
枚举那 \(d\) 个 \(x\) 的地图用 \(A\) 还是用 \(\{ B, C \}\),变成 2-SAT 模型。
#include <bits/stdc++.h>
using namespace std;
#define rep(i, s, t) for(int i = (s), mi = (t); i <= mi; i++)
#define dwn(i, s, t) for(int i = (s), mi = (t); i >= mi; i--)
int read() {
int x = 0, f = 1; char c = getchar();
while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
return x * f;
}
#define maxn 100010
#define maxm 200010
char Map[maxn], Ans[maxn];
int n, m, D, Did[maxn], CntP;
struct Clause {
int a, ta, b, tb;
Clause() {}
Clause(int _1, int _2, int _3, int _4): a(_1), ta(_2), b(_3), tb(_4) {}
} cs[maxm];
bool NeverHappen(int a, int ta, int s) {
if(Map[a] == ta + 'a') return 1;
if(ta && Map[a] == 'x' && (s >> Did[a] & 1)) return 1;
if(!ta && Map[a] == 'x' && !(s >> Did[a] & 1)) return 1;
return 0;
}
struct Point {
int id;
Point(): id(0) {}
int p() { return id ? id : id = ++CntP; }
} use[maxn][3];
int sumTp[maxn];
namespace G {
int m, head[maxn], nxt[maxm], to[maxm];
void clear() {
m = 0; memset(head, 0, sizeof(head));
return ;
}
void AddEdge(int a, int b) {
to[++m] = b; nxt[m] = head[a]; head[a] = m;
return ;
}
int dfn[maxn], low[maxn], clo, scno[maxn], cnts, S[maxn], top;
void init() {
memset(dfn, 0, sizeof(dfn));
memset(low, 0, sizeof(low));
clo = 0;
memset(scno, 0, sizeof(scno));
cnts = 0;
return ;
}
void dfs(int u) {
dfn[u] = low[u] = ++clo;
S[++top] = u;
for(int e = head[u]; e; e = nxt[e]) {
if(scno[to[e]]) continue;
if(dfn[to[e]]) low[u] = min(low[u], dfn[to[e]]);
else dfs(to[e]), low[u] = min(low[u], low[to[e]]);
}
if(low[u] == dfn[u]) {
cnts++;
while(S[top] != u) scno[S[top--]] = cnts;
scno[S[top--]] = cnts;
}
return ;
}
}
int main() {
n = read(); D = read();
scanf("%s", Map + 1);
m = read();
rep(i, 1, m) {
int a = read(), b;
char cha[5], chb[5];
scanf("%s", cha);
b = read();
scanf("%s", chb);
cs[i] = Clause(a, cha[0] - 'A', b, chb[0] - 'A');
}
int cD = 0;
rep(i, 1, n) if(Map[i] == 'x') Did[i] = cD++;
int all = (1 << D) - 1;
rep(s, 0, all) {
CntP = 0;
memset(use, 0, sizeof(use));
G::clear();
rep(i, 1, n) if(Map[i] != 'x') {
if(Map[i] == 'a') use[i][1].p(), use[i][2].p(), sumTp[i] = 3;
if(Map[i] == 'b') use[i][0].p(), use[i][2].p(), sumTp[i] = 2;
if(Map[i] == 'c') use[i][0].p(), use[i][1].p(), sumTp[i] = 1;
}
else {
if(s >> Did[i] & 1) G::AddEdge(use[i][1].p(), use[i][0].p()), sumTp[i] = 1;
else use[i][1].p(), use[i][2].p(), sumTp[i] = 3;
}
rep(i, 1, m) {
if(NeverHappen(cs[i].a, cs[i].ta, s)) continue;
if(NeverHappen(cs[i].b, cs[i].tb, s)) G::AddEdge(use[cs[i].a][cs[i].ta].p(), use[cs[i].a][sumTp[cs[i].a]-cs[i].ta].p());
else
G::AddEdge(use[cs[i].a][cs[i].ta].p(), use[cs[i].b][cs[i].tb].p()),
G::AddEdge(use[cs[i].b][sumTp[cs[i].b]-cs[i].tb].p(), use[cs[i].a][sumTp[cs[i].a]-cs[i].ta].p());
}
G::init();
rep(i, 1, CntP) if(!G::dfn[i]) G::dfs(i);
bool ok = 1;
rep(i, 1, n) {
if(sumTp[i] == 3) {
if(G::scno[use[i][1].p()] == G::scno[use[i][2].p()]) { ok = 0; break; }
else Ans[i] = G::scno[use[i][1].p()] < G::scno[use[i][2].p()] ? 'B' : 'C';
}
if(sumTp[i] == 2) {
if(G::scno[use[i][0].p()] == G::scno[use[i][2].p()]) { ok = 0; break; }
else Ans[i] = G::scno[use[i][0].p()] < G::scno[use[i][2].p()] ? 'A' : 'C';
}
if(sumTp[i] == 1) {
if(G::scno[use[i][0].p()] == G::scno[use[i][1].p()]) { ok = 0; break; }
else Ans[i] = G::scno[use[i][0].p()] < G::scno[use[i][1].p()] ? 'A' : 'B';
}
}
if(ok) return Ans[n+1] = 0, puts(Ans + 1), 0;
}
puts("-1");
return 0;
}



