[LOJ#2323]「清华集训 2017」小Y和地铁

[LOJ#2323]「清华集训 2017」小Y和地铁

试题描述

小Y是一个爱好旅行的OIer。一天，她来到了一个新的城市。由于不熟悉那里的交通系统，她选择了坐地铁。

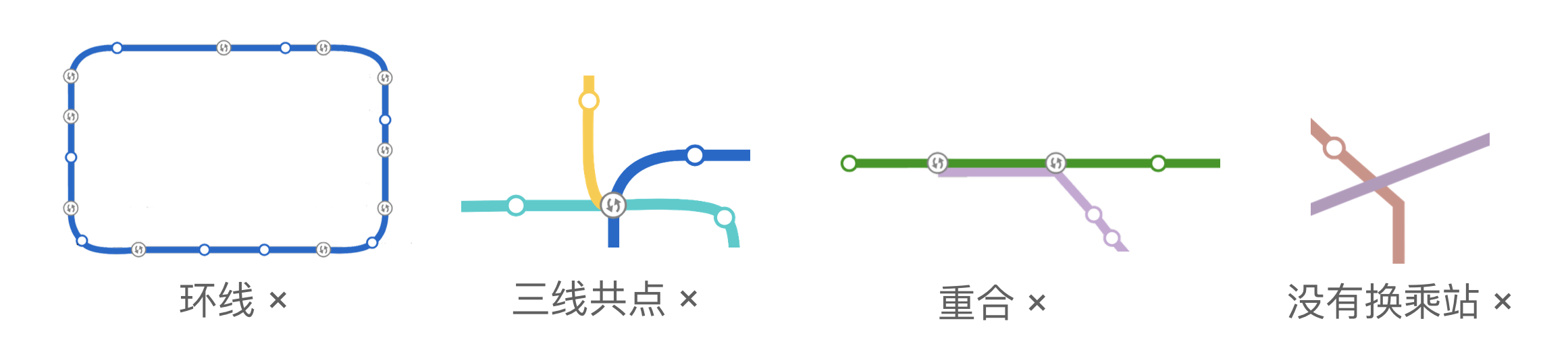
她发现每条地铁线路可以看成平面上的一条曲线，不同线路的交点处一定会设有换乘站。通过调查得知，没有线路是环线，也没有线路与自身相交。任意两条不同的线路只会在若干个点上相交，没有重合的部分，且没有三线共点的情况。即，如图所示的情况都是不存在的：

小Y坐着地铁 \(0\) 号线，路上依次经过了 \(n\) 个换乘站。她记下了每个换乘站可以换乘的线路编号，发现每条线路与她所乘坐的线路最多只有 \(2\) 个换乘站。现在小Y想知道，除掉她经过的换乘站以外，这个城市里最少有几个换乘站。只有你告诉她正确的答案，她才会答应下次带你去玩呢。

输入

请注意本题有多组输入数据。

输入数据的第一行是一个整数 \(T\)，表示输入数据的组数。接下来依次给出每组数据。

对于每组数据，第一行是一个整数 \(n\)，表示小Y经过的换乘站的数目。第二行为 \(n\) 个用空格隔开的整数，依次表示每个换乘站的可以换乘的线路编号。这些编号都在 \(1\) ~ \(n\) 之内。

输出

对于每组输入数据，输出一行一个整数，表示除掉这 \(n\) 个换乘站之外，最少有几个换乘站。

输入示例

4
4
1 2 1 2
8
1 2 3 4 1 2 3 4
5
5 4 3 3 5
8
1 2 3 4 1 3 2 4

输出示例

0
0
0
1

数据规模及约定

对于所有测试点，以及对于样例，\(1 \le T \le 100, 1 \le n \le 44\)。

题解

我们需要先意识到一个性质，下面这两张图是等价（即对于任意一种方案，把其中的一个换成另一个，交点数不会变）的：

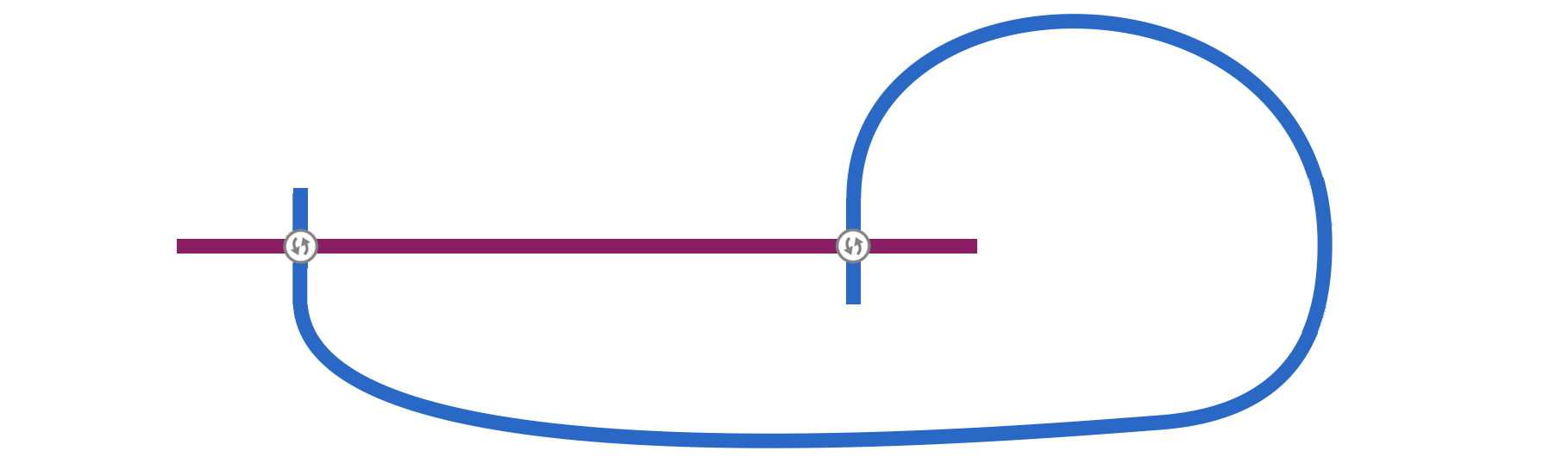
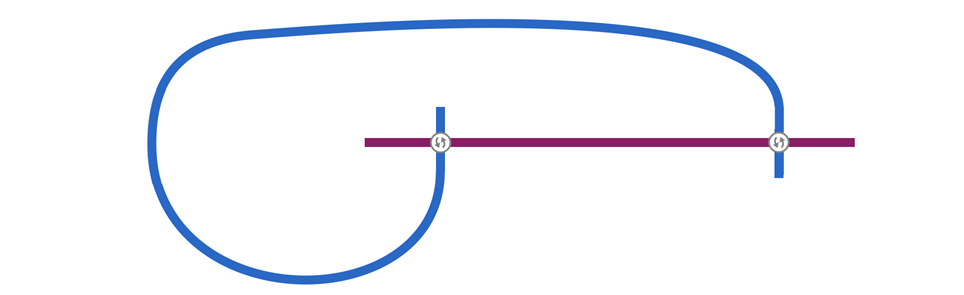
我们发现两条路线等价当且仅当左右两端点向下或向上方向都一致。

于是这题就可以暴搜了，忽略所有只有一个交点的转站，剩下的按左端点排序然后 dfs，维护一下当前右端点朝上和朝下连出去的接头的信息，用个树状数组就好了。

mdzz 这题居然是暴搜

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
using namespace std;
#define rep(i, s, t) for(int i = (s); i <= (t); i++)
#define dwn(i, s, t) for(int i = (s); i >= (t); i--)

int read() {
	int x = 0, f = 1; char c = getchar();
	while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
	while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
	return x * f;
}

#define maxn 50
#define oo 2147483647

int n, A[maxn], cnt, l[maxn], r[maxn];

struct Data {
	int C[maxn];
	void add(int x, int v) {
		for(; x <= n; x += x & -x) C[x] += v;
		return ;
	}
	int sum(int x) {
		int ans = 0;
		for(; x; x -= x & -x) ans += C[x];
		return ans;
	}
	int que(int l, int r) {
		if(l > r) return 0;
		return sum(r) - sum(l - 1);
	}
} up, dwn;

int ans;
void dfs(int now, int nans) {
	if(nans >= ans) return ;
	if(now > cnt) return (void)(ans = nans);
	up.add(r[now], 1);
	dfs(now + 1, nans + min(up.que(l[now], r[now] - 1), up.que(r[now] + 1, n) + dwn.que(l[now], n)));
	up.add(r[now], -1);
	dwn.add(r[now], 1);
	dfs(now + 1, nans + min(dwn.que(l[now], r[now] - 1), dwn.que(r[now] + 1, n) + up.que(l[now], n)));
	dwn.add(r[now], -1);
	return ;
}

int main() {
	int T = read();
	
	while(T--) {
		n = read();
		rep(i, 1, n) A[i] = read();
		
		cnt = 0;
		rep(i, 1, n) rep(j, i + 1, n) if(A[j] == A[i]) l[++cnt] = i, r[cnt] = j;
		
		ans = oo;
		dfs(1, 0);
		printf("%d\n", ans);
	}
	
	return 0;
}