P1063 能量项链 区间DP

题干 AC记录

我原本的dfs的转移式子就只有将两边的单个拎出来，将其余的大基团合并

也就是这两个情况：

 和

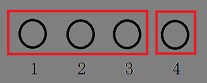
但是忽视了类似这种的情况：

也就是说，我没有讨论两个大基团合并的情况，只讨论了单点跟基团合并

后来开始使用区间DP的套路

然而出现了如下这些问题：

---

先上个AC代码，其中有死亡处被我用括号括起来了

#include<iostream>
#include<cstdio>
#define NUM 510
#define int long long
#define FOR(a,b,c) for( int a = b;a <= c;a++ )
using namespace std;

int n;
int a[NUM];
long long dp[NUM][NUM];

signed main(){
    
    cin >> n;
    FOR( i,1,n ){
        cin >> a[i];
        a[i+n] = a[i];
    }
    
    FOR( len,2,n+2 ){ //枚举区间长度(n+1)
        FOR( l,1,n*2-len+1 ){ //( 循环条件改了，原来是枚举到n )
            int r = l+len-1;
            
//          if( len == 2 ){ //( 删除掉！ )
//              dp[l][r] = a[l]*a[r]*a[r+1];
//              printf( "区间为%d-%d，dp = %d\n",l,r,dp[l][r] );
//              continue;
//         }
            FOR( t,l+1,r-1 ){
                dp[l][r] = max( dp[l][r],dp[l][t]+dp[t][r]+a[l]*a[t]*a[r] );//(*a[t]*a[r])
            }
//          printf( "区间为%d-%d，dp = %d\n",l,r,dp[l][r] );
        }
    }
    long long ans = 0;
    FOR( i,1,n ){
        ans = max( ans,dp[i][i+n] );//( [i+n] )
    }
    cout << ans;
    
    return 0;
}

1. 不要特判长度为$2$，直接让长度$3$的去作为最小的区间，甚至可以不要长度为2的更新

2. 答案为dp[i][i+n]，因为是个环，所以要有$n+1$个数

3. 如2，区间长度也要是$n+1$

4. 枚举起点要枚举到$n*2-len+1$，因为不同的区间长度，不能都是枚举到$n$是吧(xjj)

5. 理解问题了就是，转移方程应该是由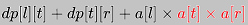转移得到