Johnson 全源最短路
直接照搬了，部分删减
Johnson 和 Floyd 一样，是一种能求出无负环图上任意两点间最短路径的算法。
1 算法概述
任意两点间的最短路可以通过枚举起点，跑 n 次 Bellman-Ford 算法解决，时间复杂度是$O(n^2m) $的，也可以直接用 Floyd 算法解决，时间复杂度为 $ O(n^2m) $。
注意到堆优化的 Dijkstra 算法求单源最短路径的时间复杂度比 Bellman-Ford 更优，如果枚举起点，跑n次Dijkstra算法，就可以在（本文中的Dijkstra采用 priority_queue 实现，下同）的时间复杂度内解决本问题，比上述跑 $n$ 次 Bellman-Ford 算法的时间复杂度更优秀，在稀疏图上也比 Floyd 算法的时间复杂度更加优秀。
但 Dijkstra 算法不能正确求解带负权边的最短路，因此我们需要对原图上的边进行预处理，确保所有边的边权均非负。
Johnson 算法则通过另外一种方法来给每条边重新标注边权。
我们新建一个虚拟节点（在这里我们就设它的编号为 0 ）。从这个点向其他所有点连一条边权为 0 的边。
接下来用 Bellman-Ford 算法求出从0号点到其他所有点的最短路，记为 。
假如存在一条u点到v点，边权为w的边，则我们将该边的边权重新设置为
接下来以每个点为起点，跑 n轮 Dijkstra 算法即可求出任意两点间的最短路了。
容易看出，该算法的时间复杂度是
Q：那这么说，Dijkstra 也可以求出负权图（无负环）的单源最短路径了？
A：没错。但是预处理要跑一遍 Bellman-Ford，还不如直接用 Bellman-Ford 呢。
2 正确性证明
为什么这样重新标注边权的方式是正确的呢？
在讨论这个问题之前，我们先讨论一个物理概念——势能。
诸如重力势能，电势能这样的势能都有一个特点，势能的变化量只和起点和终点的相对位置有关，而与起点到终点所走的路径无关。
势能还有一个特点，势能的绝对值往往取决于设置的零势能点，但无论将零势能点设置在哪里，两点间势能的差值是一定的。
接下来回到正题。
在重新标记后的图上,从s点到t点的一条路径的长度表达式如下：
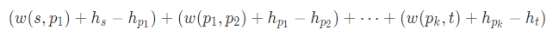
化简后得到：
无论我们从 s到 t走的是哪一条路径，的值是不变的，这正与势能的性质相吻合！
为了方便，下面我们就把$h_i$称为$i$点的势能。
上面的新图中s$\to$t的最短路的长度表达式由两部分组成，前面的边权和为原图中s→t 的最短路，后面则是两点间的势能差。因为两点间势能的差为定值，因此原图上s$\to$t 的最短路与新图上s$\to$t的最短路相对应。
到这里我们的正确性证明已经解决了一半——我们证明了重新标注边权后图上的最短路径仍然是原来的最短路径。接下来我们需要证明新图中所有边的边权非负，因为在非负权图上，Dijkstra 算法能够保证得出正确的结果。
根据三角形不等式，新图上任意一边 (u,v)上两点满足：。这条边重新标记后的边权为 。这样我们证明了新图上的边权均非负。
至此，我们就证明了 Johnson 算法的正确性。
3 代码
//Johnson全源 #include<iostream> #include<cstdio> #include<queue> #include<cstring> #define NUM 3010 #define INF 1e9 //9个0,1e9 #define FOR(a,b,c) for( int a = b;a <= c;a++ ) using namespace std; int n,m; struct bian{ int next,to; long long w; }; bian e[NUM<<3]; struct dian{ int id,dis;//点的编号，该点到目标点的距离 bool operator < (const dian &x) const{ return dis > x.dis;//小根堆 } dian( int x,int y ){ dis = x;id = y;//先距离后编号 } }; int head[NUM]; int t[NUM];//被更新的次数 long long h[NUM]; long long d[NUM];//点的距离 bool v[NUM]; int cnt; void add( int x,int y,long long w ){ e[++cnt].next = head[x]; e[cnt].to = y; e[cnt].w = w; head[x] = cnt; } bool spfa(){ //spfa求个单源最短路 queue <int> q; memset( h,63,sizeof(h) );//设置为最大值，玄学memset q.push(0); h[0] = 0;v[0] = 1; while( !q.empty() ){ int hao = q.front();//这个边的起点 q.pop();v[hao] = 0;//出队 for( int i = head[hao];i;i = e[i].next ){ int to = e[i].to; if( h[to] <= h[hao] + e[i].w ) continue;//无需更新 h[to] = h[hao] + e[i].w;//更新路程 if( v[to] ) continue;//已经在栈里了，就不管了 q.push(to);v[to] = 1;//入栈 t[to]++;//更新，为了判断负环 if( t[to] >= n+1 ) return 1;//存在负环 } } return 0; } void dij( int s ){ //普通的迪杰堆优化 priority_queue <dian> q; FOR( i,1,n ) //初始化 d[i] = INF; memset( v,0,sizeof(v) );//重复使用一下v数组 d[s] = 0; q.push( dian(0,s) );//放入起点 while( !q.empty() ){ int hao = q.top().id;//最近的点的编号 q.pop(); if( v[hao] ) continue; v[hao] = 1;//这个点已经作为了更新点 for( int i = head[hao];i;i = e[i].next ){ int to = e[i].to; if( d[to] > d[hao] + e[i].w ){ d[to] = d[hao] + e[i].w; if( v[to] ) continue;//放到下面来！ q.push( dian( d[to],to ) );//放入终点 } } } } int main(){ cin >> n >> m; FOR( i,1,m ){ int x,y,w; cin >> x >> y >> w; add( x,y,w ); } FOR( i,1,n ) add( 0,i,0 ); if( spfa() ){ cout << -1; return 0; } FOR( x,1,n ) for( int i = head[x];i;i = e[i].next ) e[i].w += h[x] - h[e[i].to];//令边权都非负 FOR( i,1,n ){ dij( i ); long long ans = 0; FOR( j,1,n ){ if( i == j ) continue; if( d[j] == INF ) ans += j * INF; else ans += j * ( d[j] + h[j] - h[i] ); } cout << ans << endl; } return 0; }
4 第一次敲板子出现的问题
1. 没输入m,边是按照n输入的....
2. 没在dij取堆顶的时候判断这个点是不是已经被访问过了
3. 学了个构造函数(也许？)
4. 没开long long
5. 边的数组开小了！！！
