tarjan

终于来到了差点让我破防的tarjan

争取说明白吧

定义：

1. 桥：指去掉该边，其原本所在的强连通分量变为两部分（即不再是强连通分量）

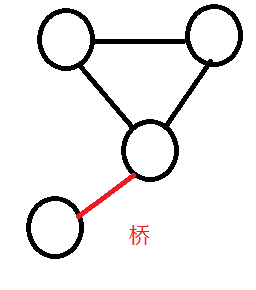
2. 边双连通分量：即没有桥的无向连通图

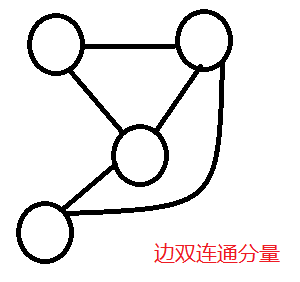
3. 强连通分量：即没有桥的有向连通图

 

求无向图的边双连通分量的数量

---

我们的思路是，从某一节点作为根节点开始dfs遍历图，使用一个$dfn$记录该节点的$dfs$序

再用一个$low$，记录这个点可以往上跑，跑到的最高的点的$dfn$的值

显然，如果$dfn[i] > low[i]$，则说明该节点可以查到自己的祖先，记作种类2

那如果$dfn[i] = low[i]$ ，就说明这个点就是所在连通分量的最上面一个点，记作种类1

我们开一个栈，然后访问到一个点就把这个点压入栈中

对于种类2，必然在栈中位于种类1的前面（因为后遍历到）

所以一旦发现点p为种类1，直接弹栈至p，其中弹出的所有元素都跟p在一个强连通分量里

代码如下：

#include<iostream>
#include<cstdio>
#include<stack>
#define NUM 1010
#define FOR(a,b,c) for( int a = b;a <= c;a++ )
using namespace std;

int n;
int a[NUM];
struct bian{
    int next,to;
};
bian e[NUM];
int head[NUM];
int dfn[NUM],low[NUM];
int id[NUM];
int cnt,scc;

void add( int x,int y ){
    e[++cnt].next = head[x];
    e[cnt].to = y;
    head[x] = cnt;
}
int timess;
stack <int> st;
bool ins[NUM];//判断这个点是不是已经在栈里了
void tarjan( int p ){
    dfn[p] = ++timess;
    low[p] = timess;//更新时间戳
    st.push( p );ins[p] = 1;//将该点压入栈中
    for( int i = head[p];i;i = e[i].next ){
        int to = e[i].to;
        if( !dfn[to] ){ //如果终点没有访问过
            tarjan( to );
            low[p] = min( low[p],low[to] );
        }else if( ins[to] ) //已经在栈里说明之前已经访问过，是之前的点
            low[p] = min( dfn[to],low[p] ); 
    }
    if( dfn[p] == low[p] ){ //以下是一个独立的强连通分量
        ++scc;//分量数++
        int hao;//栈顶点编号
        do{
            hao = st.top();
            st.pop();
            id[hao] = scc;//该点所在的分量编号
        }while( hao != p );//从栈顶到该点是一个连通分量
    }  
}
int m;
int main(){
    
    cin >> n >> m;
    FOR( i,1,m ){ //边数
        int x,y;
        cin >> x >> y;
        add( x,y );//有向边
    }
    
    FOR( i,1,n )
        if( !dfn[i] )
            tarjan( i );

    cout << "\n\n";

    FOR( i,1,n ) //输出每个点所在的连通块编号
        cout << i << " " << id[i] << "\n";
    
    return 0;
}

 

边双连通分量

 

 

---