威尔逊定理
一、定理内容
当$p$为质数的时候,$(p-1)+1$可以被$p$整除,
也就是$(p-1)!+1$ $\equiv 0$ $(mod$ $p$),即$(p-1)! \equiv -1 \pmod{p} $
该条件为$p$为质数的充分必要条件
二、证明

当p为完全平方数时:
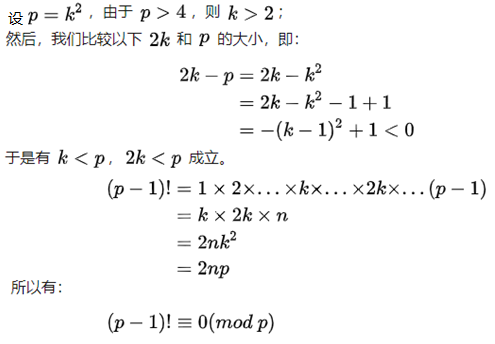
当p不是完全平方数时:

三、应用
例一:
给定一个正整数$n$,求$n-1)! mod n$的值。
数据范围:$2<=n<=1e9$

考虑n为质数与不为质数两种情况: 当 n 为素数时,这个就是威尔逊定理,答案为n-1; 当n不为素数时,我们在证明威尔逊定理的充分性时,已经对它进行了一个分类: 当n=4时,结果为 2; 否则,可以根据 完全平方数 和 非完全平方数,均得到结果为 0。
例二:
给定$n$的值,用下面的公式求$S_n$,公式中的[ ]指的是向下取整。
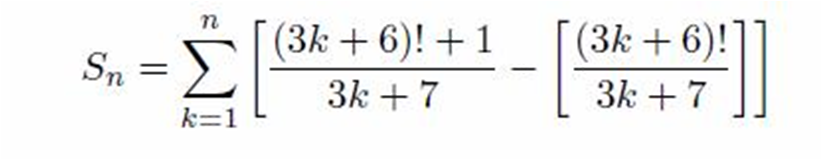
数据范围:$t<=1e6,1<=n<=1e6$
————————————————————
解:
看到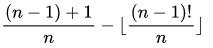 的形式,就应该联想到威尔逊定理
的形式,就应该联想到威尔逊定理
根据$3k+7$的性质分别计算
当$3k+7$为质数,根据威尔逊定理得: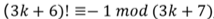 ,即$(3k+6)!+1$可以被$3k+7$整除
,即$(3k+6)!+1$可以被$3k+7$整除
设$\frac{(3k+6)!+1}{3k+7} = x$,则原式为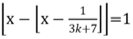 (
(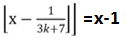 )
)
当$3k+7$不是质数时,$k>=1$,所以$3k+7>4$,根据威尔逊定理的证明得,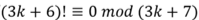 ,即$\frac{(3k+6)!}{3k+7}$一定为整数
,即$\frac{(3k+6)!}{3k+7}$一定为整数
设$\frac{(3k+6)!}{3k+7} = x$,则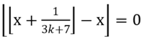
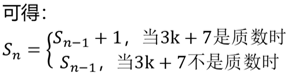




 浙公网安备 33010602011771号
浙公网安备 33010602011771号