扩展欧几里得

解决的问题描述：

---

对于三个自然数$a,b,c$，求解$ax + by = c$的$(x,y)$的整数解

算法解决：

---

 首先我们要判断是否存在解，对于这个这个存在整数解的充分条件是$gcd(a,b)$  $|$ $ c$

也就是说$c$为$gcd(a,b)$的一个倍数

然后判定是否有解后，我们需要在这个基础上求一组解(x,y)

由于 $a,b,c$ 都是 $gcd(a,b)$ 的倍数

我们将它们都除以 $gcd(a,b)$ ，不影响后面的计算

这时问题就变成了求对于$ax + by = 1 $ 且 $a,b$ 互质时，$(x,y)$ 的解

对于a,b有负数的情况，我们需要将他们其中一个负数加上另外一个数直到非负。

（由于前面朴素欧几里得定理是不会影响的）

如果a,b是两个负数，直接将整个式子反号，然后放到 c上就行了

下面推一波式子：

　　$ax + by = gcd(a,b) = 1$

　　　　　  $= gcd(b,a$%$b)$（辗转相除）

　　　　　$\Rightarrow bx + (a$ % $b)y$（转化一下）

　　　　　  $= bx + (a - \left \lfloor \frac{a}{b} \right \rfloor b ) y$

　　　　　  $= bx + ay - \left \lfloor \frac{a}{b} \right \rfloor by$

　　　　　  $= ay + b( x - \left \lfloor \frac{a}{b} \right \rfloor y )$

 不难发现此时$a$的系数$x$变成了$y$，而$y$变成了$x - \left \lfloor \frac{a}{b} \right \rfloor y$，利用这个性质，我们可以递归求解$(x,y)$

递归的边界其实跟辗转相除一样（$b == 0$时退出），此时因为$b = 0$，所以$a = 1,ax + by = 1$，其中的解为$x = 1,y = 0$

作为这些我们就可以在$O(log)$的时间内得到了一组$(x,y)$的特殊解

解系扩展(哈？)

---

但常常我们要求对于$x or y$ 的最小非负整数解，这个的话我们需要将单个$(x,y)$扩展成了一个解系

如果学过不定方程的话，就可以轻易得到这个解系的，在此不过多赘述了

　　　　　　　　　　

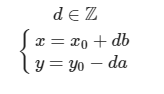
 要记住，(x,y)都要乘上$e$

然后我们直接令$x$为$( x$ % $b ) + b$ % $b$就行了

代码实现

---

 递归调用的话，$y = x',x = y'$，只需要修改$y$就行了

void Exgcd( int a,int b,int &x,int &y ) { //取地址符即直接改变该元素的数值，可以理解为一个全局变量 
    if( !b ){ //如果b = 0 
        x = 1;
        y = 0;
    }else Exgcd( b,a % b,y,x ), y -= a/b*x;
}