行列式与高斯消元基础
一、二元线性方程与二阶行列式
(一)二元线性方程的解
设有方程:
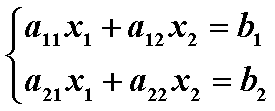

可看出$x_1,x_2$的分母相同,由$x$的四个系数组成
而两数分子由三对系数组合构成
(二)行列式
引进一个符号表示“四个数分成两对相乘再相减”
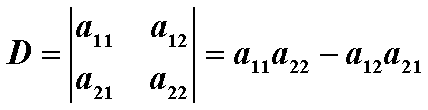
其中,$a_{ij}(i = 1,2 ; j = 1,2)$称为行列式中的元素,且:
i 为行标,表明元素位于第i 行;
j 为列标,表明元素位于第j 列
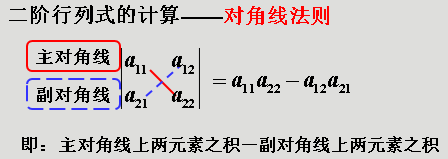
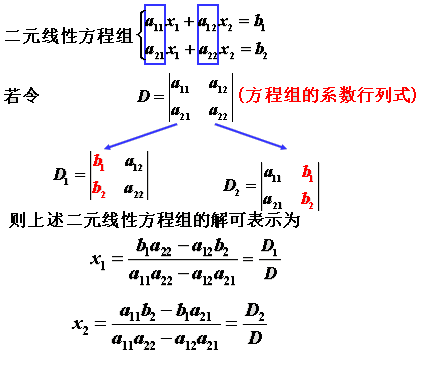

二、排列与逆序
(一)排列
对于$n$个不同的元素,共有$n !$种排列方式,叫做$n$个元素的全排列,用$P_n$表示
而大部分的排列都不是“顺序”(只有一个,为$“1 2 3 \cdot\cdot\cdot (n-1) n”$)
而是逆序
(二)逆序
定义
1. n 个不同的自然数,规定从小到大为标准次序.
2. 当某两个元素的先后次序与标准次序不同时,
就称这两个元素组成一个逆序(可理解为逆序对)
3. 排列中所有逆序的总数称为此排列的逆序数.
排列$i_1 i_2 \cdot\cdot\cdot i_n$的逆序数通常记为$t(i_1 i_2 \cdot\cdot\cdot i_n)$
三、n阶行列式的定义
(一)三阶行列式


并将其简记作$D = det(a_{ij})$,其中$a_{ij}$为行列式$D$的$(i,j)$元
其中,$\sum_{p1p2p3}$表示对$1,2,3$的所有排列求和
二阶行列式也有类似性质,下面将行列式推广到一般情形
(二)$n$阶行列式
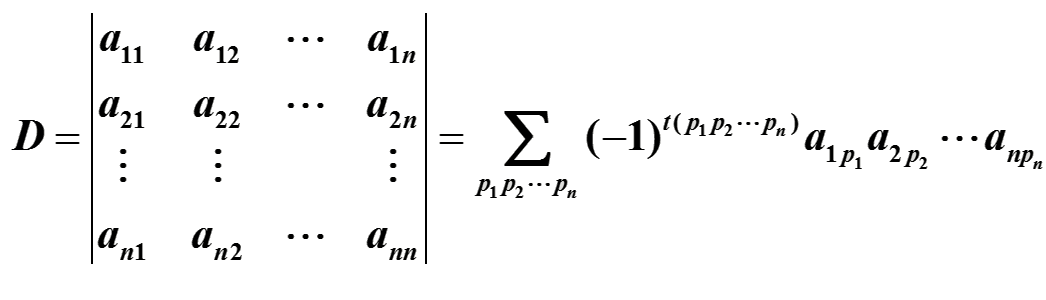
其中:
1.$n$阶行列式有$n !$项
2. 每一项都是位于不同行不同列的$n$个元素的乘积(类似于数独)

例:写出四阶行列式中含有因子$a_11 a_23$的项

因为下标的第一项按照1,2,3,4排列,第二项是1,2,3,4的任一排列 故答案为a_11 a_23 a_32 a_44 或a_11 a_23 a_34 a_42
(四)特殊行列式的计算
对于四阶行列式中:
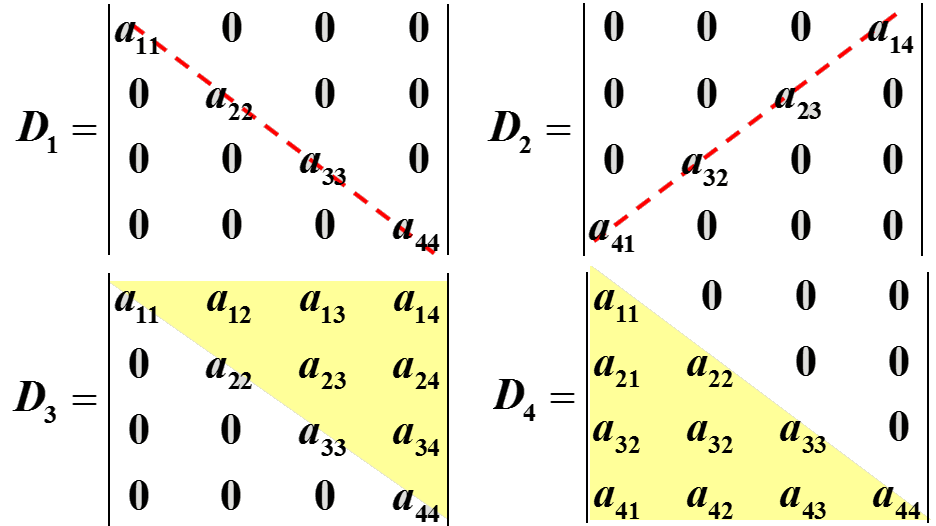
(1) D1 = $a_11a_22a_33a_44$
(2) D2 = $a_14a_23a_32a_41$($t(4 3 2 1) = \frac{3 \times 4}{2} = 6$故取正号)
(3) D3 = $a_11a_22a_33a_44$(其它项数全是$0$)
(4) D4 = $a_11a_22a_33a_44$(其它项数全是$0$)
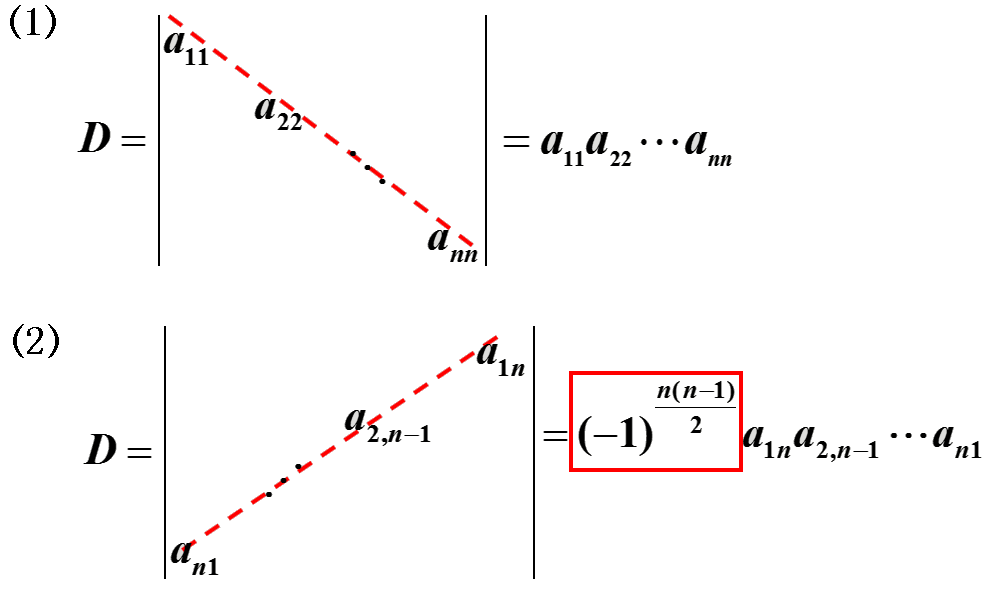
故对于任意$n$阶行列式:
对角行列式:
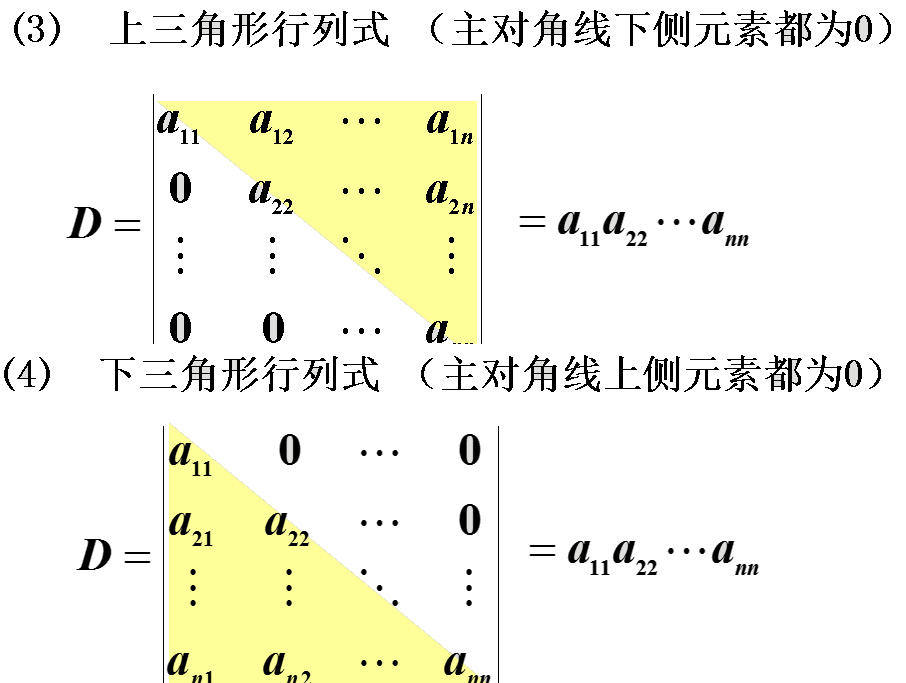
四、行列式的性质
所有对行列式中的行成立的性质对列同样成立
性质1:行列式与其转置行列式数值相等,即$D = det(a_{ij}) = D^T = det(a_{ji})$
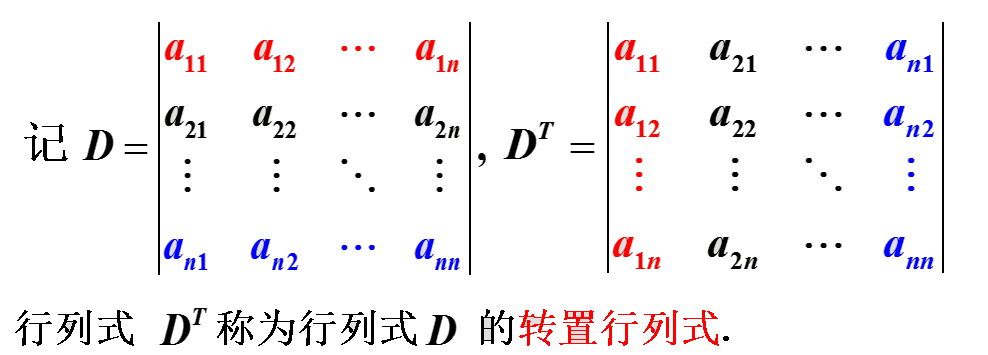
可理解为将$D$与$D^T$沿$y = -x$对称
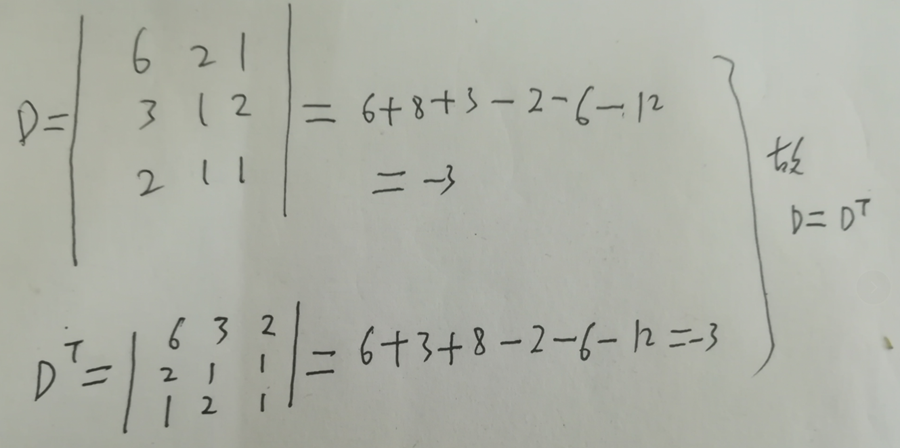
_______________________________________________________________
性质2:互换行列式中的两行(列),行列式变号
其中$r,c$分别表示“行,列”
_______________________________________________________________
性质3:行列式中的某一行(列)中所有元素同乘一个倍数$k$,等于用$k$乘以行列式

_______________________________________________________________
性质4:行列式中如果有两行(列)元素成比例,则此行列式值为$0$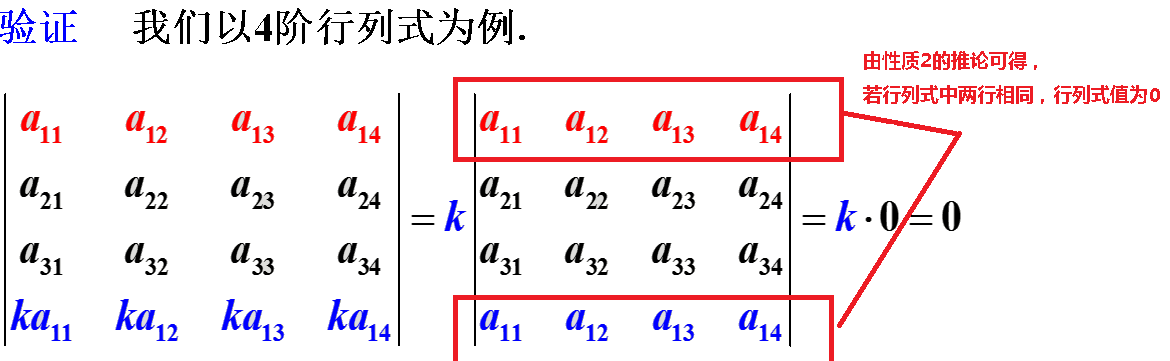
_______________________________________________________________
性质5:若行列式的某一行(列)的元素都是两数之和,则可以将其写作两个行列式的和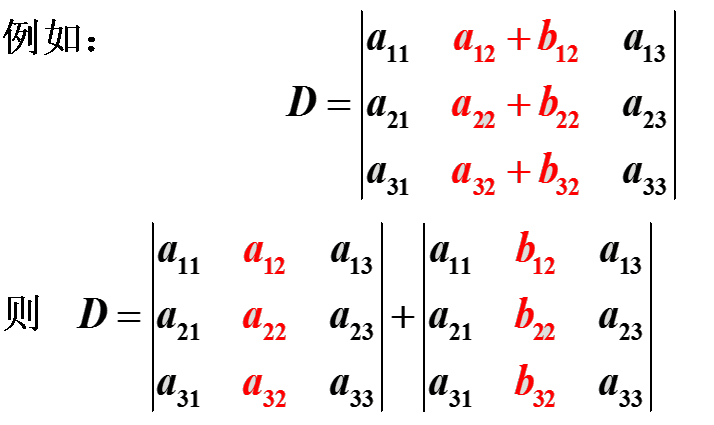
_______________________________________________________________
性质6:把行列式的某一行(列)的每个元素都乘以相同的倍数再加到另一个行(列)的对应元素上,行列式数值不变

_______________________________________________________________
小结

五、高斯消元
高斯消元就是利用行列式的性质将一个行列式消成一个上三角(或下三角)的特殊行列式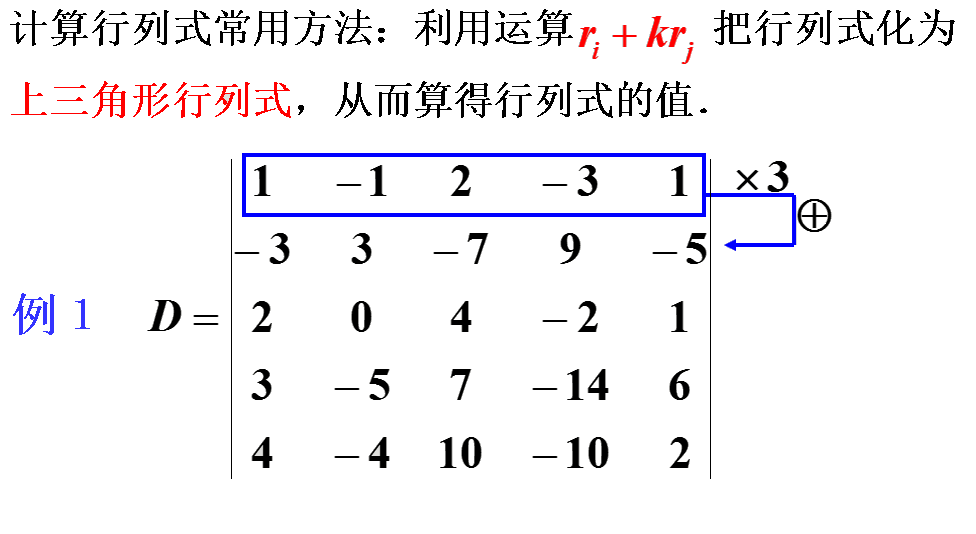

最后就是计算这个上三角的行列式数值即可,即计算其对角线的乘积





