ST表
ST表嘛,就是一个可以解决可重复贡献问题的东西,并且很快,但是不支持修改
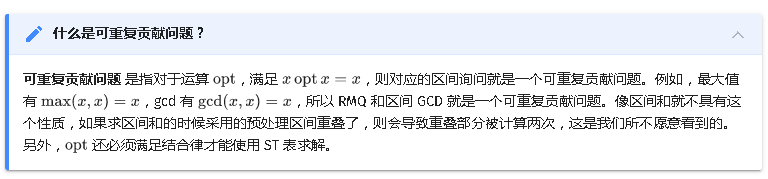
ST 表基于倍增思想,可以做到在$O(n \log_n)$时间内预处理, $O(1)$回答每个询问
实现+原理
先上代码,就着代码讲原理

1 #include <bits/stdc++.h> 2 using namespace std; 3 const int logn = 21; 4 const int maxn = 2000001; 5 int f[maxn][logn+1];//f[i][j]表示从i开始往后j个元素的最大值 6 int Logn[maxn+1];//查找最小的幂次 7 8 void pre(){ // 准备工作,初始化 9 Logn[1] = 0; 10 Logn[2] = 1; 11 for( int i = 3;i < maxn;i++ ){ //预处理所有数字的幂次 12 Logn[i] = Logn[i/2] + 1; 13 } 14 } 15 16 int main(){ 17 int n,m; 18 cin >> n >> m; 19 for( int i = 1;i <= n;i++ ){ 20 cin >> a[i]; 21 f[i][0] = a[i];//2^0=1,故 f[i][0]存的即是a[i] 22 } 23 pre();//预处理对数 24 for( int j = 1;j <= logn;j++ ) 25 for( int i = 1;i+(1<<j)-1 <= n;i++ ) 26 f[i][j] = max( f[i][j-1],f[ i+(1<<(j-1)) ][j-1] ); 27 //预处理ST表 28 for( int i = 1;i <= m;i++ ){ 29 int x,y; 30 cin >> x >> y; 31 int s = Logn[y-x+1]; 32 cout << max( f[x][s],f[ y-(1<<s)+1 ][s] ); 33 } 34 return 0; 35 }
原数组:

如果找$a[1-6]$的最大值的话,则有$x = 1,y = 6$,根据代码的第$31$行可得,$s = Logn[6-1+1] = 2$
于是我们可以将整个数列分为$a[1-4]$与$a[3-6]$两个部分,其中每个部分都是有$Logn[6]^2 = 2^2 = 4$个数
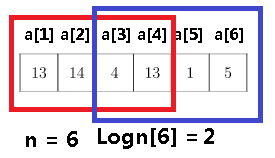
其中第32行的$f[x][s]$就是对应上图的$f[1][2]$
$y-(1<<s)+1 = 6-(1<<2)+1 = 7 - 4 = 3$
所以$f[ y-(1<<s)+1 ][s]$就是对应的$f[3][2]$
第32行的意思就是取这两个部分各自最大值的最大值
例题





