归并排序

归并排序是利用了分治，在$O( n \log_n )$的时间里完成排序

虽然它比$sort$难打，但是它稳定还快啊（快排的最劣复杂度为$O( n^2 )$，而归并的最劣复杂度还是$O( n \log_n )$）

 

原理

　　

 

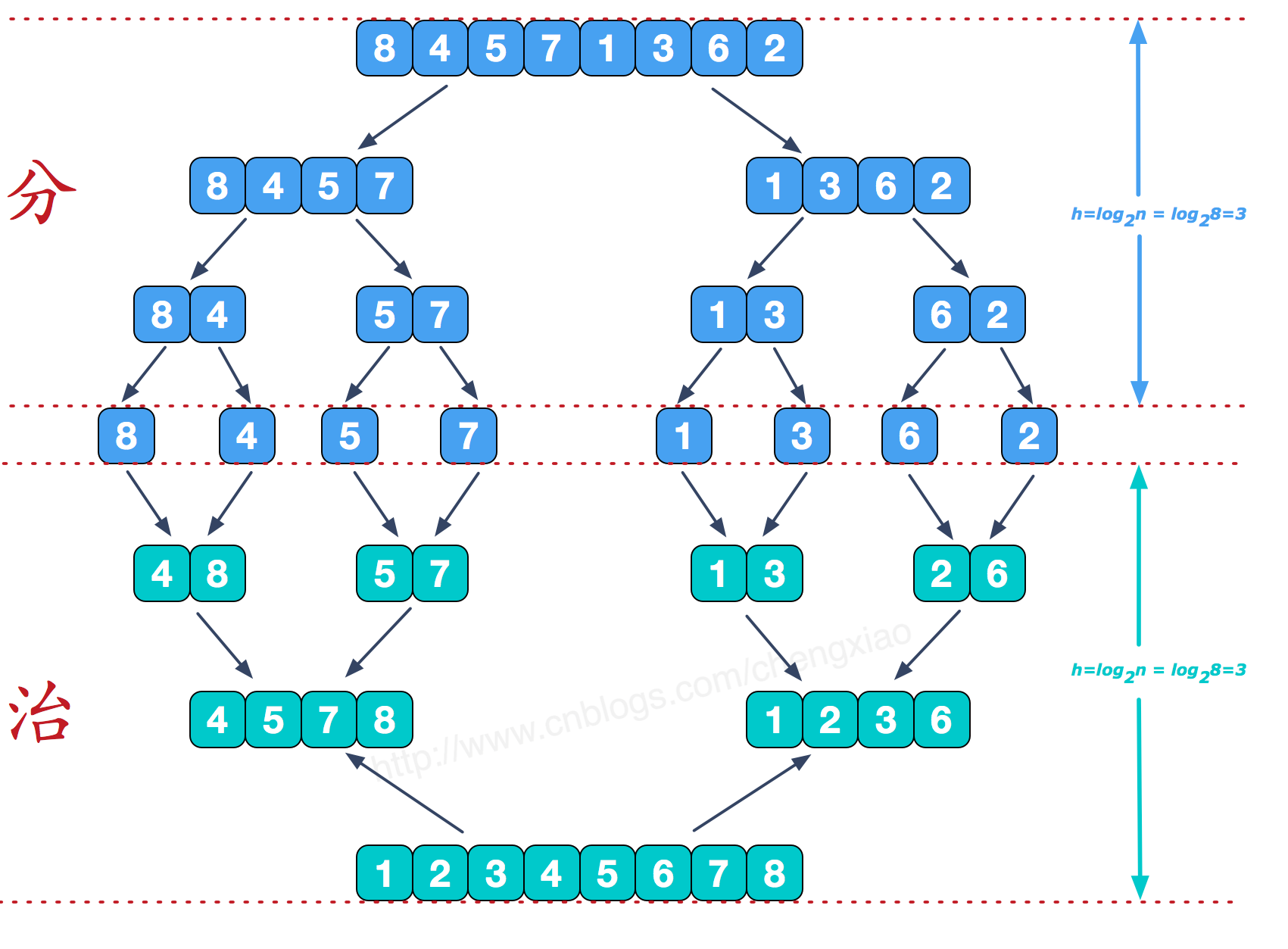
　　先拆后合，先将每个大的给拆成两个左右区间，一直拆到左右区间大小都为$1$（即只有一个元素）

　　当都拆完后，就开始合

　　合的时候就是将左右区间进行排序，可以理解为两个有序队列每次取两个队列的队头较小者

 

实现

　　代码如下：

#include<iostream>
#include<cstdio>
#define NUM 100010
using namespace std;

int n;
int a[NUM],b[NUM];

void pai( int l,int r ){
    if( l >= r ){ //叶子节点
        return;
    }
    
    int mid = (l+r) / 2;
    pai( l,mid ); //先将左右区间拆掉 
    pai( mid+1,r );
    
    
    //再回来时左右区间就都已经是各自有序的了 
    int n1 = l,n2 = mid+1; //两个"指针"记录当前两个队列中的队头位置 
    for( int i = l;i <= r;i++ ){
        
        if( n1 > mid ){ //如果左区间空了 
            b[i] = a[n2];//放右区间的队头 
            n2++;
        }else if( n2 > r ){ //如果右区间空了 
            b[i] = a[n1];
            n1++;
        }else if( a[n1] <= a[n2] ){ //如果左 <= 右 
            b[i] = a[n1];
            n1++;
        }else{ //如果右 < 左 
            b[i] = a[n2];
            n2++;
        }
    }
    
    for( int i = l;i <= r;i++ )//归纳回 a 数组 
        a[i] = b[i];
    
}
int main(){
    cin >> n;
    for( int i = 1;i <= n;i++ )
        cin >> a[i];
    pai( 1,n );  
    
    for( int i = 1;i <= n;i++ )
        cout << a[i] << " ";
    return 0;
}
归并排序

 

 典型应用：逆序对

　   例题：洛谷P1908 逆序对

 1 #include<iostream>
 2 #include<cstdio>
 3 #define NUM 500010
 4 using namespace std;
 5 
 6 int n;
 7 long long a[NUM],b[NUM];
 8 
 9 long long ans = 0;
10 void pai( int l,int r ){
11     if( l >= r ){
12         return;
13     }
14     int mid = (l+r) / 2;
15     pai( l,mid );
16     pai( mid+1,r );
17     
18     int n1 = l,n2 = mid+1;
19     for( int i = l;i <= r;i++ ){
20         if( n1 > mid ){
21             b[i] = a[n2];
22             n2++;
23         } 
24         else if( n2 > r ){
25             b[i] = a[n1];
26             n1++;
27         } 
28         else if( a[n1] <= a[n2] ){
29             b[i] = a[n1];
30             n1++;
31         }
32         else{
33             ans += mid-n1+1;//重点！！ 
34             b[i] = a[n2];
35             n2++;
36         }
37     }
38     for( int i = l;i <= r;i++ )
39         a[i] = b[i];
40 }
41 int main(){
42     scanf( "%d",&n );
43     for( int i = 1;i <= n;i++ )
44         scanf( "%d",&a[i] );
45 
46     pai( 1,n );
47     
48     printf( "%lld",ans );
49     return 0;
50 }
逆序对

 　　其中第$33$行，当右区间中有数字小于左区间，则说明有逆序对

　　 而逆序对的数量就是左区间剩余元素的个数

 

 

 

 

 





posted @ 2022-06-22 09:15  little_sheep_xiaoen  阅读(28)  评论(0)  编辑  收藏  举报