线段树
线段树的代码之前就没学明白,再复习一遍
贴一下OI Wiki给的解释
线段树的作用
众所周知线段树和树状数组都是把 普通数组 和 前缀和差分 给搞到一起,使得数组内单点修改,单点查询,区间修改,区间查询(包括求和与求最大最小值)都是$O(log N)$
线段树的结构原理
对于一个普通数组$a[6]: {X,10,11,12,13,14}$
将其转化成线段树的形态的话则为下图:
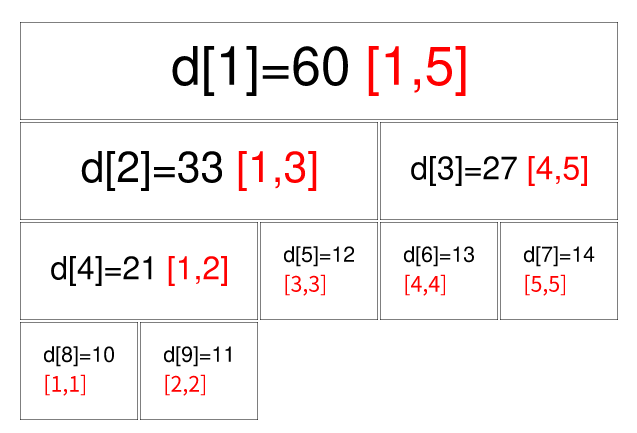
红色表示线段树中该节点$d_i$所管辖的$a$数组区间范围,如$d_1$管辖范围即$[1,5](a_1,a_2,\cdot\cdot\cdot,a_5)$
其中可以看出,$d_i$的左孩子是$d_{i\times2}$,右孩子是$d_{i\times2+1}$
而每个$d_i$存的数值就是自己所管辖的所有节点的数值和
建树
这里我们考虑递归建树,设当前节点为$p$ ,如果$p$管辖的区间长度已经是$1$(即叶子节点),则可以直接赋予其$a$数组上相应位置的值。
如果不是叶子节点,则将该区间从中点处分割为两个子区间,分别进入左右子节点递归建树,最后合并两个子节点的信息。
代码如下:

void build( int p,int l,int r ) { //该节点编号为p,管辖范围为 l-r if( l == r ){ //叶子节点 d[p] = a[l]; return; } int mid = l + ( (r-l) >> 1 ); //类似二分中的mid = l + (r-l) / 2; 防止炸int //先算加减再位运算 ,故套括号 build( p<<1,l,mid );//左孩子 build( p<<1|1,mid+1,r );//右孩子 d[p] = d[p<<1] +d[p<<1|1];//值为两个子树的值的和 }
注:线段树的数组空间要开的大一点(常为$4n$)
区间查询
原则是:能取整块就取整块
以上图为例,如要取区间$[1,5]$的和,则直接取$d_1$的值$(60)$即可
如查询区间$[3,5]$,那么就得将其拆分为两个区间$[3,3]$和$[4,5]$,通过相加取得最终的答案
代码如下:

int getsum( int l,int r,int s,int t,int p ){ // [l,r] 为查询区间, [s,t]当前节点p包含的区间 if( l <= s && t <= r ) //如询问区间包含当前区间时,直接返回当前区间的和 return d[p]; int mid = s + ( (t-s)>>1 ),sum = 0; if( l <= mid ) sum += getsum( l,r,s,mid,p*2 ); //如果左儿子代表的区间 [s,mid]与询问区间有交集, 则查询左儿子 if( r > mid ) sum += getsum( l,r,mid+1,t,p*2+1 ); //如果右儿子代表的区间 [mid+1,t]与询问区间有交集,则查询右儿子 return sum; }
区间修改
这里要用到懒惰标记了
如果整一个大块都要进行整体的增减时,直接在大块的懒惰数组中增减
懒惰标记,简单来说,就是通过延迟对节点的更改,从而减少可能不必要的操作。每次修改时,我们通过打标记的方法表明该节点对应的区间在某一次操作中被更改
如果将$[3,5]$中每个数加上$5$,那么就要在对应的$[3,3]$和$[4,5]$上打上标记
STEP 1
下图初始情况(为节省空间,不再展示节点的管辖区间)

STEP 2
对节点$[3,3]$和$[4,5]$上打上标记

这时候区间修改就结束了
如果我们这个时候查询$[4,4]$区间上的数字和的话:
STEP3
我们通过递归找到$[4,5]$ 区间,发现该区间并非我们的目标区间,且该区间上还存在标记。这时候就到标记下放的时间了。

现在$6$、$7$ 两个节点的值变成了最新的值,查询的结果也是准确的
代码如下:

ll query( int p,int l,int r,int x,int y ){ if( l >= x && r <= y ) return d[p]; int mid = (l+r) >> 1; if( tag[p] ){ d[p<<1] += tag[p] * (mid-l+1); d[p<<1|1] += tag[p] * (r-mid); tag[p<<1] += tag[p]; tag[p<<1|1] += tag[p]; tag[p] = 0; } ll sum = 0; if( mid >= x ) sum += query( p<<1,l,mid,x,y ); if( mid < y ) sum += query( p<<1|1,mid+1,r,x,y ); return sum; }

void add( int p,int l,int r,int x,int y,ll w ){ //分别为:节点编号,节点左右范围,修改范围 if( l >= x && r <= y ){ // 修改区间包含该区间时直接修改当前节点的值 tag[p] += w; d[p] += w * (r-l+1); return; } int mid = (l+r) >> 1; //如果这是叶子节点,也无需释放懒惰标记,因为上面这个if里已经改掉了其d值 if( tag[p] && l != r ){ // 如果当前节点的懒标记非空,则更新当前节点两个子节点的值和懒标记值 d[p<<1] += tag[p] * (mid-l+1); d[p<<1|1] += tag[p] * (r-mid);//更新左右孩子的数值 tag[p<<1] += tag[p]; tag[p<<1|1] += tag[p];//更新左右孩子懒数组 tag[p] = 0; } if( mid >= x ) //如果左孩子的右边界在待修范围内,即左半边有节点需要修改 add( p<<1,l,mid,x,y,w ); if( mid < y ) //如果右孩子的左边界在待修范围内,即右半边有节点需要修改 add( p<<1|1,mid+1,r,x,y,w ); d[p] = d[p<<1] +d[p<<1|1];//更新当前节点的值 }





