树链剖分
树链剖分的主要支持以下操作：
- 将树结点$x$到$y$的最短路径上所有结点加权
- 查询树结点$x$到$y$的最短路径上所有结点的权值总和
- 将以$x$为根的子树内所有结点加权
- 查询以$x$为根的子树内所有结点的权值总和
它的思想是：把一棵树拆成一条条互不相交的链，然后用数据结构去维护这些链
那么问题来了：如何把树拆成链？
首先明确一些定义
重(zhong)儿子：以该节点为根的的子树中,以该结点的孩子为根的 最多节点个数的子树(是该节点的孩子)，即为该节点的重儿子
重边：连接该节点与它的重儿子的边
重链：由重边相连得到的链
轻链：由非重边相连得到的链
这样就不难得到拆树的方法
对于每一个节点，找出它的重儿子，将重儿子连接，这棵树就自然而然的被拆成了许多重链与许多轻链
如何对这些链进行维护？
首先，要对这些链进行维护，就要确保每个链上的节点都是连续的，
因此我们需要对整棵树进行重新编号，然后利用dfs序的思想，用线段树或树状数组等进行维护
（具体用什么需要看题目要求，因为线段树比树状数组功能强大一点，这里就不提供树状数组写法了）
注意在进行重新编号的时候优先访问重链，这样可以保证重链内的节点编号连续
结合一张图来理解一下
一棵最基本的树
——————————————
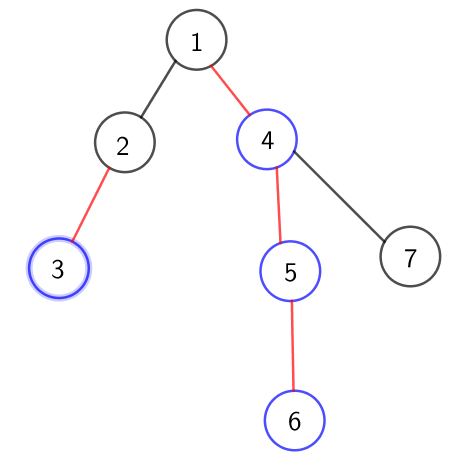蓝色为重儿子，红色为重边
———————————————
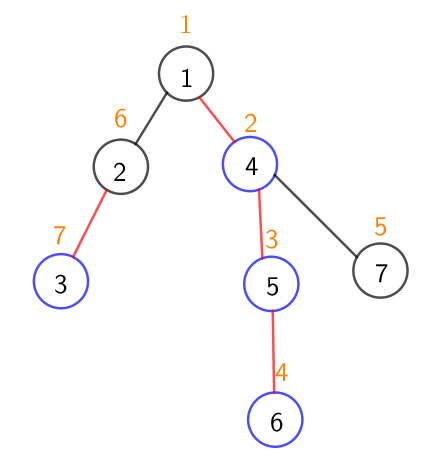对树进行重新编号
橙色表示的是按照dfs序重新编号后的序号
因为先访问重儿子，所以重链内的节点编号是连续的，于是就可以用线段树维护树上结点权值，再在线段树上搞事情啦，比如咱们要的像什么区间加区间求和什么的
而线段树中存的是每个树结点，以$i$为根的子树的树在线段树上的编号为$[i,i+$子树节点数$-1]$（子树结点包含自己）
接下来结合一道例题，加深一下对于代码的理解
代码
首先来一坨定义
int deep[MAXN];//节点的深度 int fa[MAXN];//节点的父亲 int son[MAXN];//节点的重儿子 int tot[MAXN];//节点子树的大小
第一步
按照我们上面说的，我们首先要对整棵树跑一遍dfs，找出每个节点的重儿子
顺便处理出每个节点的深度，以及他们的父节点
int dfs1( int now,int f,int dep ){ deep[now]=dep; fa[now]=f; tot[now] = 1;//子树里有自己 int maxson = -1;//初始化没有重孩子 for( int i=head[now];i != -1;i = edge[i].next ){ if( edge[i].to == f ) continue; tot[now] += dfs1( edge[i].v,now,dep+1 );//加上每个孩子的子树大小 if( tot[edge[i].v] > maxson ) maxson = tot[edge[i].v],son[now]=edge[i].v; } return tot[now];//返回以他为根的子树大小 }
第二步
然后我们需要对整棵树进行重新编号
我把一开始的每个节点的权值存在了$b$数组内
void dfs2(int now,int topf){ idx[now] = ++cnt; //dfs序 a[cnt] = b[now]; //b[i]为原序列中每个结点的权值 top[now] = topf; //top[i]存下过该点的重链起点 if( !son[now] ) return ; dfs2( son[now],topf ); for( int i = head[now];i != -1;i = edge[i].nxt ) if( !idx[edge[i].v] ) //如果这个孩子之前没有被访问过 dfs2( edge[i].v,edge[i].v ); }
$idx$表示重新编号后该节点的编号是多少 另外，这里引入了一个$top$数组，
$top[i]$表示$i$号节点所在重链的头节点(最顶上的节点)
这个数组在后面的区间修改查询有用
第三步
我们需要根据重新编完号的树，把这棵树的上每个点映射到线段树上，
struct tree{ int l,r,siz;//siz是该结点范围大小 int w,f;//该结点的权值以及他的父节点 }; tree t[MAXN]; void build( int now,int ll,int rr ){ t[now].l=ll;t[now].r=rr; t[now].siz=rr-ll+1; if(ll==rr){ t[now].w=a[ll]; //将树上的结点以dfs序为线段树叶子编号存在线段树中 return; } int mid = ( ll+rr ) >> 1; build( now<<1,ll,mid ); build( now<<1|1,mid+1,rr); update(now); }
另外的线段树基本操作， 这里就不详细解释了，直接放代码
//线段树常用操作 void update(int now){ //更新 t[now].w = ( t[now<<1].w + t[now<<1|1].w + MOD ) % MOD; } void add( int now,int ll,int rr,int val ){ //区间加 if( ll <= t[now].l && t[now].r <= rr ){ t[now].w += t[now].siz*val; t[now].f += val; return; } pushdown(now); int mid=( t[now].l+t[now].r )>>1; if( ll <= mid ) add( now<<1,ll,rr,val ); if( rr > mid ) add( now<<1|1,ll,rr,val ); update(now); } int query( int now,int ll,int rr ){ //区间求和 int ans = 0; if( ll <= t[now].l && t[now].r <= rr ) return t[now].w; pushdown(now); int mid = ( t[now].l + t[now].r ) >> 1; if( ll <= mid ) ans = ( ans + query(now<<1,ll,rr) ) % MOD; if( rr > mid ) ans = ( ans + query(now<<1|1,ll,rr) ) % MOD; return ans; } void pushdown( int now ){//下传标记 if( !t[now].f ) return ; t[now<<1].w = ( t[now<<1].w + t[now<<1].siz*t[now].f ) % MOD; t[now<<1|1].w = ( t[now<<1|1].w + t[now<<1|1].siz*t[now].f ) % MOD; t[now<<1].f = ( t[now<<1].f + t[now].f) % MOD; t[now<<1|1].f = ( t[now<<1|1].f + t[now].f) % MOD; t[now].f = 0; }
第四步
我们考虑如何实现对于树上的操作
树链剖分的思想是:对于两个不在同一重链内的节点,让他们不断地跳,使得他们处于同一重链上
那么如何"跳”呢？
还记得我们在第二次$dfs$中记录的$top$数组么？
有一个显然的结论：$x$到$top[x]$中的节点在线段树上是连续的，
结合$deep$数组
假设两个节点为$x,y$
我们每次让$deep[top[x]]$与$deep[top[y]]$中大的(在下面的)往上跳(有点类似于树上倍增)
让x节点直接跳到$top[x]$,然后在线段树上更新
最后两个节点一定是处于同一条重链的，前面我们提到过重链上的节点都是连续的，直接在线段树上进行一次查询就好
void query( int x,int y ){ //x与y路径上的和 int ans=0; while(top[x]!=top[y]) { if(deep[top[x]]<deep[top[y]]) swap(x,y); ans=(ans+query(1,idx[ top[x] ],idx[x]))%MOD; x=fa[ top[x] ]; } if(deep[x]>deep[y]) swap(x,y); ans=(ans+query(1,idx[x],idx[y]))%MOD; printf("%d\n",ans); } void add_shu(int x,int y,int val ){ //对于x,y路径上的点加val的权值 while( top[x] != top[y] ){ if( deep[top[x]] < deep[top[y]] ) swap(x,y); add( 1,idx[top[x]],idx[x],val ); x = fa[top[x]]; } if( deep[x] > deep[y] ) swap(x,y); add(1,idx[x],idx[y],val); }
在树上查询的这一步可能有些抽象，我们结合一个例子来理解一下
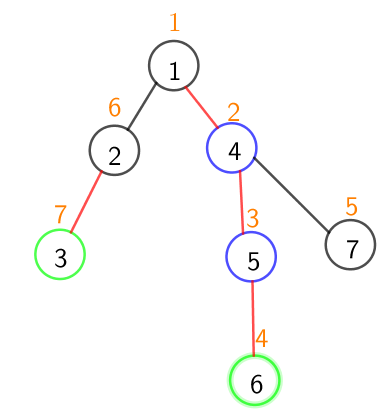
还是上面那张图，假设我们要查询$3.6$这两个节点的之间的点权合，为了方便理解我们假设每个点的点权都是$1$
刚开始时
$top[3]=2,top[6]=1$
$deep[top[3]]=2,deep[top[6]]=1$
我们会让$3$向上跳,跳到$top[3]$爸爸,也就是$1$号节点
这时$1$号节点和$6$号节点已经在同一条重链内,所以直接对线段树进行一次查询即可
对于子树的操作
这个就更简单了
因为一棵树的子树在线段树上是连续的
所以修改的时候直接这样
$IntervalAdd(1,idx[x],idx[x]+tot[x]-1,z%MOD);$
时间复杂度
性质1
如果边$\left( u,v\right)(u,v)$为轻边,那么$Size\left( v\right) \leq Size\left( u\right) /2Size(v)≤Size(u)/2$。
证明：显然，否则该边会成为重边
性质2
树中任意两个节点之间的路径中轻边的条数不会超过$\log _{2}nlog2n$,重路径的数目不会超过$\log _{2}nlog2n$
证明：不会
有了上面两条性质，我们就可以来分析时间复杂度了
由于重路径的数量的上界为$\log _{2}nlog2n$，
线段树中查询/修改的复杂度为$\log _{2}nlog2n$
那么总的复杂度就是$\left( \log _{2}n\right) ^{2}(log2n)2$
#include<iostream> #include<cstdio> #include<cstring> using namespace std; const int mAXn=2*1e6+10; #define ls k<<1 #define rs k<<1|1 struct node { int u,v,nxt; }edge[mAXn]; int head[mAXn]; int num=1; struct tree { int l,r,w,siz,f; }t[mAXn]; int n,m,root,mOD,cnt=0,a[mAXn],b[mAXn]; inline void AddEdge(int x,int y) { edge[num].u=x; edge[num].v=y; edge[num].nxt=head[x]; head[x]=num++; } int deep[mAXn],fa[mAXn],son[mAXn],tot[mAXn],top[mAXn],idx[mAXn]; int dfs1(int now,int f,int dep) { deep[now]=dep; fa[now]=f; tot[now]=1; int maxson=-1; for(int i=head[now];i!=-1;i=edge[i].nxt) { if(edge[i].v==f) continue; tot[now]+=dfs1(edge[i].v,now,dep+1); if(tot[edge[i].v]>maxson) maxson=tot[edge[i].v],son[now]=edge[i].v; } return tot[now]; } void update(int k){ t[k].w=(t[ls].w+t[rs].w+mOD)%mOD; } void Build(int k,int ll,int rr){ t[k].l=ll;t[k].r=rr;t[k].siz=rr-ll+1; if(ll==rr){ t[k].w=a[ll]; return ; } int mid=(ll+rr)>>1; Build(ls,ll,mid); Build(rs,mid+1,rr); update(k); } void dfs2(int now,int topf){ idx[now]=++cnt; a[cnt]=b[now]; top[now]=topf; if(!son[now]) return ; dfs2(son[now],topf); for(int i=head[now];i!=-1;i=edge[i].nxt) if(!idx[edge[i].v]) dfs2(edge[i].v,edge[i].v); } void pushdown(int k){ if(!t[k].f) return ; t[ls].w=(t[ls].w+t[ls].siz*t[k].f)%mOD; t[rs].w=(t[rs].w+t[rs].siz*t[k].f)%mOD; t[ls].f=(t[ls].f+t[k].f)%mOD; t[rs].f=(t[rs].f+t[k].f)%mOD; t[k].f=0; } void add(int k,int ll,int rr,int val){ if(ll<=t[k].l&&t[k].r<=rr){ t[k].w+=t[k].siz*val; t[k].f+=val; return ; } pushdown(k); int mid=(t[k].l+t[k].r)>>1; if( ll <= mid ) add(ls,ll,rr,val); if( rr > mid ) add(rs,ll,rr,val); update(k); } void add_shu(int x,int y,int val){ while(top[x]!=top[y]){ if(deep[top[x]]<deep[top[y]]) swap(x,y); add(1,idx[ top[x] ],idx[x],val); x=fa[ top[x] ]; } if(deep[x]>deep[y]) swap(x,y); add(1,idx[x],idx[y],val); } int query(int k,int ll,int rr){ int ans=0; if(ll<=t[k].l&&t[k].r<=rr) return t[k].w; pushdown(k); int mid=(t[k].l+t[k].r)>>1; if(ll<=mid) ans=(ans+query(ls,ll,rr))%mOD; if(rr>mid) ans=(ans+query(rs,ll,rr))%mOD; return ans; } void treeSum(int x,int y){ int ans=0; while(top[x]!=top[y]){ if(deep[top[x]]<deep[top[y]]) swap(x,y); ans=(ans+query(1,idx[ top[x] ],idx[x]))%mOD; x=fa[ top[x] ]; } if(deep[x]>deep[y]) swap(x,y); ans=(ans+query(1,idx[x],idx[y]))%mOD; printf("%d\n",ans); } int main(){ memset(head,-1,sizeof(head)); cin >> n >> m >> root >> mOD; for(int i=1;i<=n;i++) cin >> b[i]; for(int i=1;i<=n-1;i++){ int x,y; cin >> x >> y; AddEdge(x,y);AddEdge(y,x); } dfs1(root,0,1); dfs2(root,root); Build(1,1,n); while(m--){ int opt,x,y,z; cin >> opt; if(opt==1){ cin >> x >> y >> z; z=z%mOD; add_shu(x,y,z); } else if(opt==2){ cin >> x >> y; treeSum(x,y); } else if(opt==3){ cin >> x >> z; add(1,idx[x],idx[x]+tot[x]-1,z%mOD); } else if(opt==4){ cin >> x; printf("%d\n",query(1,idx[x],idx[x]+tot[x]-1)); } } return 0; }
