扫描线

扫描线就是一条直线在坐标系中平移，一点一点扫其有用的平行线

普通扫描线最基本的应用就是对坐标系上多个矩形进行切割来求他们的总覆盖面积

比如

那具体怎么操作呢？

看到最后一步图片的虚线了吗？

所以我们来模拟一波

其中这条移动的线就是扫描线

那做法就很明显了：

我们记录每一条竖直方向上的线段（一个含$x$坐标，上端y坐标$yh$，下端y坐标$yl$，加减的标记$flag$的四元组$(x,yh,yl,k)$）

将所有竖边的端点高度排序得到序列$rt[i]$，再将每个边所在的x坐标排序得到序列$val[i]$

变成这样↓

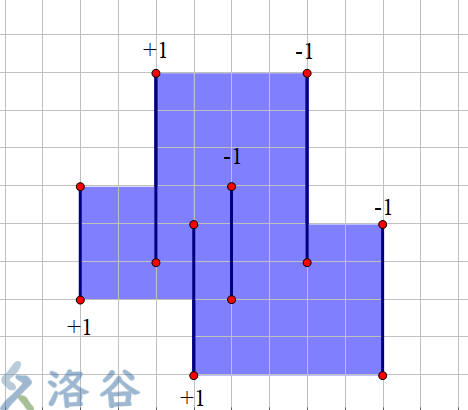
然后维护扫描线上被覆盖的长度就好了！！！

最后如何维护这条扫描线呢？

线段树闪亮登场

每次修改之后，更新线段树中节点的$len$(被覆盖的长度)

至此，本题已经基本解决了！

为什么说是基本呢？当然是还有优化啦

学过线段树的都知道懒惰标记，不过这题还有不用懒惰标记的优化！

话说懒惰标记.....

可以使区间修改不用全部下传至叶子节点，在查询子节点的值时才下传，

从而保证完成操作的时间在 $O$ $(\log n) $ 内的方法

查询子节点的值？？

我们不是只查询全图最低点到最高点的值，也就是，根节点的值吗？

于是，我们想到，除左右端点$l,r$之外，在线段树的每个节点上维护两个值：

　　该节点代表的区间被矩形覆盖的长度$len$，该节点自身被覆盖的次数$cnt$。最初，二者均为0.

对于每一个$(x,yh,yl,flag)$，我们再$[val[yh],val[yl]-1]$上执行区间修改。该区间被线段树划分成 $\log$ $n$ 个节点，我们把这些节点的$cnt$都加$k$。

对于线段树中任意一个节点 $[l,r]$，若$cnt > 0$，即该点被覆盖，则$len$等于$val(r+1)-val(l)$


否则，该点$len$等于两个子节点的$len$之和

在一个节点的$cnt$被修改，以及线段树从下往上传递信息时，我们都按照该方法更新$len$值。根节点的$len$值就是整个扫描线上被覆盖的长度

刷一道板子：  洛谷P5490 扫描线【模板】

#include<iostream>
#include<cstdio>
#include<algorithm>
#define ls (rt << 1)//左儿子
#define rs (rt << 1 | 1)//右儿子
#define NUM 4000010
#define ll long long
using namespace std;
int n,cnt;
ll x1,x2,y1,y2,x,y;
ll maxn = 1 << 31;//maxn防止超边界 
ll rk[NUM],val[NUM];//val是竖线离散化后的排序 

struct tree{
    int l,r;//区间左右端点
    ll cnt,len;//如上所述，len是覆盖长度，cnt是覆盖次数 
};
tree t[NUM];

struct xian{
    ll x,yh,yl;//yh是竖线最高高度，yl是竖线最低高度 
    int flag;
};
xian e[NUM]; //记录每一条竖线

void pushup(ll rt) {
    if( (t[rt].l == maxn && t[rt].r == maxn) ) return;//如果超出范围，直接退出  
    if( t[rt].cnt ) t[rt].len = val[t[rt].r+1] - val[t[rt].l];//如果结点被覆盖 
    //该结点的长度就是横坐标中右减左 
    else t[rt].len = t[ls].len + t[rs].len;//没被覆盖，长度就是两孩子的长度和 
}//向上更新节点

void build( ll rt,ll l,ll r) { //建树基本操作 
    t[rt].l = l, t[rt].r = r;
    if ( l == r ) return;
    ll mid = ( t[rt].l + t[rt].r ) >> 1;
    build( ls,l,mid );
    build( rs,mid+1,r);
}

void add( ll rt,ll l,ll r,ll v) { //将范围中每个点都更改其值 
    if(l <= t[rt].l && t[rt].r <= r){ //区间完全覆盖该点 
        t[rt].cnt += v;
        pushup(rt);
        return;
    }
    ll mid = ( t[rt].l + t[rt].r ) >> 1;
    if ( l <= mid) add( ls,l,r,v );
    if (mid < r) add( rs,l,r,v );
    pushup(rt);
}//基本操作，不再赘述

bool cmp( xian a,xian b ){
    if( a.x != b.x ) return a.x < b.x;
    return a.flag > b.flag;
}

int main(){
    cin >> n;
    ll ans = 0;
    for( int i = 1;i <= n;i++){
        cin >> x1 >> y1 >> x2 >> y2;
        e[i*2-1].x = x1;
        e[i*2].x = x2;
        e[i*2-1].yh = y2;
        e[i*2].yh = y2;
        e[i*2-1].yl = y1;
        e[i*2].yl = y1;
        e[i*2-1].flag = 1;
        e[i*2].flag = -1;//flag表示该边是矩形的左边界或右边界
        rk[++cnt] = y1;
        rk[++cnt] = y2;//每个矩形横线的纵坐标，也就是每条纵线的端点纵坐标 
    }
    sort( rk+1,rk+n*2+1 );//排序
    cnt = unique( rk+1,rk+n*2+1 )-rk-1;//去重
    for( int i = 1;i <= 2*n;i++ ){
        ll pos1 = lower_bound( rk+1,rk+cnt+1,e[i].yh ) - rk;
        ll pos2 = lower_bound( rk+1,rk+cnt+1,e[i].yl ) - rk;//在数组中二分查找当前边两端点的位置
        val[pos1] = e[i].yh;
        val[pos2] = e[i].yl;//val[i]就是第i个端点的x坐标 
        e[i].yh = pos1;
        e[i].yl = pos2;//这里才是离散化！ 
        maxn = max( maxn, pos1 );//设定边界 
    }
    sort( e+1,e+2*n+1,cmp );//按照x坐标将竖线排序 
    build( 1,1,n<<1 );//一共点的数量为n*2 
    for( int i = 1;i < 2*n;i++){
        add( 1,e[i].yl,e[i].yh-1,e[i].flag );//区间加flag
        ans += t[1].len * ( e[i+1].x-e[i].x );//根节点的len值*与下一条线段的距离=这一块内的矩形面积
    }
    cout << ans << endl;
    return 0;
}

 

 

详解