容斥原理
容斥原理：
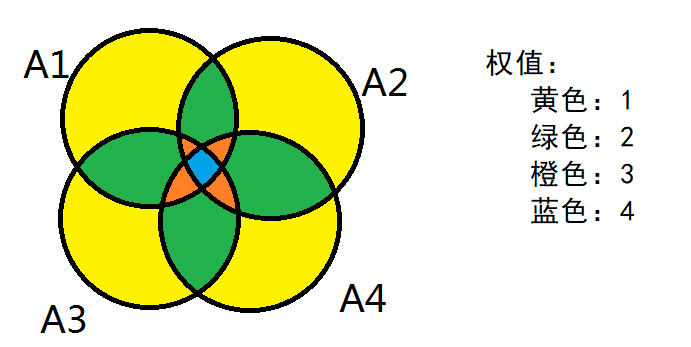
经常题目要求算整个的总面积，也就是所有的 “黄+绿+橙+蓝”，即四个圆的并集
但我们大多数时候不仅仅是四个圆的总面积，一般是多个圆，这里以四个圆来举例说明
先上公式：
$\left\vert \bigcup_1^3 A_i \right\vert = \sum_{i=1}^{n}\left\vert A_i \right\vert - \sum_{i,j:i \ne j } \left\vert A_i \bigcap A_j \right\vert + \sum_{i,j,k:i \ne j \ne k} \left\vert A_i \bigcap A_j \bigcap A_k \right\vert - \cdot\cdot\cdot + \left\vert A_i \bigcap \cdot\cdot\cdot \bigcap A_n \right\vert $
（对的式子很长，打了好久）
通过公式的分析可以看出，就是加奇数个，减偶数个
为什么？将公式分成部分来分析也不是很难理解：
第一部分：\sum_{i=1}^{n}\left\vert A_i \right\vert
这部分最后算出来应该是 ：黄$\times 1 + $ 绿$\times 2 + $ 橙$\times 3 + $ 蓝$\times 4$
显然，绿色多加了一遍，橙色多加了两遍，蓝色多加了三遍
所以要减掉他们
第二部分：\sum_{i,j:i \ne j } \left\vert A_i \bigcap A_j \right\vert
这部分是要减去的，算出来就是：绿$\times 1 + $橙 $\times 2 + $ 蓝$\times 3$（错误）
让我们来看一下为啥这玩意错了：
注意公式中，$\sum_{i,j:i \ne j} \left\vert A_i \bigcap A_j \right\vert$说的是任意两个A_i，A_j之间的交集
但绿$\times 1 +$ 橙$\times 2 +$ 蓝$\times 3$ 是只有 $A_1 \bigcap A_2 $、$A_1 \bigcap A_3 $、$A_2 \bigcap A_3 $、$A_3 \bigcap A_4 $
发现了吗？少了$A_1 \bigcap A_4 $ 和 $A_2 \bigcap A_3 $，也就是对角线之间的交集。
这块之前漏加的里面包含了 橙 $\times 1 +$ 蓝 $\times 2$
所以总的第二部分减去了 绿$\times 1 +$ 橙$\times 3 +$ 蓝$\times 5$
不论如何，用这部分减掉第一部分，就剩下了：
黄$\times 1 + $ 绿$\times 1 +$ 橙$\times 0 +$ 蓝$\times-2$
我们这时会发现，橙色没有了，橙色反而还少了！
那就再加回来吧
第三部分：$\sum_{i,j,k:i \ne j \ne k} \left\vert A_i \bigcap A_j \bigcap A_k \right\vert$
这部分是要加上的，算出来就是：橙$\times 1 +$ 蓝$\times 4$
这时候我们手里就有了 黄$\times 1 + $ 绿$\times 1 +$ 橙$\times 1 +$ 蓝$\times 2$
第四部分是 $\sum_{i,j,k,t:i \ne j \ne k \ne t} \left\vert A_i \bigcap A_j \bigcap A_k \bigcap A_t \right\vert$
这就是只是单纯减去中间的蓝色了，即 蓝 $\times 1$
所以我们这时候手里的就是 黄$\times 1 + $ 绿$\times 1 +$ 橙$\times 1 +$ 蓝$\times 1$ 了！
整个过程其实就很像转魔方，一步配好一层，配好了就不再动他了
通过模拟了一下四个圆的容斥，可以证明出这个公式是正确的，
需要注意的是以下几个方面：
1. 求单独一步的时候要将所有集合的交集算进去，避免出现第二步开始的错误
2. 整个公式是加奇减偶，万万不可忘记变号
3. 公式中的这些交集是包含了所有这几个圆相交的所有部分
如 $ A_1 \bigcap a_2$ 其实是包括了对应的绿+橙+蓝
做个题练练手：
| |
| |
| |
| |
\ | | /
\ | | /
\ /
\ /
答案为 A ，一共是有 120 个学生
根据题意可知：$\sum_{i=1}^{n}\left\vert A_i \right\vert$ 就是 $63 + 89 + 47 = 199$
$\sum_{i,j,k:i \ne j \ne k} \left\vert A_i \bigcap A_j \bigcap A_k \right\vert$ 就是最中间的 $24$
这时候问题来了，\sum_{i,j:i \ne j } \left\vert A_i \bigcap A_j \right\vert 怎么求
刚才提醒过了，这个\sum_{i,j:i \ne j } \left\vert A_i \bigcap A_j \right\vert是两圆相交的所有部分，
设这三个数分别是 $x、y、z$，由题意得 $ x + y + z = 46 $，
则第二部分就应该是 $ ( x + 24 ) + ( y + 24 ) + ( z + 24 ) = ( x + y + z ) + 24 \times 3 = 118 $
用公式求一求，总和就是 $199 - 118 + 24 = 105$
就算有 105 这个选项也不能选，因为这里面还不包括“啥也不选”的 15 个人呢！
所以答案就是 120 个人
That's all，thanks for your reading！
