迪杰斯特拉
今天的主题:
迪杰斯特拉(单源最短路)
先说说迪杰的思路:
1. 从所有没有被当过转折点的点中,找出当前距离起点最近的那个点 ——> $\color{green}{O(n)}$ 复杂度}
2. 用当前的点更新所有剩余点的距离
3. 共$n$个点,故运行$n$次 ——> $\color{green}{O(n)}$ 复杂度}
这3步对于朴素算法就都是for循环,其中,3套着1和2,即$O(n^2)$复杂度
然后堆优化的话可以降到$O(n log_2 n)$
是这个样子,无向图可以用邻接矩阵 $O( n^2 )$ 或 邻接表 $O( nm )$ 存;
有向图可以用前向星 $O( n+m )$ 存;
无向图
下面这个是用邻接矩阵打的无向图:

#include<iostream> #include<cstdio> using namespace std; int n,m,start,q; const int inf = 100001; int a[10010][10010];//邻接表 int d[10010],f[10010]; void zuiduan() { //算法核心 for (int i = 1;i <= n;i++){ d[i] = inf; f[i] = false; } d[start] = 0; for( int i = 1;i <= n;i++ ){ int mind = inf;//最短的距离 int k; for( int j = 1;j <= n;j++ ) if( !f[j] && d[j] < mind ){ mind = d[j];//这就是最短的距离 k = j;//找到最近的点 } if( mind == inf ) break;//没有最近的点 f[k] = 1;//该结点已经访问过 for( int j = 1; j <= n; j++ ) if( (!f[j]) && (d[k] + a[k][j] < d[j]) ){ d[j] = d[k] + a[k][j];//用转折点更新该节点 } } } int main() { cin >> n >> m >> start;//结点个数、边的数量、起点 int x,y,w; for( int i = 1;i <= n;i++ ) for( int j = 1;j <= n;j++ ){ if(j == i) a[i][j] = 0; else a[i][j] = inf;//初始化 } for( int i = 1;i <= m;i++ ){ cin >> x >> y >> w; a[x][y] = w; a[y][x] = w;//无向图存两遍 } zuiduan();//迪杰 for( int i = 1;i <= n;i++ ) if( i != start ){ printf( "点%d的距离为%d\n",i,d[i] ); } return 0; } /*一组样例 7 6 1 1 3 1 1 6 17 7 6 9 6 4 25 2 3 10 3 5 13 */
这个被我涂黄的地方是我前一段时间一直不太理解的一个点,不过还好,现在能给出一个像样子的解释:
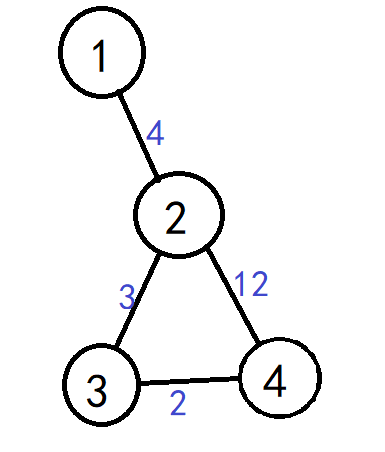
对,就是这样的当时有点迷糊:
原本的想法:1->2->3->4 的顺序没问题,但是从 点2 更新 点4 的时候,这个 $a[2][4]$ 不是最短啊,为啥还能对啊?
解释:用 点2 去更新 点4 的时候,确实不是最值,但用 点3 去更新它的时候就没问题了,
即对于点A,在所有 $d[x] < d[A]$ 的点中,距离 点A 最近的 点B,必然比 点A 先更新,则此时的 $d[B] + a[B][A]$ 必然是最小的 $d[A]$,
因为最短路不可能来自一个比 点A 距离起点更远的 点C,使得 $d[C] > d[A]$ 且 $d[C] + a[C][A] < d[A]$,因为这玩意都不满足数学公式。。。
你这家伙也太费了吧。。。这点简单的东西都想这么久。。。
为什么dij不能处理负边权
再一次遇到这个问题,正好看到了原因,备注一下

第一轮将B设为最近点,去更新C然而更新不到,故最终d[B] = -1
如果图中都是正数,在第一轮将B设为最近点时,就保证了$AC > AB$,也就是$AC+BC > AB$
所以dij不能解决负边权
有向图
然后就是有向图。
有向图的最好方式就是前向星,主要是占空间小
见代码:

#include<iostream> #include<cstdio> #define NUM 10010 #define INF 0x7f7f7f using namespace std; struct bian{ int next,to,zhi; }; bian e[NUM]; int n,m,start,cnt,k; int head[NUM],d[NUM]; bool v[NUM]; void cun( int x,int y,int w ){ e[++cnt].next = head[x]; e[cnt].to = y; e[cnt].zhi = w; head[x] = cnt; } void dijkstra(){ for( int i = 1;i <= n;i++ ){ v[i] = 0; d[i] = INF; } d[start] = 0; for( int fi = 1;fi <= n;fi++ ){ int lin = INF; for( int i = 1;i <= n;i++ ) if( !v[i] && d[i] < lin ){ k = i; lin = d[i]; } if( lin == INF ) break; v[k] = 1; for( int i = head[k];i;i = e[i].next ){ int p = e[i].to; if( !v[p] && d[p] > d[k] + e[i].zhi ) d[p] = d[k] + e[i].zhi; } } } int main() { cin >> n >> m >> start; for( int i = 1;i <= m;i++ ){ int x,y,w; cin >> x >> y >> w; cun( x,y,w ); } dijkstra(); for( int i = 1;i <= n;i++ ) if( i != start ) printf( "点%d到起点的距离为%d\n",i,d[i] ); return 0; } /*一组样例 7 6 1 1 3 1 1 6 17 6 7 9 6 4 25 3 2 10 3 5 13 输出: 11 1 42 14 17 26 */
好的,以上就是朴素的迪杰斯特拉,等我学完堆优化再来补充
堆优化
咕了好久的博客终于更了(捂脸)
堆优化了一步,就是让取最短的距离那一步快了,原本的做法是遍历一遍找最短,其中优化后可以将这一步的复杂度降到堆的$log_2 n$
不过每个节点都更新的那个$O(n)$是消不掉了
代码如下

#include<iostream> #include<cstdio> #include<queue> #define NUM 100010 #define INF 0x7f7f #define int long long using namespace std; int n,m,s; struct bian{ int to,next; long long zhi; }; bian e[NUM*5]; struct dian{ int id; long long dis; bool operator < ( const dian &x ) const{ return x.dis < dis; } }; int head[NUM]; int cnt; long long d[NUM]; int vis[NUM]; void add( int x,int y,long long w ){ e[++cnt].next = head[x]; e[cnt].to = y; e[cnt].zhi = w; head[x] = cnt; } priority_queue <dian> q; void dij(){ for( int i = 1;i <= n;i++ ) d[i] = 1e10; d[s] = 0; dian lin; lin.dis = 0;lin.id = s; q.push(lin); dian ff; int to,id,dis; while( !q.empty() ){ ff = q.top(); q.pop(); dis = ff.dis;id = ff.id; if( vis[id] ) continue; vis[id] = 1; for( int i = head[id];i;i = e[i].next ){ to = e[i].to; // if( vis[to] ) continue; if( d[to] > d[id] + e[i].zhi ){ d[to] = d[id] + e[i].zhi; lin.dis = d[to]; lin.id = to; if( !vis[to] ) q.push(lin); } } } } signed main(){ cin >> n >> m >> s; int x,y; long long w; for( int i = 1;i <= m;i++ ){ cin >> x >> y >> w; // if( x == y ) continue; add( x,y,w ); } dij(); for( int i = 1;i <= n;i++ ) cout << d[i] << " "; return 0; }





