快速排序算法详解
快速排序算法详解
快速排序是对冒泡排序的一种改进，由 C.A.R.Hoare（Charles Antony Richard Hoare，东尼·霍尔）在 1962 年提出。
快速排序的基本思想是：
通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据比另一部分的所有数据要小，再按这种方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，使整个数据变成有序序列。
快速排序的原理
排序算法的思想非常简单，在待排序的数列中，我们首先要找一个数字作为基准数（这只是个专用名词）。为了方便，我们一般选择第 1 个数字作为基准数（其实选择第几个并没有关系）。接下来我们需要把这个待排序的数列中小于基准数的元素移动到待排序的数列的左边，把大于基准数的元素移动到待排序的数列的右边。这时，左右两个分区的元素就相对有序了；接着把两个分区的元素分别按照上面两种方法继续对每个分区找出基准数，然后移动，直到各个分区只有一个数时为止。
这是典型的分治思想，即分治法。下面我们对一个实际例子进行算法描述，讲解快速排序的排序步骤。
以 47、29、71、99、78、19、24、47 的待排序的数列为例进行排序，为了方便区分两个 47，我们对后面的 47 增加一个下画线，即待排序的数列为 47、29、71、99、78、19、24、47。
首先我们需要在数列中选择一个基准数，我们一般会选择中间的一个数或者头尾的数，这里直接选择第 1 个数 47 作为基准数，接着把比 47 小的数字移动到左边，把比 47 大的数字移动到右边，对于相等的数字不做移动。所以实际上我们需要找到中间的某个位置 k，这样 k 左边的值全部比 k 上的值小，k 右边的值全部比 k 上的值大。
接下来开始移动元素。怎么移动呢？其实冒泡排序也涉及对元素的移动，但是那样移动起来很累，比如把最后一个元素移动到第 1 个，就需要比较 n-1 次，同时交换 n-1 次，效率很低。其实，只需把第 1 个元素和最后一个元素交换就好了，这种思想是不是在排序时可以借鉴呢？之前说快速排序就是对冒泡排序的一个改进，就是这个原因。
快速排序的操作是这样的：首先从数列的右边开始往左边找，我们设这个下标为 i，也就是进行减减操作（i--），找到第 1 个比基准数小的值，让它与基准值交换；接着从左边开始往右边找，设这个下标为 j，然后执行加加操作（j++），找到第 1 个比基准数大的值，让它与基准值交换；然后继续寻找，直到 i 与 j 相遇时结束，最后基准值所在的位置即 k 的位置，也就是说 k 左边的值均比 k 上的值小，而 k 右边的值都比 k 上的值大。
所以对于上面的数列 47、29、71、99、78、19、24、47，进行第 1 趟第 1 个交换的排序情况如下，第 1 次的操作情况如图 1 所示。
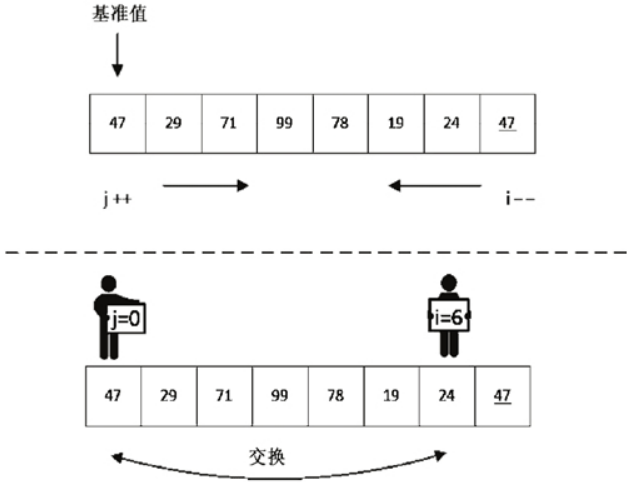
图 1 第 1 次发现可以交换的数
交换之后，j 移动到了下标为 6 的位置，对 i 继续扫描，如图 2 所示。
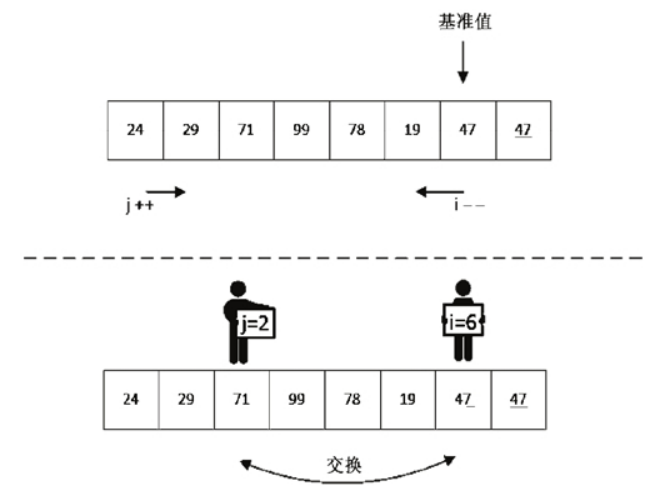
图 2 第 2 次发现可交换的值
此时交换后的数列变为 24、29、47、99、78、19、71、47。接下来我们继续对 i、j 进行操作，如图 3 所示，继续进行 i-- 及 j++ 的比较操作。
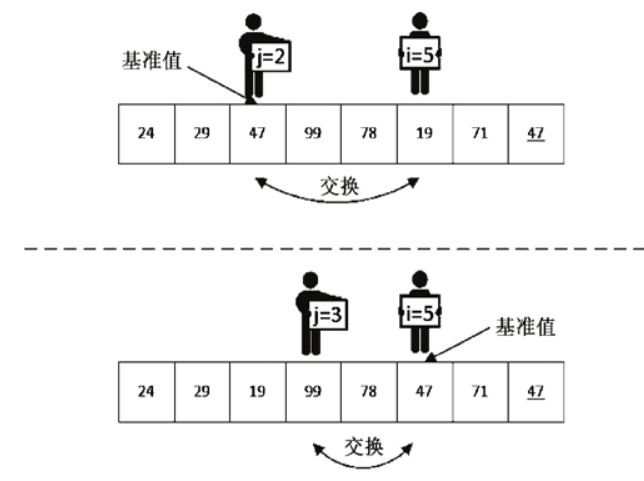
图 3 继续进行 i 与 j 的移动
进行了这两次 i、j 的移动、比较、交换之后，我们最终得到的数列是 24、29、19、47、78、99、71、47。接下来我们继续进行 i-- 的操作，发现在 i 为 4 时比 47 大不用交换，在 i 为 3 时与 j 相遇，这时就不需要继续移动、比较了，已经找到 k 了，并且 k 的值为 3。我们可以确认一下当前的数列是不是 k 左边的值都比 47 小，而 k 右边的值都比 47 大（由于要保持相对位置不变，所以 47 同样在基准值 47 的右边）。
47 这个值已经落到了它该在的位置，第 1 趟排序完成了。接下来就是以 k 为基准，分为两部分，然后在左右两部分分别执行上述排序操作，最后数据会分为 4 部分；接着对每部分进行操作，直到每部分都只有一个值为止。
接下来进行第 2 趟排序，现在左边部分为 24、29、19，我们选择第 1 个数 24 作为基准数，接着进行 i--、j++ 的操作，我们发现 i 最初的值为 19，比 24 这个基准值小，所以与基准值进行交换，得到的数列为 19、29、24；当 j 为 1 时，我们发现 29 比 24 大，所以与基准值进行交换，得到的数列 19、24、29，此时 i 为 2，j 为 1；继续 i-- 时发现 i 为 1，与 j 相遇，左边部分的数列的 k 为 1，并且左右两部分分别只有一个元素，此时第 2 轮排序的左边部分的排序结束，同时左边部分的所有数据都排序完成。
我们接着看右边部分的排序，待排序的数列为 78、99、71、47，我们同样选择第 1 个值 78 为基准值，接下来进行 i 与 j 的移动与比较，发现 47 比 78 小，进行交换，得到的数列 47、99、71、78；从左往右发现 99 比基准值 78 大，进行交换，得到的数列为 47、78、71、99；继续从右向左看，发现 71 比基准值 78 小，进行交换，得到的数列为 47、71、78、99。此时 i 在整体数组中的下标为 6，j 为 5，若继续 j++ 则与 i 相遇，所以完成此轮排序。
此时右边数列的 k 为 6，一般会是相遇的位置，也就是基准值所在的位置，这时数列又被分为两部分，左边是 47、71，右边是 99，需要继续对左边部分的数据进行排序，虽然只有两个数据，但我们还是继续按照快速排序的思想操作一下，选择 47 作为基准数，将i进行从右向左的移动、比较，发现 i 与 j 相等时没有产生移动，完成第 2 轮排序。
至此，所有排序都已经完成，最终数列的结果是 19、24、29、47、47、71、78、99，怎么样，快速排序是不是非常简单地完成了所有的排序呢？虽然本次快速排序没有改变相同值的元素的顺序，但是由于快速排序需要对数列中的元素来回移动，有时还是会改变相对顺序的（比如 47 在第 1 轮的移动过程中就被移动到 47 的右边了），所以快速排序并不是一个稳定的算法。
代码实现：
int[] data = new int[] { 42, 20, 17, 27, 13, 8, 17, 48 };
QuickSort(data, 0, data.Length - 1);
static void QuickSort(int[] dataArray, int left, int right)
{
if (left < right)
{
int x = dataArray[left]; // 基准数，把比他小或者等于他放在他左边，然后把比它大的放在他右边
int i = left;
int j = right; // 用来做循环的标志位
while (true && i < j) // 当i=j的时候，说明找到了一个中间位置，这个中间位置就是基准数所在的位置
{
// 从后往前比较，找到一个比x小或者等于的数字，把他放在基准数位置
while (true && i < j)
{
if (dataArray[j] <= x) // 找到了一个比基准数小于或等于的数字，应该把他放在x的左边
{
dataArray[i] = dataArray[j];
break;
}
else
{
j--; // 向左移动到下一个数字，然后作比较
}
}
// 从前往后找一个比x大的数字，放在新的基准数位置，即j的位置
while (true && i < j)
{
if (dataArray[i] > x)
{
dataArray[j] = dataArray[i];
break;
}
else
{
i++;
}
}
}
// 跳出循环，现在i== j 是中间位置
dataArray[i] = x;
QuickSort(dataArray, left, i - 1);
QuickSort(dataArray,i + 1,right);
}
}
foreach (var temp in data)
{
Console.WriteLine(temp + " ");
}
快速排序的特点及性能
快速排序是在冒泡排序的基础上改进而来的，冒泡排序每次只能交换相邻的两个元素，而快速排序是跳跃式的交换，交换的距离很大，因此总的比较和交换次数少了很多，速度也快了不少。
但是快速排序在最坏情况下的时间复杂度和冒泡排序一样，是 O(n2)，实际上每次比较都需要交换，但是这种情况并不常见。我们可以思考一下如果每次比较都需要交换，那么数列的平均时间复杂度是 O(nlogn)，事实上在大多数时候，排序的速度要快于这个平均时间复杂度。这种算法实际上是一种分治法思想，也就是分而治之，把问题分为一个个的小部分来分别解决，再把结果组合起来。
快速排序只是使用数组原本的空间进行排序，所以所占用的空间应该是常量级的，但是由于每次划分之后是递归调用，所以递归调用在运行的过程中会消耗一定的空间，在一般情况下的空间复杂度为 O(logn)，在最差的情况下，若每次只完成了一个元素，那么空间复杂度为 O(n)。所以我们一般认为快速排序的空间复杂度为 O(logn)。
快速排序是一个不稳定的算法，在经过排序之后，可能会对相同值的元素的相对位置造成改变。
快速排序基本上被认为是相同数量级的所有排序算法中，平均性能最好的。
