java递归算法

什么是递归

递归就是一个程序或函数在其中定义或说明有之间或者间接调用自身的一种方法，它通常把一个大型复杂的问题层层转化为一个原问题相似的规模较小的问题来求解，递归策略只需要少量的程序就可以描述出解题过程所需要的多次重复计算，大大的减少了程序的代码量，递归的能力在于用有限的语句来定义对象的无限集合，一般来说，递归需要边界条件，递归前进段和递归返回段，当边界条件不满足时，递归前进，当边界条件满足时，递归返回。

递归示例

我这里采用的是一个很常见的问题，也是我在知乎上面看到的

• 假设你在一个电影院，你想知道自己坐在哪一排，但是前面人很多，你懒得去数了，于是你问前一排的人「你坐在哪一排？」，这样前面的人 (代号 A) 回答你以后，你就知道自己在哪一排了——只要把 A 的答案加一，就是自己所在的排了，不料 A 比你还懒，他也不想数，于是他也问他前面的人 B「你坐在哪一排？」，这样 A 可以用和你一模一样的步骤知道自己所在的排。然后 B 也如法炮制，直到他们这一串人问到了最前面的一排（或者说问到了知道自己是哪一排的人，预示着调用结束），第一排的人告诉问问题的人「我在第一排」，最后大家就都知道自己在哪一排了

递归算法实例

• 阶乘
  要求给一个数值，计算它的阶乘，例如给的是4 阶乘为432*1

public class DiGui {

    public static int getFactorial(int n) {
        if (n >= 0) {
            if (n == 0) {
                System.out.println(n + "!=1");
                return 1;
            } else {
                System.out.println(n);
                int temp = n * getFactorial(n - 1);
                System.out.println(n + "!=" + temp);
                return temp;
            }
        }
        return -1;
    }

    public static void main(String[] args) {
        getFactorial(4);
    }

}

输出

由下面的图形可以知道详细的过程

getFactorial方法在调用自身的时候，它的参数是4，每次减一，这个方法返回自身，知道减到0，于是方法返回，这样会引发一系列的返回，脱离被放弃的那一层，每当返回时，这个方法把调用它的单数n与其调用的下一层的返回值想乘，注意，在最底层返回之前，实际上是在同一时刻有四个不同的getFactorial方法实例存在，最外层是4，最里面的是1

递归的二分查找

首先二维数组一定是有序的，
在有序的数组array[]中，不断地将中间值（mid）和被查找的值比较，如果被查找的值等于affay[],就返回下标array[mid]，否则就像查找的范围缩小一半，如果被查找的小于array【mid】,就继续查找左边得值，如果查找大于array【mid】就向右边查找，直到查找为空,查找结束!
详细代码请查看我的这一篇博客
https://blog.csdn.net/qq_40688338/article/details/84557959

分治算法

当我们求解某些问题，由于这些问题要处理的数据相当多，或求解的方式比较复杂，使得直接求解在时间上相当长，或者直接无法求出，对于这类问题，我们往往把它分成几个子问题，找到求出这个子问题的解法后，再找到合适问题的解法，如果这些子问题还较大，难以解决，我们可以把它再分成介个更小的子问题，以此类推，直到找到解法为止，这就是分治解法的基本思想。
上面所说的递归的二分查找就是一个分治算法的经典例子，分治算法常常是一个方法，在这个方法中含有两个对自身的递归调用，分别对应于问题的两个部分，
二分查找中，将查找范围分成比查找值大的一部分和比查找值较小的一部分，每次递归只有一部分执行。

汉诺塔问题

汉诺塔问题是由很多放置在三个塔座上的盘子组成的一个古老的难题，如下图所示，所有的盘子的直径是不同的。并且盘子中央都有一个洞使得它刚好可以放在塔座上，所有的盘子刚开始都是在a座上，这个难题的目标是将左右的盘子都从塔座a，移到塔座c上，每次只可以移动一个盘子，并且任何一个盘子都不可以放置在比它小的盘子上，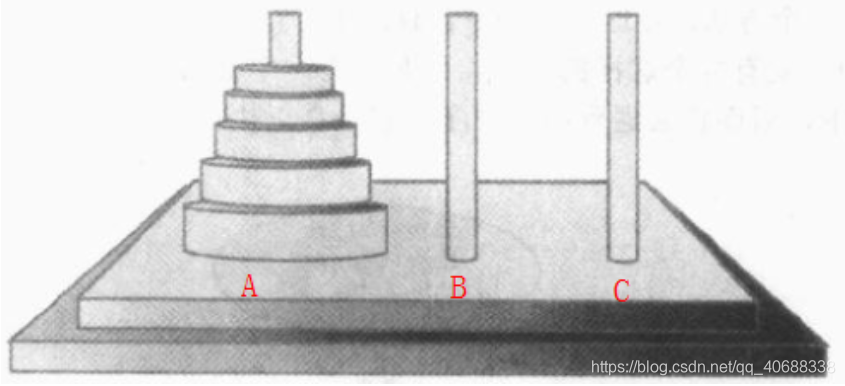
这个问题可以先从简单的方面想，然后一步一步出发，假设有2个盘子，盘子的大小我按照阿拉伯数字命名。从小到大，如果a上面有两个盘子，分别是1,2那么我们只需要把1的盘子移到b上面，然后把2的盘子移到c上面，最后把b上面的盘子1移动到c上面就可以了，这样两个盘子的问题就解决了，
如果是三个盘子呢？我们一样的来命名1,2,3，假设先把1的盘子移动到c的上面，然后把2的盘子移动到b上面，这样目前就是a上面的是3，b上面的是2，c上面的是1，然后将c上面的盘子移动到b上面，继续把a的盘子移动到c上面，这样的话，目前就是b上面有1,2，c上面的有3，现在答案已经很清楚了，将b上面的盘子移动到a上面，然后第二个盘子移动到c上面，最后a的盘子移动到c上面，这样问题就解决了，
但是如果有四个，五个，n个盘子呢？这个时候递归的思想就很好的解决这样的问题了，当只有两个盘子的时候，我们只需要将b塔座作为中介，将盘子1放到中介b上面，然后将盘子2放到c上面，最后将b上面的盘子1移动到c盘就可以了

所以无论多少盘子，我们都将其看做只有两个盘子，假设n个盘子在a的上面，我们将其看做只有两个盘子，只有（n-1）和n这两个盘子，

• 先将a上面的n-1的哪一个盘子放到塔座b上面，然后将第n的盘子放到目标塔上面，
• 然后a的上面为空，看做中间塔，b上面的有n-1个盘子，将第n-2以下的盘子看成一个盘子，放到中间a塔上面，然后将第n-1的盘子放到c上面，
• 这是发现a上面有n-2个盘子，b上面为空，按照上面的方式以此类推，直到全部放到冰箱里面

简单的来说

1. 从初始塔a上移动到包含n-1个盘子到c上面
2. 将a上面剩下的一个盘子，放到c上面
3. 然后假设b上面有n-1个盘子，然后将它看成为n继续将看成n的盘子中间的n-1个盘子放到a上面
4. 将b上面剩下的那个盘子放到c上面。
5. …

 public static void main(String[] args) {
//        getFactorial(4);
        move(4,"A","B","C");
    }

    /**
     * 汉诺塔问题
     *
     * @param dish 盘子个数(也表示名称)
     * @param from 初始塔座
     * @param temp 中介塔座
     * @param to   目标塔座
     */
    public static void move(int dish, String from, String temp, String to) {
      if (dish == 1) {//圆盘只有一个的时候 将其从a移动到c
            System.out.println("将盘子" + dish + "从塔座" + from + "移动到目标塔座" + to);
        }else {
            move(dish-1,from,to,temp);//a为初始塔座，b为目标塔座，c为中介塔座
            System.out.println("将盘子"+dish+"从塔座"+from+"移动到目标"+to);//把a上面的最下面的一个盘子移到c上面
            move(dish-1,temp,from,to);//b为初始塔座，c为目标塔座，a为中介塔座
        }
    }

 

输出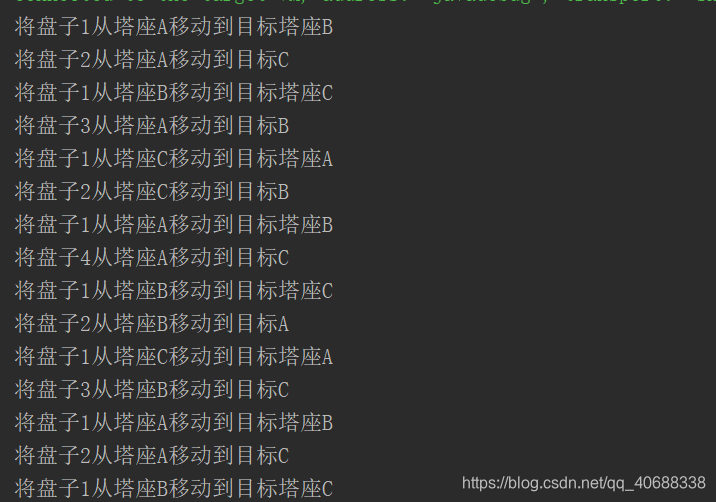

归并排序

归并排序算法的中心是归并两个已经有序的数组，归并两个有序的数组a和b，就生成了第三个有序的数组c，数组就是包含数组a和数组b的所有数据项，同时该算法采用经典的分治策略

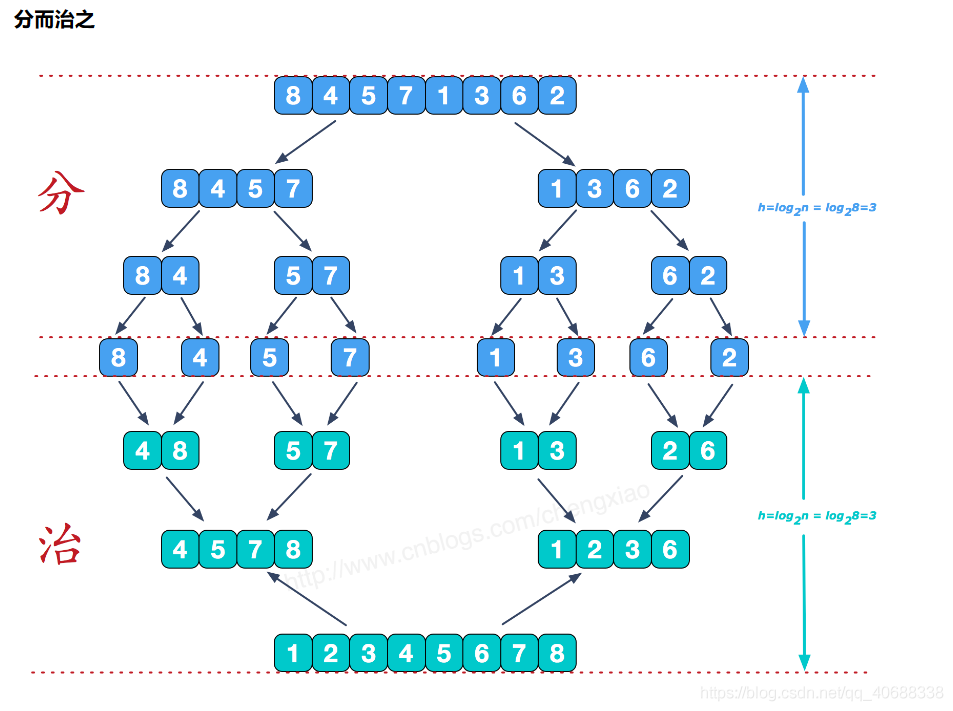
未使用递归算法

    public static void main(String[] args) {
//        getFactorial(4);
//        move(4,"A","B","C");
        int[] array = {11, 22, 33, 44, 55, 66, 77, 88, 99, 100, 104};
        int[] arrayB = {1, 21, 41, 51, 61, 71, 81, 91};
        int[] arrayC = new int[19];
        merge(array,arrayB,arrayC);
        display(arrayC);
    }

    /**
     * @param arrayA 数组a
     * @param arrayB 数组B
     * @param arrayC 数组C
     */
    public static void merge(int[] arrayA,
                             int[] arrayB,
                             int[] arrayC) {
        int a = 0;
        int b = 0;
        int c = 0;
        while (a < arrayA.length && b < arrayB.length) {//当a和b都有数据数才执行
            if (arrayA[a] < arrayB[b]) {//当a的数小于b的数时
                arrayC[c++] = arrayA[a++];//将a的数添加到c中并且下标加1
            } else {
                arrayC[c++] = arrayB[b++];//将b中的数添加到c中并且下标加一
            }
        }
        //走到这一步的时候要么是a中没有数或者是b中没有数
        while (a < arrayA.length) {
            arrayC[c++] = arrayA[a++];//如果A中存在则将剩下的数添加到c中
        }
        while (b < arrayB.length) {
            arrayC[c++] = arrayA[b++];//如果b中的数存在则先加到c中
        }

    }

    /**
     * 排序
     */

    public static void display(int[] array) {
        for (int j = 0; j < array.length; j++) {
            System.out.print(array[j] + ",");

        }
    }

 

输出

详细的步骤我在代码上面已经写下来了

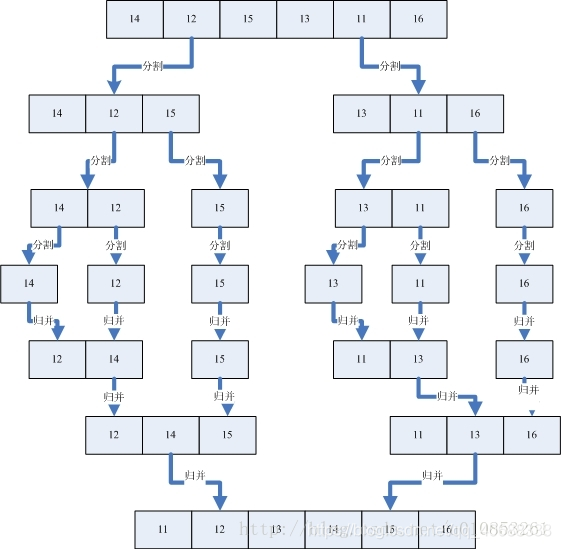
递归排序

• 先将数组分成两半
• 再把每一半分成两个1/4,
• 继续把1/4分解成1/8依次类推
• 直到分割成一个一个的数组，再把这些数据归并到一起直到有序
  

public static void main(String[] args) {

        int[] arr = {12, 41, 2, 3, 6, 54, 15, 21, 41, 85, 94, 12, 46};
        arr = merSort(arr, 0, arr.length - 1);
        System.out.println(Arrays.toString(arr));
    }

    public static int[] merSort(int[] arr, int start, int last) {
        if (last > start) {
            //也可以是(start+last)/2，这样写是为了防止数组长度很大造成两者相加超过int范围，导致溢出
            int mid = start + (last - start) / 2;
            merSort(arr, start, mid);//左边数组的排序
            merSort(arr, last, mid);//右边数组的排序
            merge(arr, start, mid, last);
        }
        return arr;
    }

    public static void merge(int[] arr, int start, int mid, int last) {
        int[] temp = new int[last - start + 1];//临时定义的数组

        int i = start;//定义左边数组的下标
        int j = mid + 1;//定义右边数组的下标
        int k = 0;
        while (i <= mid && j <= last) {
            if (arr[i] < arr[j]) {
                temp[k++] = arr[i++];
            } else {
                temp[k++] = arr[j++];
            }

        }
        //            把左边的数移动到新的数组
        while (i <= mid) {
            temp[k++] = arr[i++];
        }
//        把右边的数移动到新的数组中
        while (j <= last) {
            temp[k++] = arr[j++];
        }
//        把新数组中的数覆盖到arr中
        for (int a = 0; a < temp.length; a++) {
            arr[a + start] = temp[a];
        }
    }

 

输出

归并排序的效率是比较高的，设数列长为N，将数列分开成小数列一共要logN步，每步都是一个合并有序数列的过程，时间复杂度可以记为O(N)，故一共为O(NlogN)。因为归并排序每次都是在相邻的数据中进行操作，所以归并排序在O(NlogN)的几种排序方法（快速排序，归并排序，希尔排序，堆排序）也是效率比较高的。