校招基础——时序分析计算

 

1、如图所示时序路径示意图，椭圆表示组合逻辑，FF1，FF2表示寄存器，A表示数据输入端口，CLK表示时钟输入端口，Z表示数据输出端口（C）

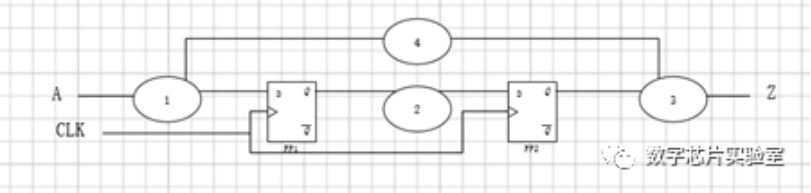
A.只要在端口CLK上创建时钟，即可约束A->Z之间的组合逻辑的延时。

B. 只要在端口Z上设置输出延时，即可约束FF2 -> Z之间的组合逻辑的延时。

C. 只要在端口CLK上创建时钟，即可约束FF1->FF2之间的组合逻辑的延时

D. 只要在端口A上设置输入延时，即可约束A->FF1之间的组合逻辑的延时

 

2、时钟周期为T，触发器D1时钟沿到来至触发器输出Q变化的时间为Tco（clk~Q）最大为T1max，最小为T1min，逻辑组合电路的延迟时间最大为T2max,最小为T2min，问触发器D2的建立时间和保持时间应满足什么条件。

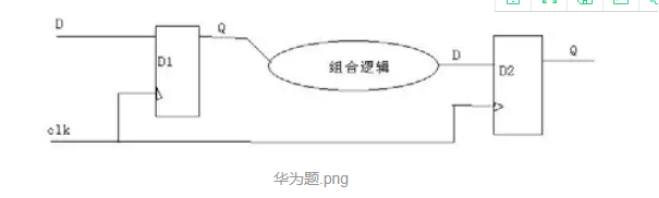
解：其他数据都没给，所以不带入，只带入题目给了的数据。

T2 setup < T-T1max -T2max（setup找最小，自然选max）

T2hold < T1min + T2min（hold找最小，自然选min）

 

3、已知reg的setup，hold时间，求中间组合逻辑的delay范围。

解：Delay < period -setup-hold

 

4、如何计算周期T与设计频率（最大频率）Fmax。

Tclk = TCKO + TLOGIC+TNET+TSETUP-（TCD2-TCD1）

FMAX=1/TCLK

 

5、请计算下面逻辑中时钟clk可以达到的最小周期。（图中0.8/0.65/0.6分别为CT1、CT2、CT3的器件延时），3.8为CK1经过combinational logic到达DL2的D端上的传播延时、0.2为D触发器建立时间。

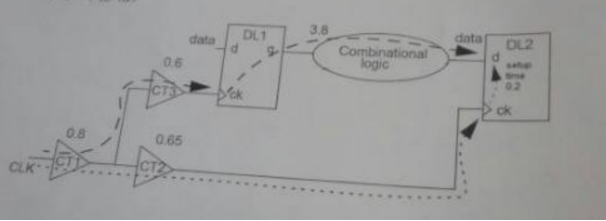
解：Tmin =（Tco + Tdata）+Tsu-Tskew

= 3.8 + 0.2-（0.65-0.6）=4-0.05=3.95

 

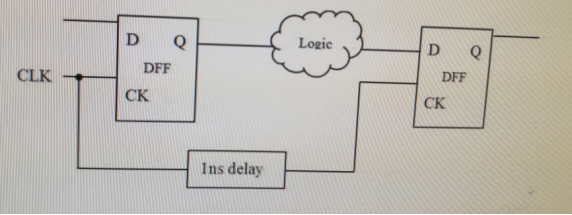
6、如下图，有一同步电路，module A有一个信号A输出给module B。时钟周期是2ns，DFF的setup time 为0.2ns，hold time为0.18ns，DFF的clk端延时为0.12ns，D1=0.6ns。考虑clock skew = 0.05ns，计算D2的最大值为多少？

 

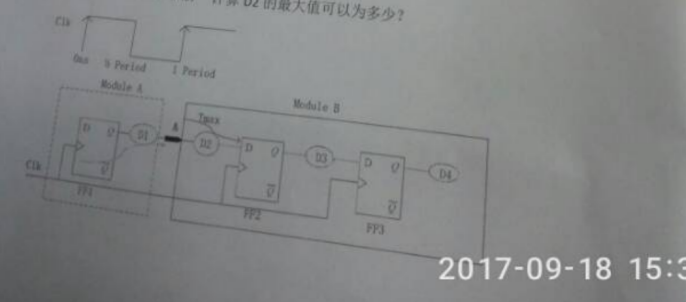
解：建立裕量：Tcyc + Tskew-(Tsu+Tco+Tdata) > 0

2 + 0.05 - (0.2+0.6+Tdata)>0

Tdata < 1.25

所以最大值为1.25ns。

 

7、如下图所示，假定反向器的最大/最小延迟分别为Tinv_max/Tinv_min，与门的最大/最小传输延迟时间分别为Tand_max/Tand_min，寄存器（DFF）的时序参数分别是：建立时间（Tsu），保持时间（Thold）和传输时间（Tpd）。

（1）请解释寄存器（DFF）的3个典型的时序

 

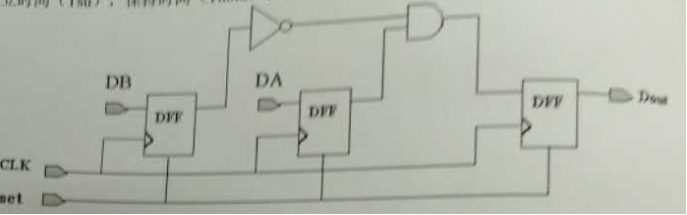
建立时间Tsu：在触发器的时钟上升沿到来之前，数据保持稳定不变的时间。

保持时间Th：在触发器的时钟上升沿到来之后，数据保持稳定不变的时间。

Tpd:当时钟有效沿变换后，数据从输入端到输出端的最小时间间隔。

（2）基于上述电路所给的参数，请分析该电路能正常工作的最大频率。如果需要的未给定的参数，请给自行定义并说明。

Tmin = Tco+Tsu+Tdata-Tskew

Fmax=1/（Tco+Tsu+Tdata-Tskew）=1/（Tpd+Tsu+Tand_min）这里没有给出Tskew，所以不管他。

（3）请在图上表示可能的时序关键路径，并列举至少两种可能的方法来改善其数据路径的延时。

关键路径：通常是指同步逻辑电路中，组合逻辑延时的最大的路径。也就是说关键路径是对设计性能起决定性作用的时序路径。所以从图上找组合逻辑最长的那一条。

对同步逻辑常用的时序优化方法包括（1）插入寄存器（2）并行化设计（3）逻辑展平（4）均衡设计（5）优化路径

 

8、下图是某电路中的一条关键路径，其中DFF的参数如下：tco=1ns，tsu=2ns，thold = 1ns,Logic的最大延时为4ns,最小延时为3ns，clk的jitter为2ns，则电路最小的时钟周期为（A）

 

A、7ns B、8ns C、9ns D、

解：Tmin=Tco+Tdata+Tsu-Tskew+Tjitter = 1+3+2-1+2=7ns（注意，题目没给Tskew，但图上画出来了。）

我觉得还算按最坏情况算，即取4ns，答案为8ns。

 

9、如下图为某同步电路，DFF1和DFF2的setup，hold和output delay（clk->Q）时间为0.6，0.3，1.2（各时间参数均为ns），假设clk时钟频率为250MHZ，请问DFF2的setup时间和hold时间是否满足并说明其原因。

 

由题意可知：Tcyc=1/250M=4ns，

建立时间：Tcyc + Tskew -Tco - Tdata-Tsu = 4 + (0.8-1)-1.2-2.2-0.6=4-0.2-4=-0.2 <0，违例

保持时间：Tco+Tdata-Tskew-Th = 1.2+2.2-（0.8-1）-0.3=3.4-0.1=3.3，满足

 

10、已知Tsetup=1ns、Thold=1ns、Tclk->q = 1ns。请回答以下问题。

（1）假设存在positive clock skew为1ns，问最高时钟频率为多少？

（2）能容忍的最大positive clock skew为多少？（DFF2的clock比DFF1晚）

（3）能容忍的最大negative clock skew为多少？（DFF2的clock比DFF1早）

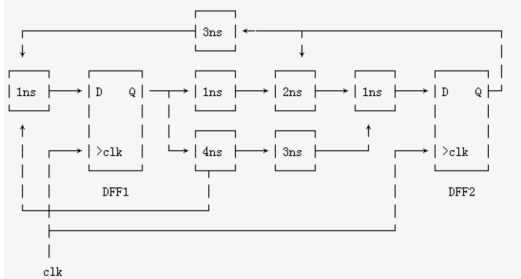
解：（1）5条路径依次分析：Tcyc >= Tco+Tdata+Tsu-Tskew

DFF1->DFF2：1+（4+3+1）+1-1=9ns

DFF1->DFF2：1+（1+2+1）+1-1=5ns

DFF2->DFF1：1+（3+1）+1+1=7ns（这是一个负的Tskew）

DFF1->DFF1：1+（4+1）+1 = 7ns（DFF1到DFF1的时钟不存在Tskew）

DFF2->DFF2：1+（2+1）+1 = 5ns（DFF2到DFF2的时钟不存在Tskew）

最高时钟周期为9ns，所以最高时钟频率是1/9ns。

（2）公式Th <= Tco + Tdata - Tskew，即Tskew <= Tco + Tdata - Th，路径代入可得答案。

DFF1->DFF2：1+（4+3+1）-1=8ns

DFF1->DFF2：1+（1+2+1）-1=4ns

DFF2->DFF1：-（1+（3+1）-1）=-4ns（这是一个负的Tskew）

DFF1->DFF1：0ns（DFF1到DFF1的时钟不存在Tskew）

DFF2->DFF2：0ns（DFF2到DFF2的时钟不存在Tskew）

出现一个负的Tskew，这是不能取的，因此最大positive clock skew答案为4ns

（3）和（2）类似，但是答案取反，因此最大negative clock skew为4ns。