动态系统的建模与分析

1.解决控制系统问题的思路：

　　a. 被控系统的物理分析、动态表现，在此基础上数学建模；（动力、热力、流体、经济）

　　b. 控制器设计；传统、PID、非线性、自适应、最佳控制；

　　c. 测试；仿真平台、模型样机或真实设备；实验设计；数据采集；校准

　　d. 不断地把测试结果与建立的模型进行比较，验证与修改模型

　　不管是复杂的如自动驾驶，还是简单的如烤箱温度控制，都离不开这样的分析；

　　动态系统的建模与分析是工作的基础，后续的工作都将在这上面完成；

　　一个准确的数学模型对系统动态响应的把握至关重要。

　　e. 模型分电力、流体、热力学、机械系统；

　　f. 拉普拉斯变换 + 微分方程 是表现系统动态响应的基本方法

　　g. 时域分析

　　h. 频域分析

2. 电路系统建模

　　a. 电阻、电容、电感元件上，电压与电流的关系

　　b. KVL定律

　　c. 联立两式

3. 流体跳过

4. 拉普拉斯变换，传递函数，微分方程

　　a. 分析电路的变化，本质上是求解微分方程的过程

　　b. 输入与系统的卷积，结果就是输出

　　c. 计算涉及到了微分、卷积，计算分析不直观，通过拉普拉斯变换，把微分方程转为代数方程，卷积运算变成乘法运算

　　e. 原函数与拉氏变换后的图：

　　

 

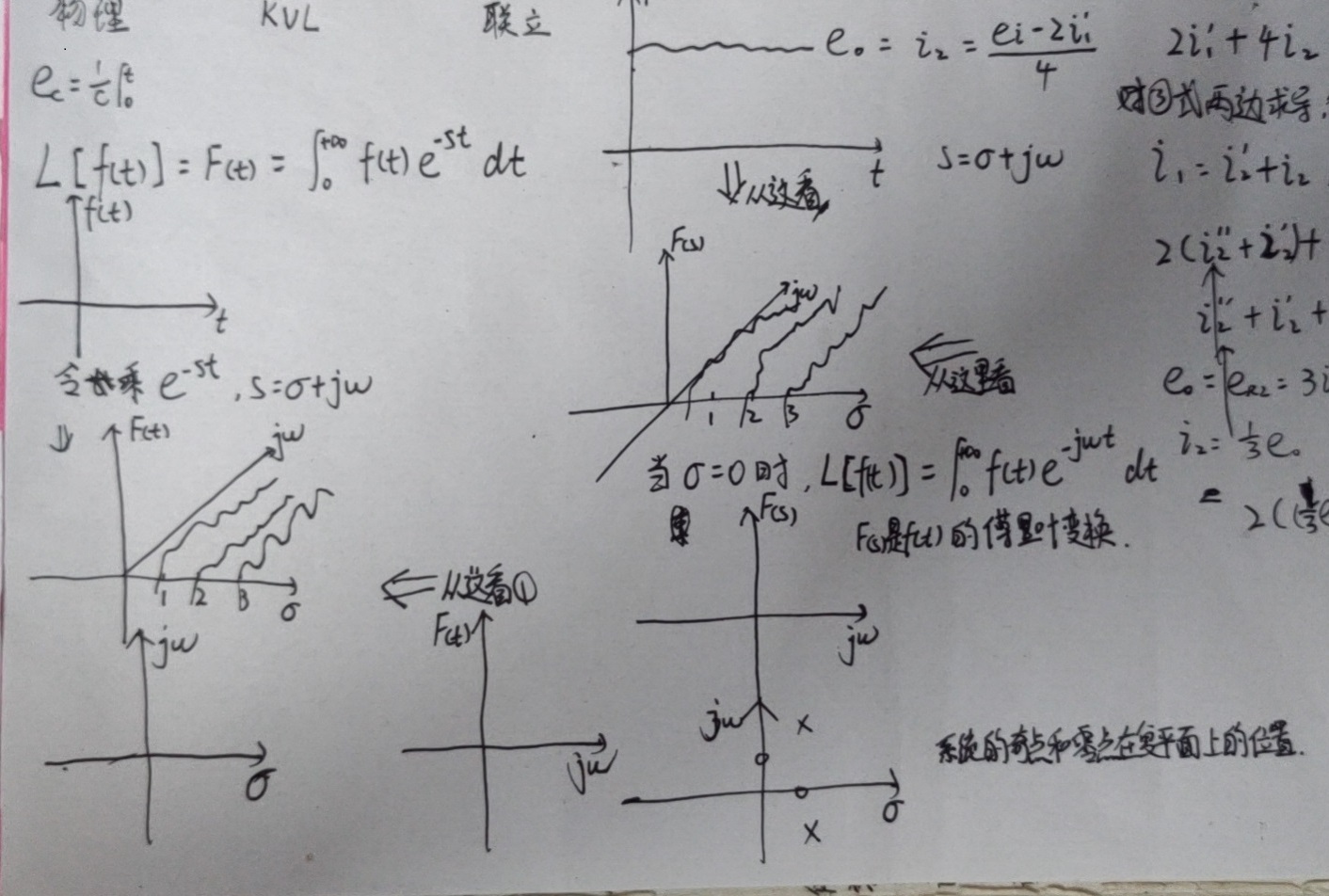
　　f. 指数函数的拉式变化：

　　 

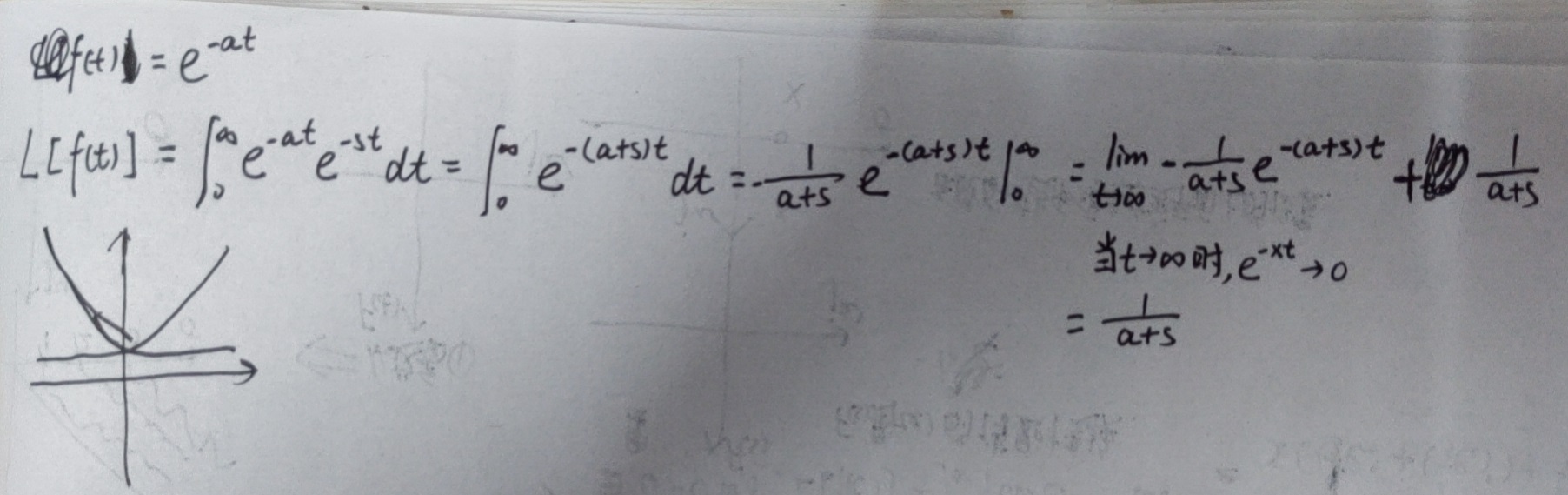
　　g. 正弦函数的拉氏变换：

　　

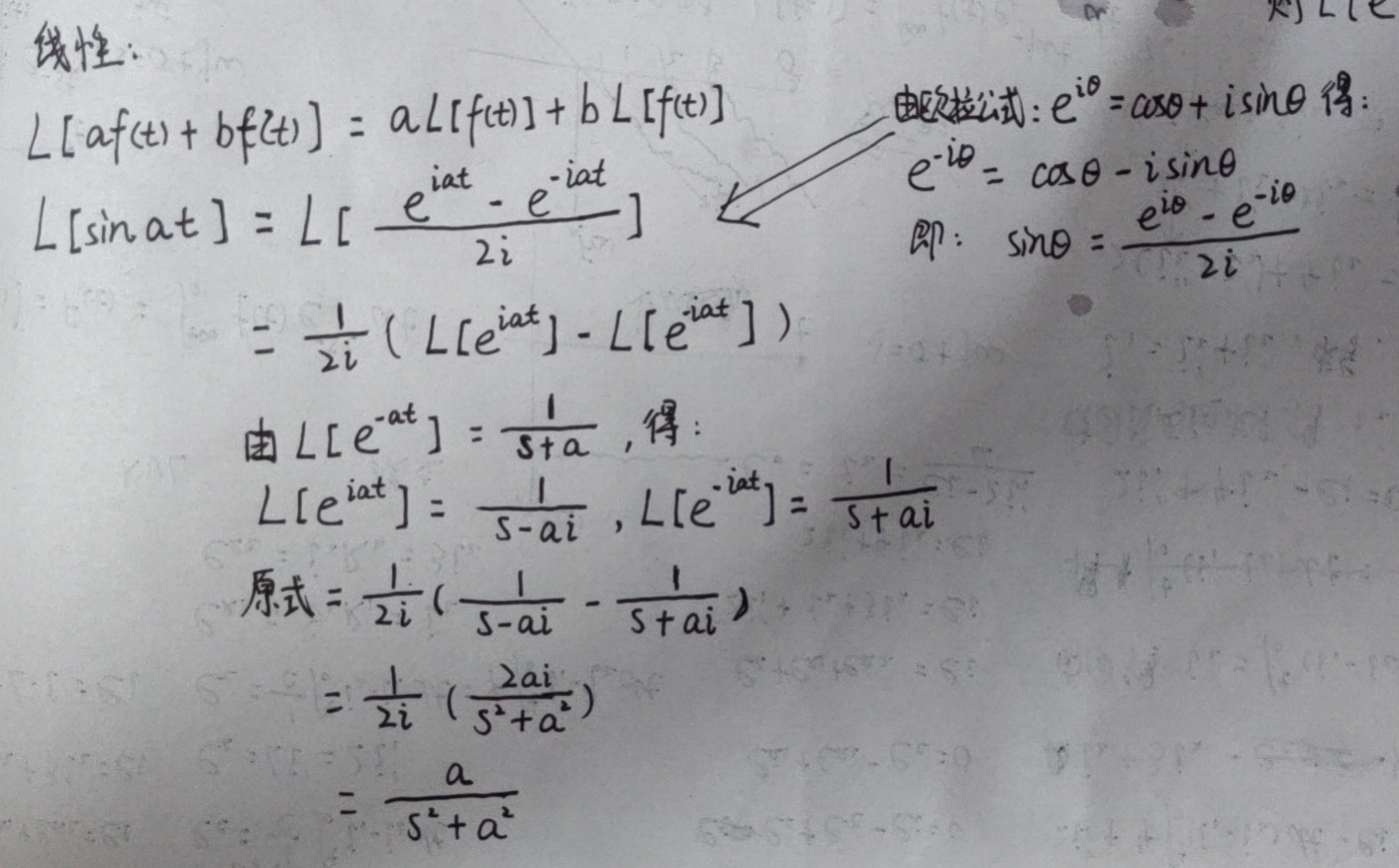
　　h. 运用到电路中：

　　

Tip：之前我很难理解，或者说不能接收，为什么输出和频率扯上了关系，

现在回过头看，学习的角度不同，如果是抱着负担的心态去学理论，很难接受；

如果急需一种思路、思想、理论，来解释、解决我遇到的现实问题，那么我就能让自己去接受，

能接受会改变自己以往观念的理论。所以说学习是一个用已证明理论，来改变已有观念的过程。 

要知道，一直以来，我做的更多的是了解、认知，而不是创造。（加油）

 

5. 拉氏变换的收敛域（ROC）与逆变换

　　a. 收敛域

　　

　　b. 指数函数的拉氏逆变换

 　　

 

 

6. 传递函数与拉氏变换

　　a. 对后面的学习有很大帮助，经典控制如根轨迹、伯德图、信号处理

　　b. 流体物理式子的拉氏变换：

　　

　　c.  当输入为常数时，拉氏变换与逆变换：
　　

　　d. 发现指数是使函数图像收敛的关键，引出极点，经典控制理论的理念

　　

 

7. 一阶系统的单位阶跃响应

 　　a. 对单位阶跃做拉氏变换，作为系统的输入；

　　　　输入 乘 典型一阶系统的传递函数；

　　　　得到输出的 拉氏变换；

　　　　对输出的拉氏变换做逆变换；

　　　　得到在时域上的输出函数，和图像；

　　　　

 

　　　b. 一阶系统时间常数的概念

　　　

 

 　　c. 由时间常数和阶跃响应，测一阶系统的系统特性

　　

 

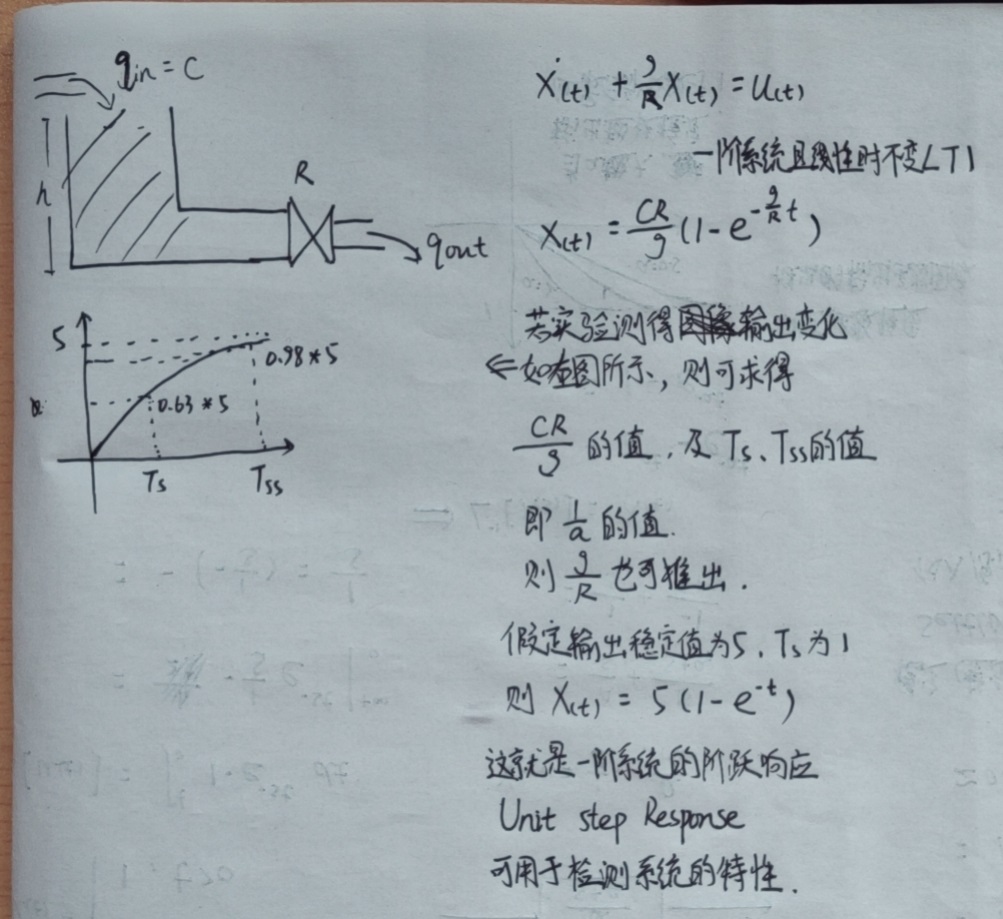
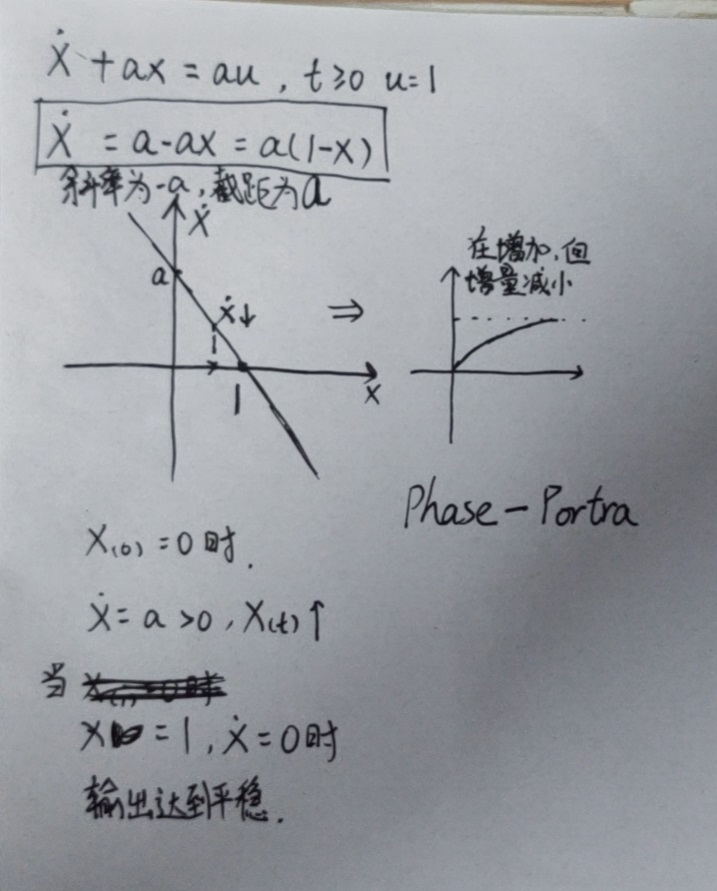
7.5 换个角度分析单位阶跃响应

　　 

 

8. 三角函数化简，多极点系统稳定

 　　

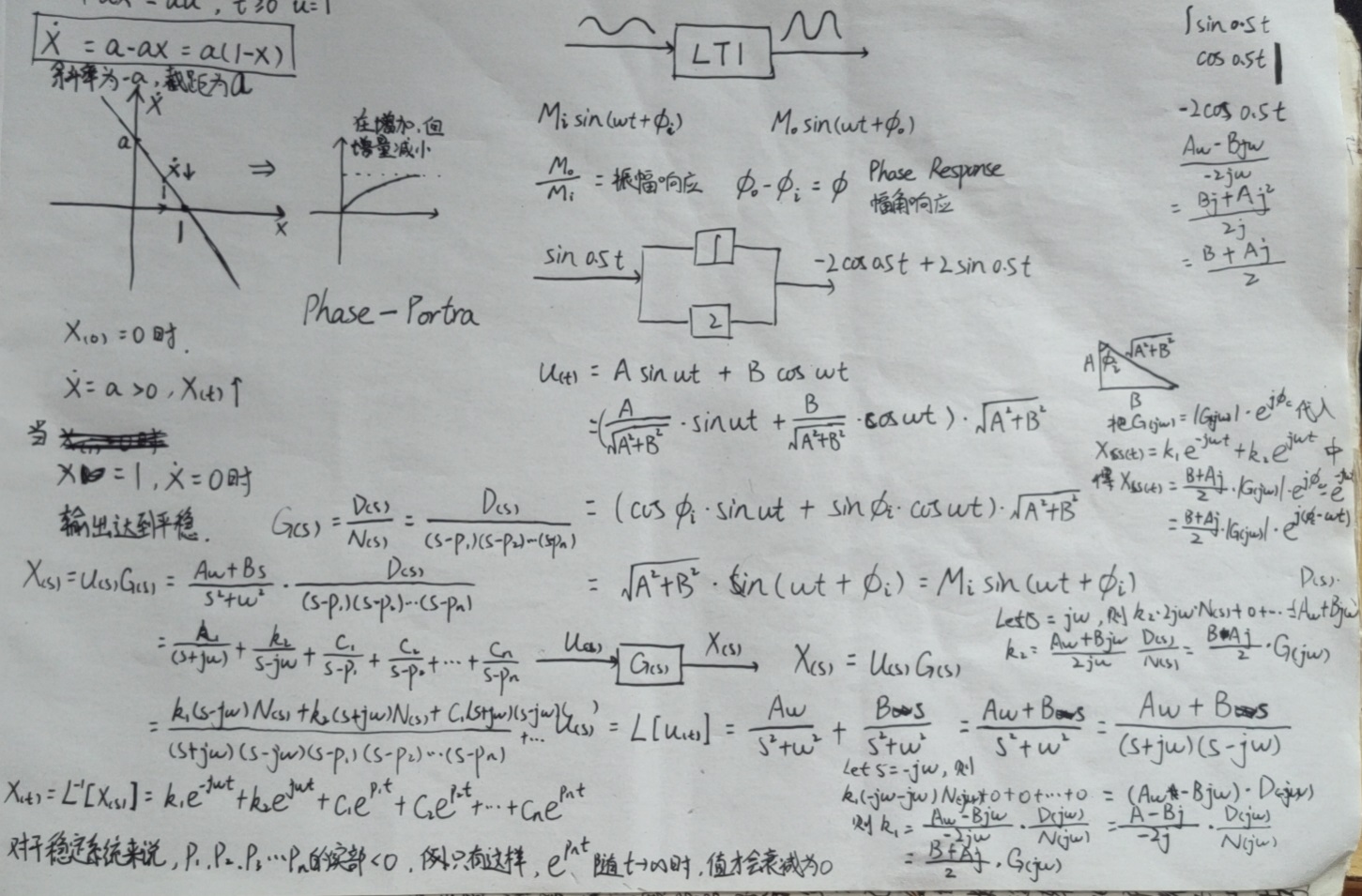
 　　sin函数的频率响应

　　 

 

9. 一阶系统的频率响应

 　　

　　

 

 　　

 

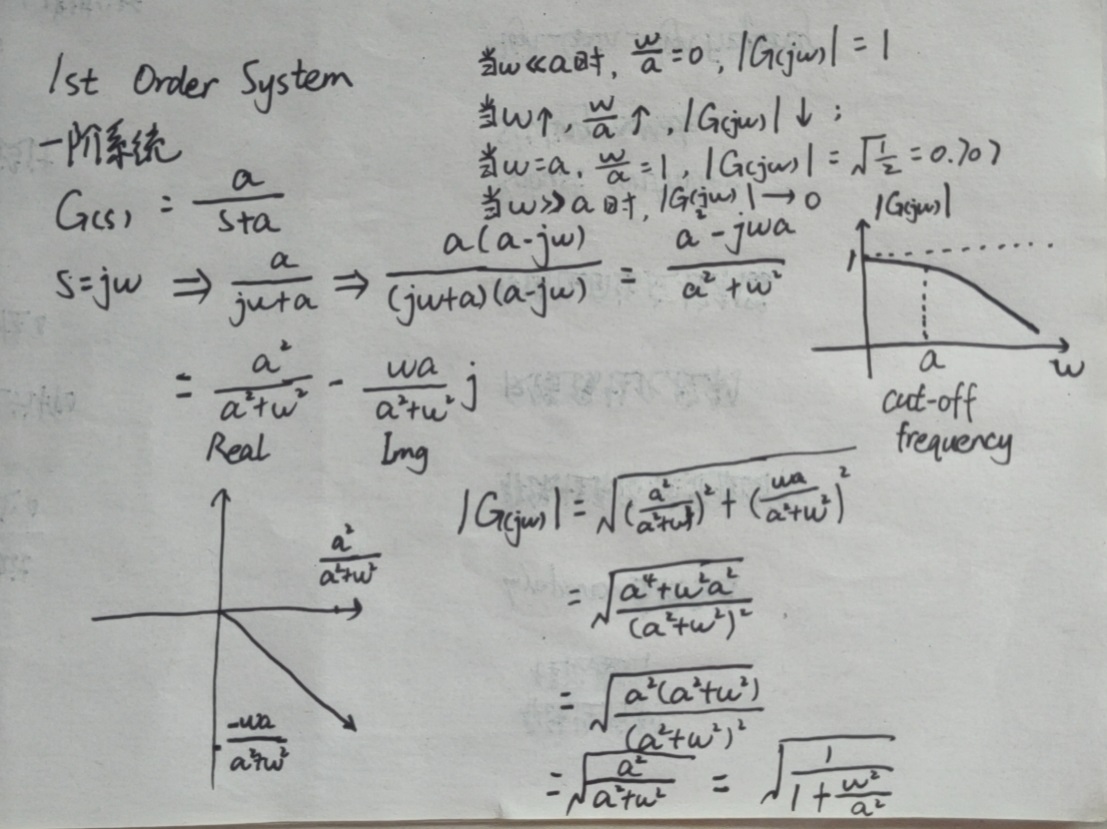
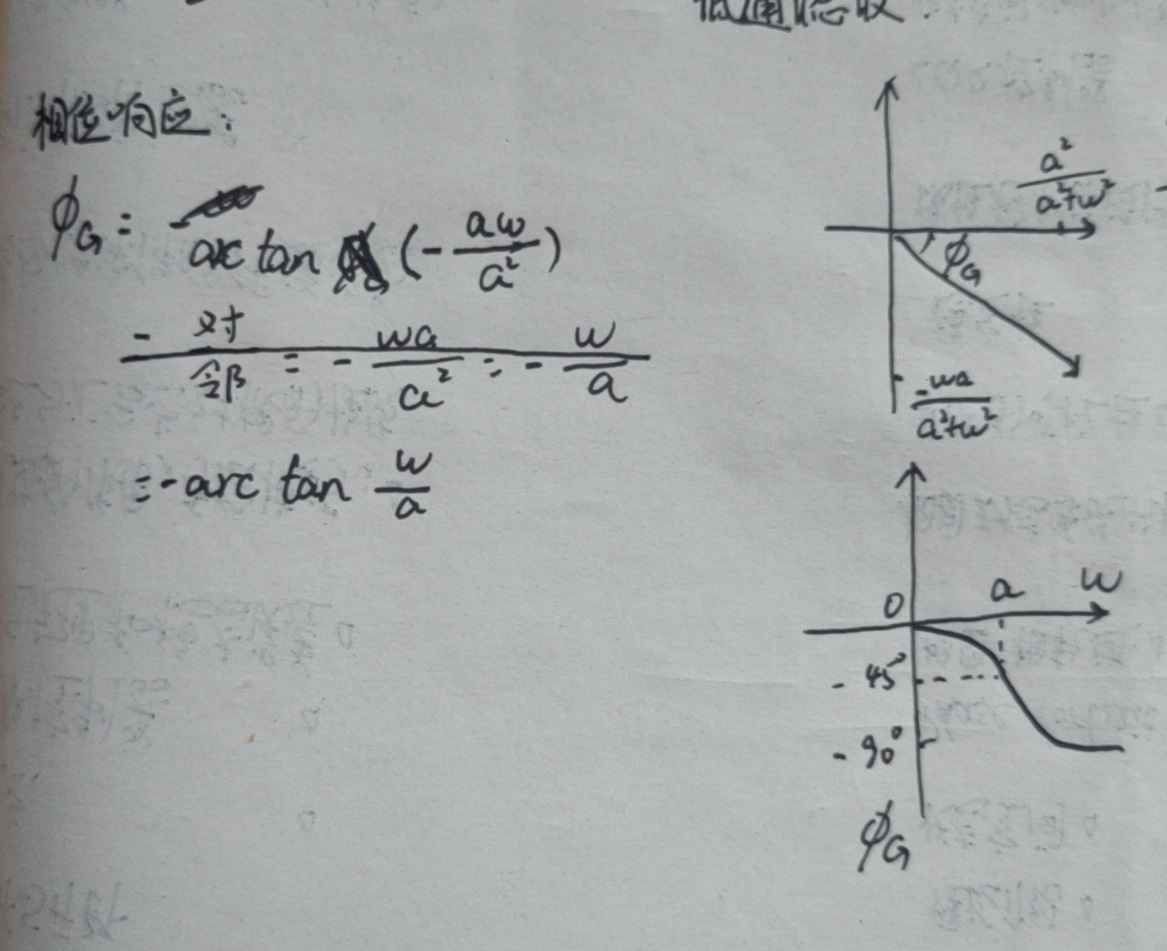
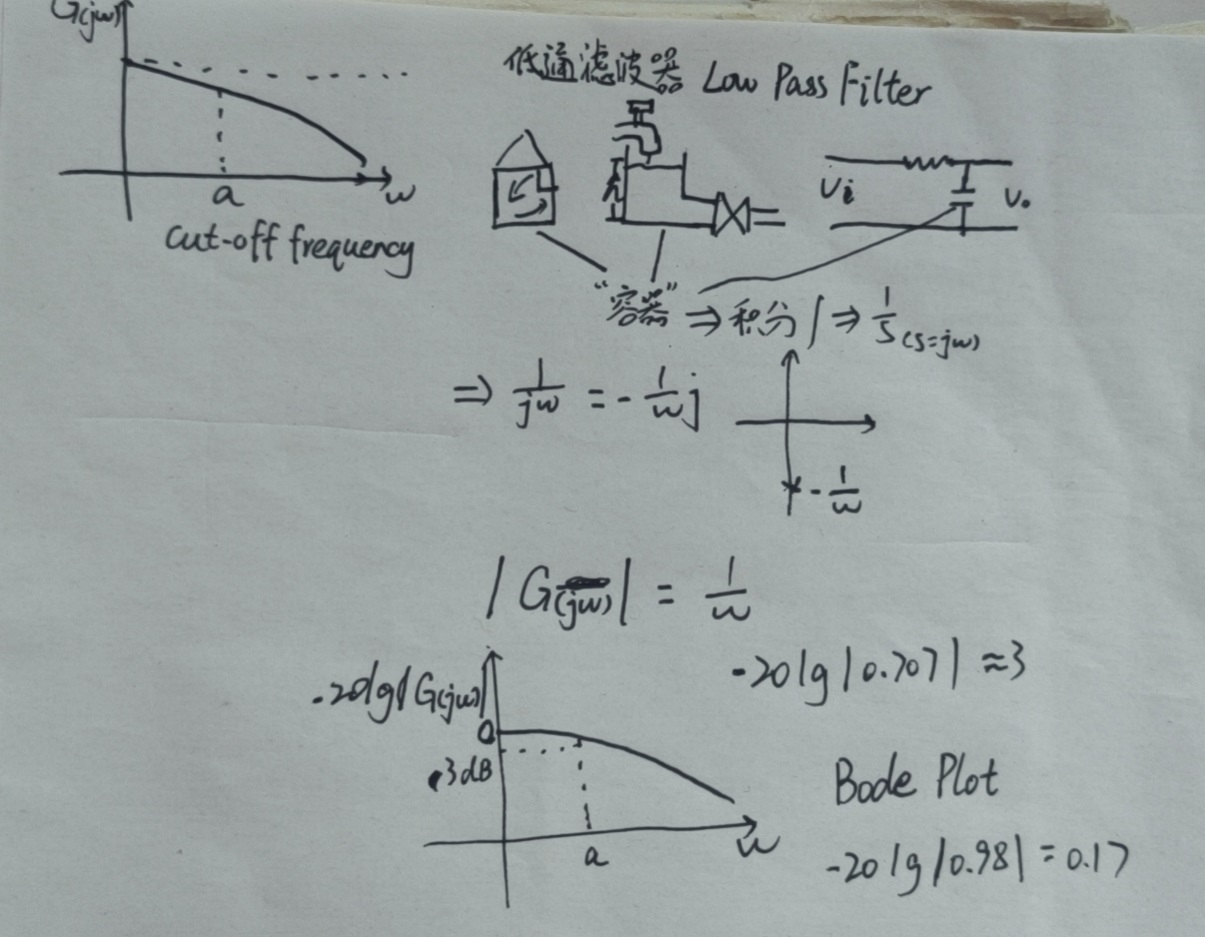
Tips：

PID调参的过程应该是在人工测合适的控制器参数

从上面学到的方法知道，用已知输入，给系统，记录实际输出，以此建立大致的系统模型

但仅限于一阶系统。

我想知道实际系统是几阶？它们对应的数学建模方法又是什么？

 

10. 二阶系统对初始条件的响应

　　　　

　　　　弹簧类成比例（位移），阻尼类成一阶微分（速度），合外力成二阶微分（加速度）；

　　

 

 

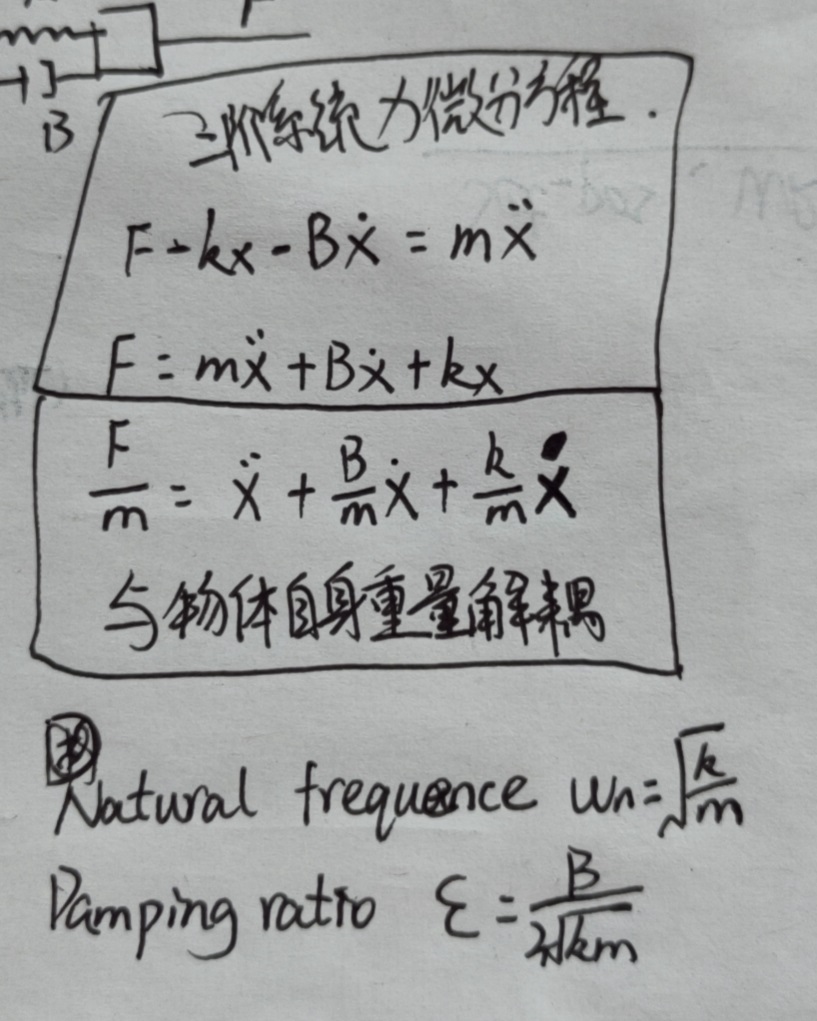
　　zeta > 1时：

　　

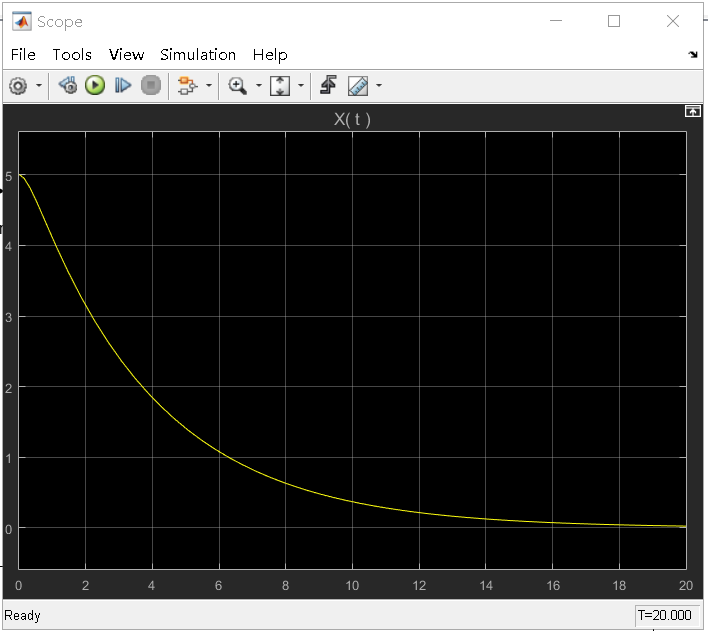
　　zeta = 1:

　　

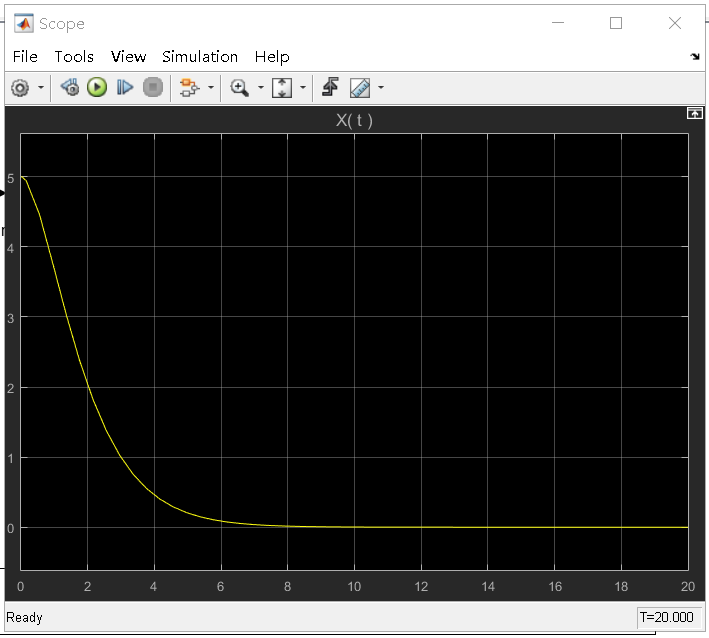
　　zeta < 1:
　　

 

 　　

 

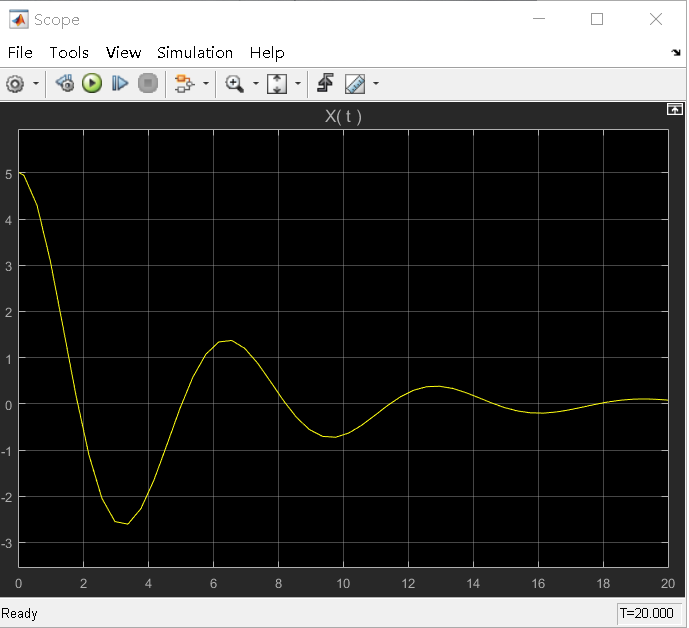
 　　zeta = 0:

　　

　　

 

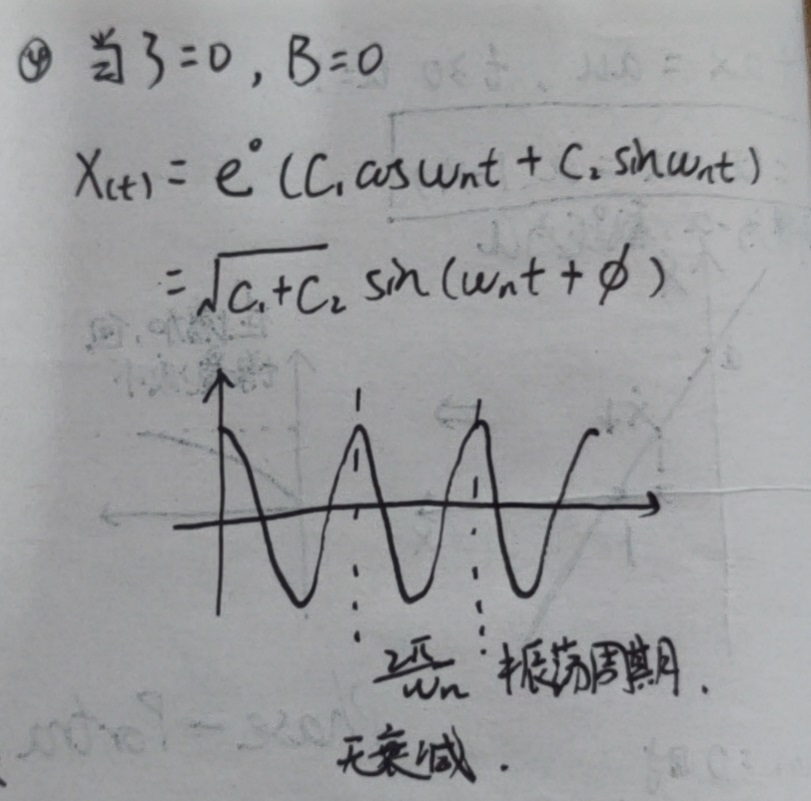
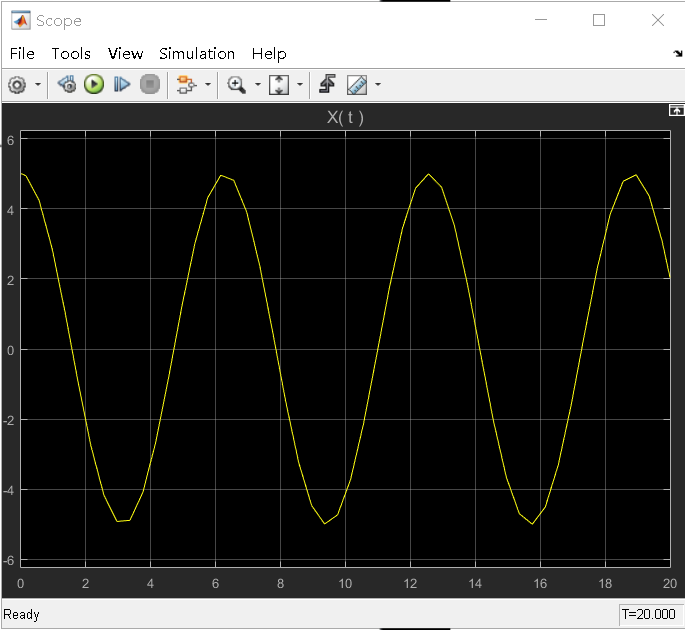
 　　-1 < zeta < 0; 　　zeta < -1 :

　　

 

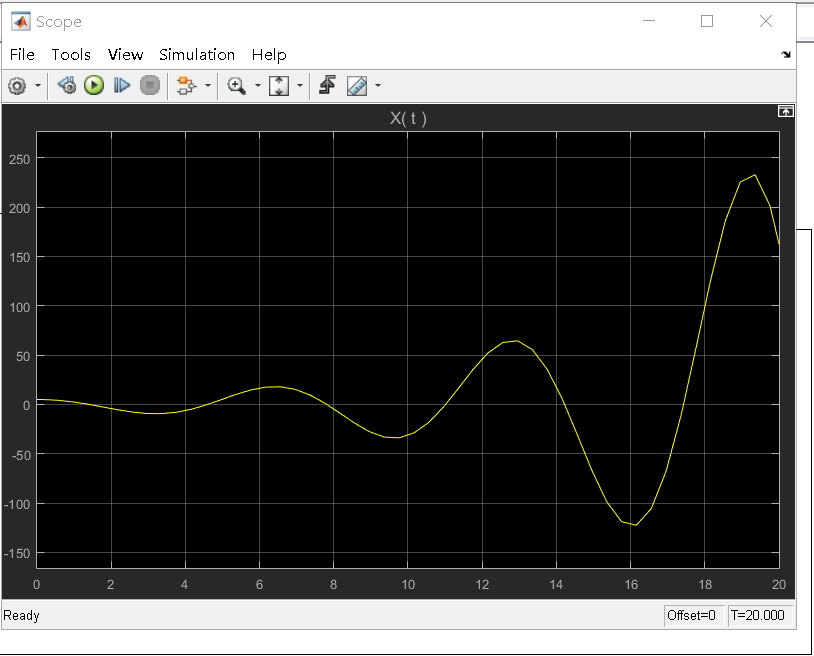
11. 二阶系统的单位阶跃响应

 　　

 

12. 二阶系统的性能分析与比较

 　　

 

 　　

 

 

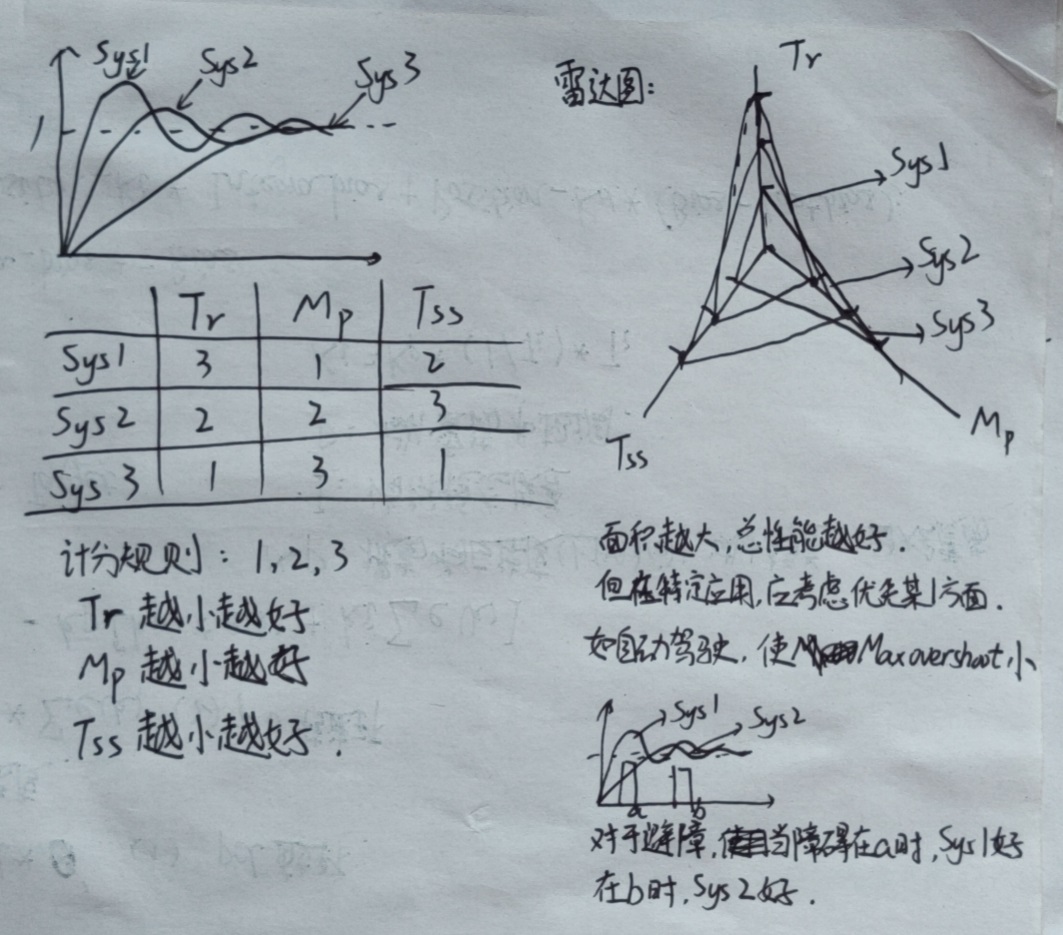
13. 共振现象、二阶系统频率响应

 　　

 

 

14.  二阶系统频率响应（数学推导）

 　　

 

 　　

 

15.  伯德图

 　　

 

 　　

　　

 

 　　

 

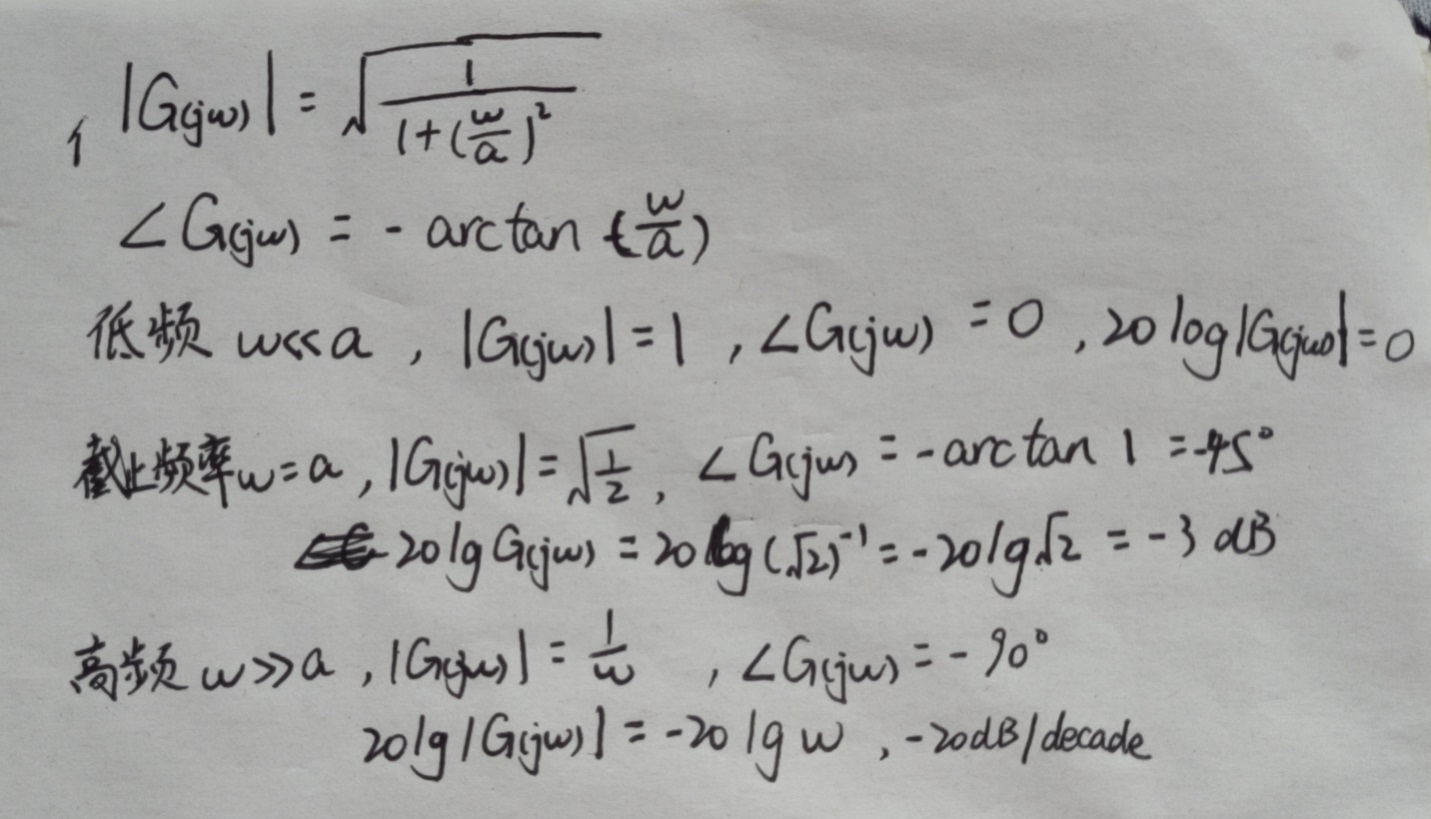
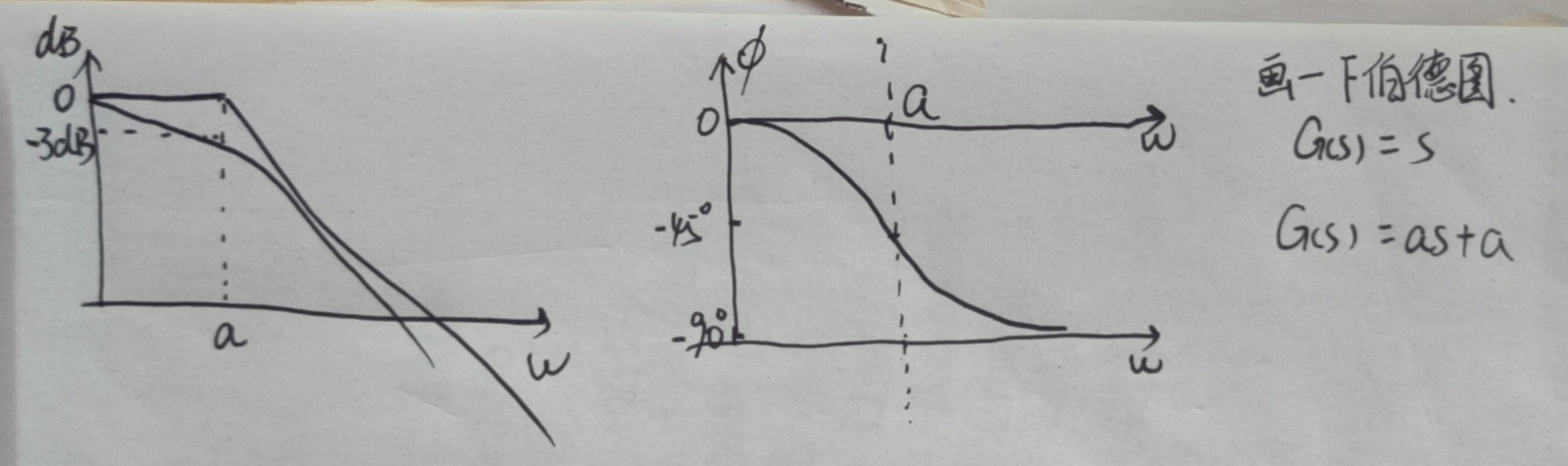
 　　bode([0 1],[1 1])

　　

 

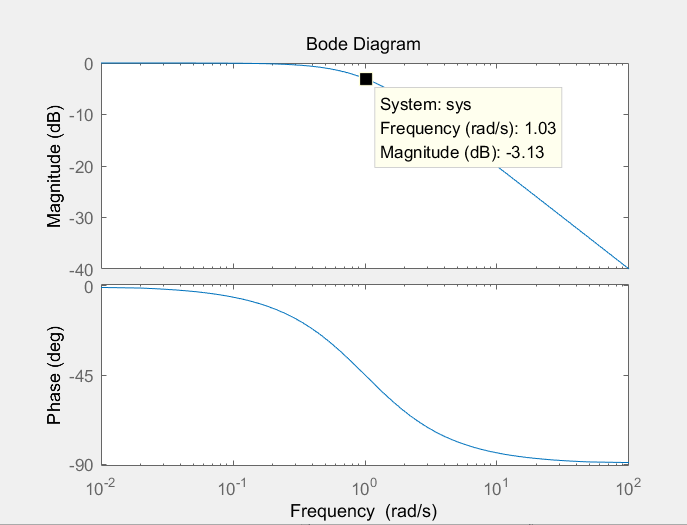
 　　bode([0 2],[1 2])

　　

 

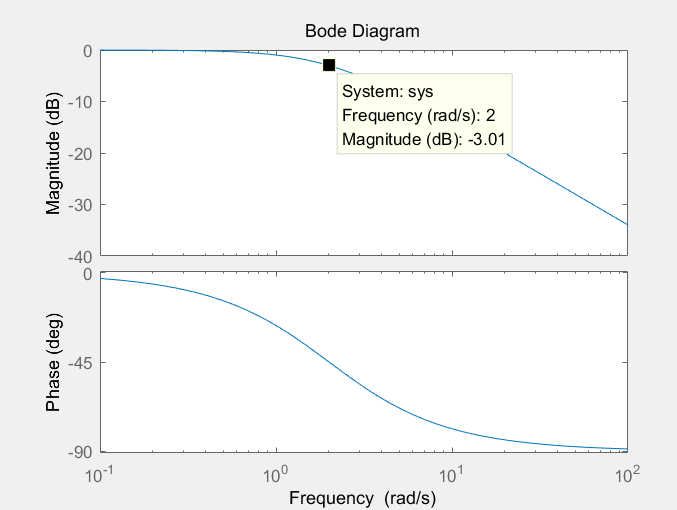
 　　G(s)= s + 1时，伯德图如下：

　　可以看出，

　　

　　

 

　　

 

 　　

 

 　　

 

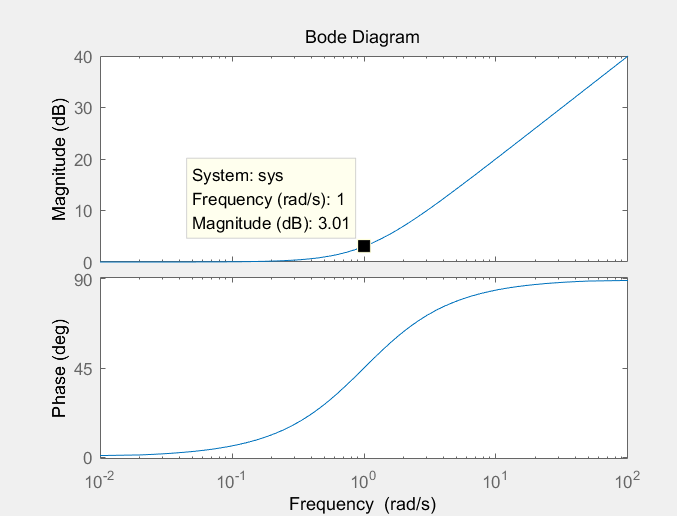
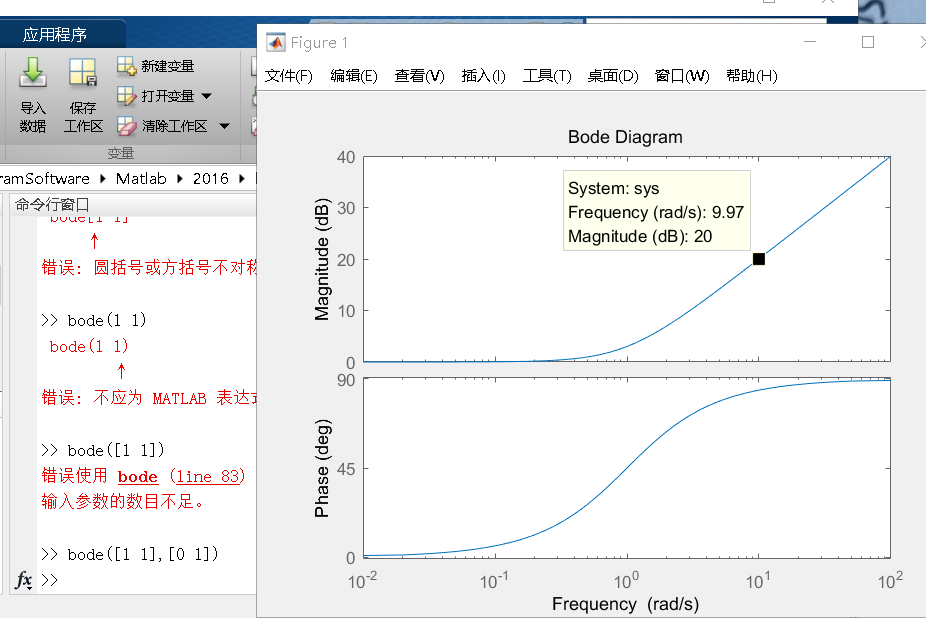
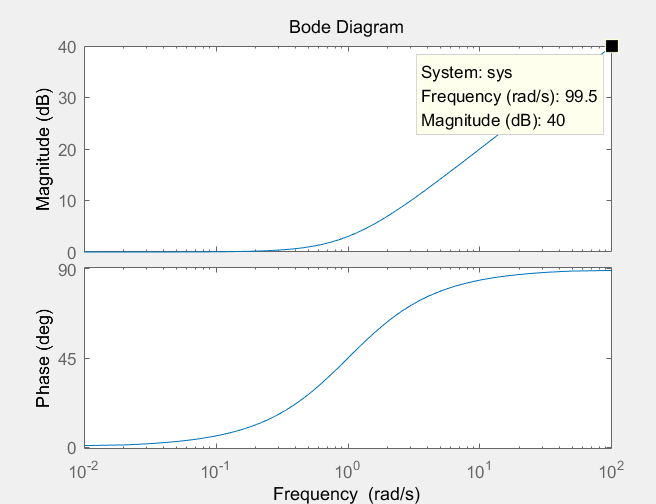
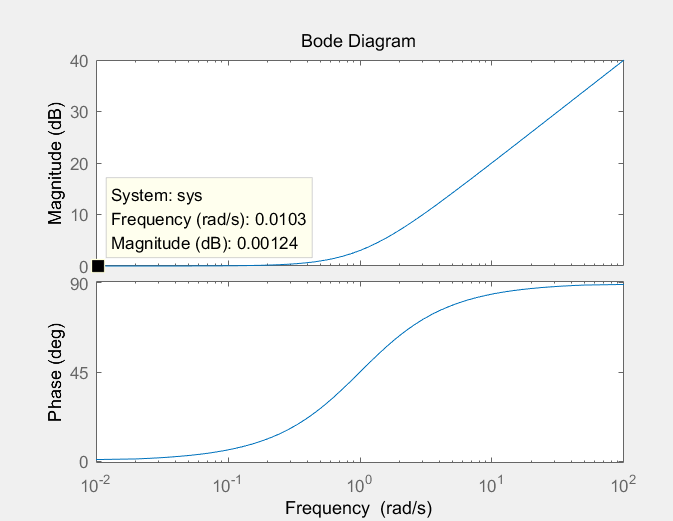
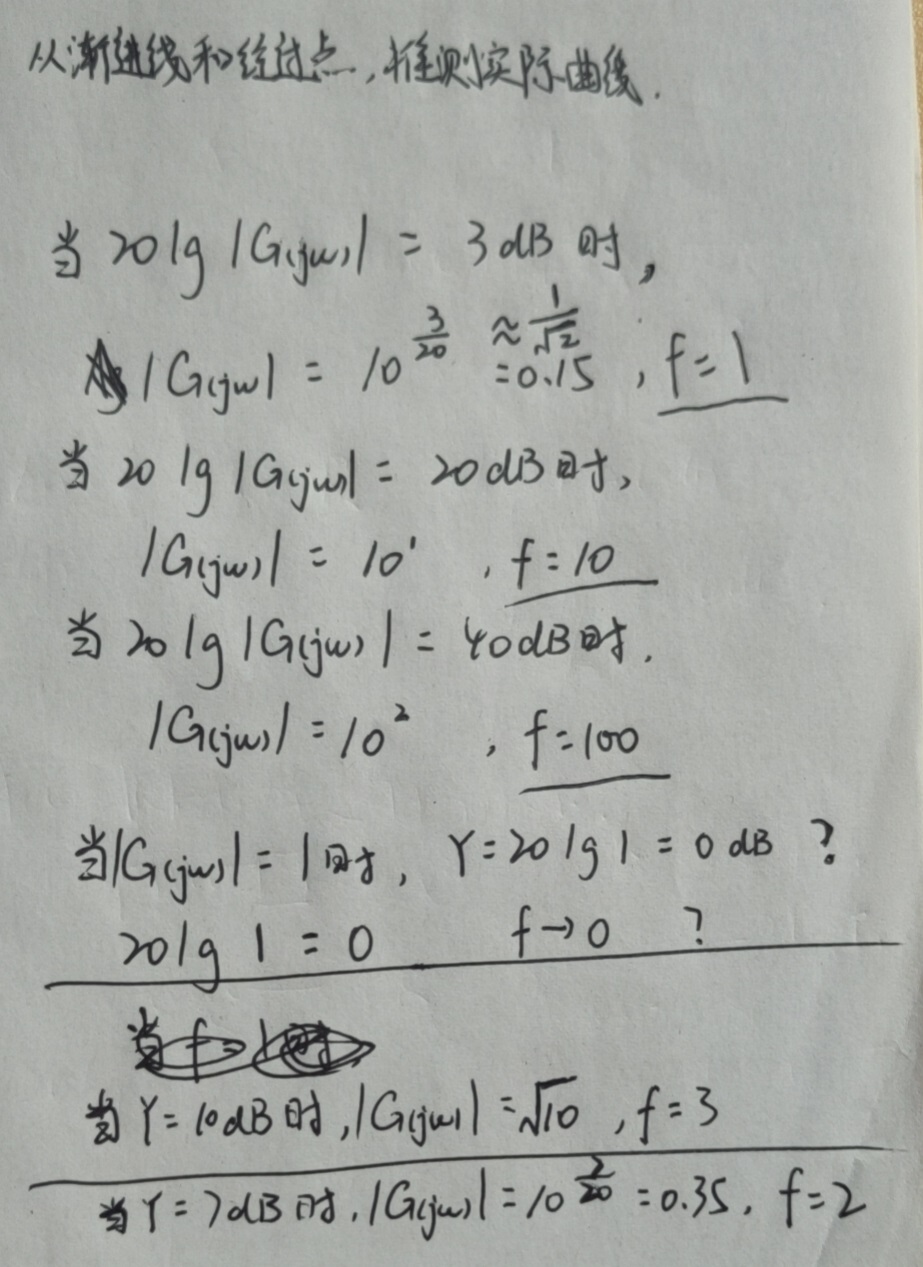
　　可以看到当频率w在截止频率附近时，变化非常大，从小于截止频率时的接近于0，

　　再到根号2分之1，直到十倍、百倍。

 

16.  伯德图手绘技巧与应用

 　　

 

自动控制原理学习内容预览：