FPGA实现图像的非线性变换：伽玛（幂律）变换
伽玛变换又名指数变换、幂次变换或幂律变换，是另一种常用的非线性变换。
一、伽玛（幂律）变换理论
伽玛变换的一般表达式为：s = c·rγ
其中 c 和 γ 为正常数，有时考虑到偏移量，也将表达式写为 s=c(r+ ε)γ。与对数变换不同，伽玛变换可以根据 y 的不同取值选择性地增强低灰度区域的对比度或是高灰度区域的对比度。y是图像灰度校正中非常重要的-一个参数，其取值决定了输入图像和输出图像之间的灰度映射方式，即决定了是增强低灰度( 阴影区域)还是增强高灰度(高亮区域)。其中：
● y>1时，图像的高灰度区城对比度得到增强；
● y<1时，图像的低灰度区域对比度得到增强；
● y=1时，这一灰度变换是线性的，即不改变原图像。
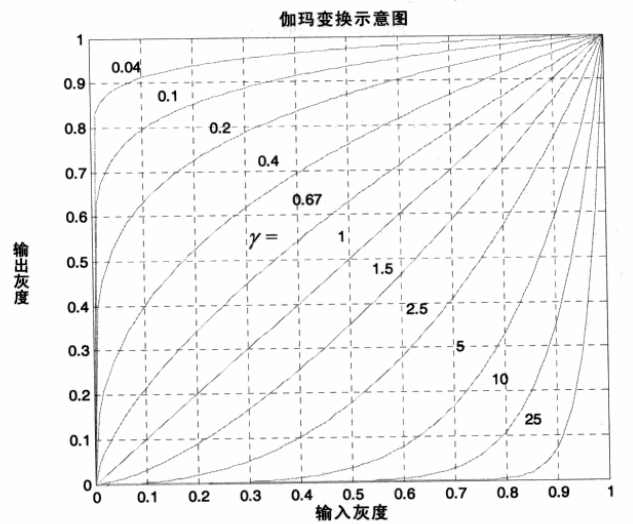
伽玛变换的映射关系如图所示。在进行变换时，通常需要将0~255的灰度动态范围首先变换到 0~1 的动态范围，然后执行伽玛变换后再回复原动态范围。
灰度图彩色图都可以进行伽玛变换，下面的案例直接拿彩色图案来测试结果。
二、MATLAB实现
%-------------------------------------------------------------------------- %-- gamma变换 %-------------------------------------------------------------------------- clear all close all clc I = imread('img.jpg'); %读入原图像 subplot(3,1,1);imshow(imadjust(I,[],[],0.75));title('Gamma 0.75'); subplot(3,1,2);imshow(imadjust(I,[],[],1 ));title('Gamma 1'); subplot(3,1,3);imshow(imadjust(I,[],[],1.5 ));title('Gamma 1.5');
由 MATLAB 可以看出的确符合上面说的结论：
● y>1时，图像的高灰度区城对比度得到增强，图像看起来变暗了；
● y<1时，图像的低灰度区域对比度得到增强，图像看起来变亮了；
● y=1时，这一灰度变换是线性的，即不改变原图像。
三、FPGA实现
1、log函数查找表
对于 FPGA 来说，直接实现对数公式难度很大，像这种问题我们多采用基于查找表的方式进行对数变换。ROM 表的制作可以用MATLAB实现，代码如下所示：
%-------------------------------------------------------------------------- %-- 生成gamma校正所需的rom mif文件 %-------------------------------------------------------------------------- clear all close all clc depth = 256; width = 8; r = [0:1:255]; %-------------------------------------------------------------------------- %-- sqrt开根 %-------------------------------------------------------------------------- s_qrt = 16*sqrt(r); %开根 z1 = round(s_qrt); fid = fopen('sqrt.mif','w'); fprintf(fid,'depth= %d; \n',depth); fprintf(fid,'width= %d; \n',width); fprintf(fid,'address_radix=uns;\n'); fprintf(fid,'data_radix = uns;\n'); fprintf(fid,'Content Begin \n'); for(k=1:depth) fprintf(fid,'%d: %d; \n',k-1,z1(k)); end fprintf(fid,'end;'); %-------------------------------------------------------------------------- %-- square开方 %-------------------------------------------------------------------------- s_quare = (1/256)*r.^2; %平方 z2 = round(s_quare); fid = fopen('square.mif','w'); fprintf(fid,'depth= %d; \n',depth); fprintf(fid,'width= %d; \n',width); fprintf(fid,'address_radix=uns;\n'); fprintf(fid,'data_radix = uns;\n'); fprintf(fid,'Content Begin \n'); for(k=1:depth) fprintf(fid,'%d: %d; \n',k-1,z2(k)); end fprintf(fid,'end;'); %-------------------------------------------------------------------------- %-- 曲线展示 %-------------------------------------------------------------------------- hold on plot(r); %原曲线 plot(s_qrt); %开根 plot(s_quare); %开方 legend('原曲线','开根曲线','开方曲线'); hold off
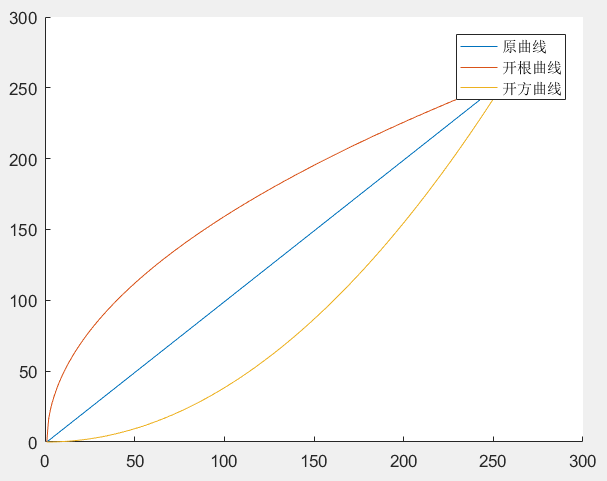
点击运行就可以得到 sqrt.mif 和 square.mif 文件，分别代表了 γ ＜ 1 和 γ ＞ 1 的情况。此外可以看到这次采用的 γ 曲线如图所示：
2、代码设计
有了 rom 查找表，代码设计变得异常简单，直接拿数据进查找表对照即可，和上篇博客是一样的操作，关键代码如下所示：
//========================================================================== //== RGB565转RGB888 //========================================================================== assign R = {RGB_data[15:11],RGB_data[13:11]}; assign G = {RGB_data[10: 5],RGB_data[ 6: 5]}; assign B = {RGB_data[ 4: 0],RGB_data[ 2: 0]}; //========================================================================== //== gamma sqrt 图像变亮 //========================================================================== rom_sqrt u_R_sqrt ( .address (R ), .clock (clk ), .q (R_sqrt ) ); rom_sqrt u_G_sqrt ( .address (G ), .clock (clk ), .q (G_sqrt ) ); rom_sqrt u_B_sqrt ( .address (B ), .clock (clk ), .q (B_sqrt ) ); assign gamma_data_sqrt = {R_sqrt[7:3],G_sqrt[7:2],B_sqrt[7:3]}; //========================================================================== //== gamma square 图像变暗 //========================================================================== rom_square u_R_square ( .address (R ), .clock (clk ), .q (R_square ) ); rom_square u_G_square ( .address (G ), .clock (clk ), .q (G_square ) ); rom_square u_B_square ( .address (B ), .clock (clk ), .q (B_square ) ); assign gamma_data_square = {R_square[7:3],G_square[7:2],B_square[7:3]}; //========================================================================== //== 信号同步，rom给地址到出数据会延迟1clk //========================================================================== always @(posedge clk or negedge rst_n) begin if(!rst_n) begin RGB_de_r <= 1'b0; RGB_hsync_r <= 1'b0; RGB_vsync_r <= 1'b0; end else begin RGB_de_r <= RGB_de; RGB_hsync_r <= RGB_hsync; RGB_vsync_r <= RGB_vsync; end end assign gamma_de = RGB_de_r; assign gamma_hsync = RGB_hsync_r; assign gamma_vsync = RGB_vsync_r;
四、上板验证
sqrt开根的伽马图：
原图：
square 开方的伽马图：
虽然我的板子坏了，但总的效果还是成功的，图像在不同的 γ 值下效果不同，sqrt开根操作（γ＜1）时整体变亮，square开方操作（γ＞1）是整体变暗，和MATLAB的效果差不多，实验成功。
参考资料：
[1] OpenS Lee：FPGA开源工作室（公众号）
[2] 张铮, 王艳平, 薛桂香. 数字图像处理与机器视觉[M]. 人民邮电出版社, 2010.
