数据和算法【树和二叉树】
树的机构与线性结构的区别
1)一个结构如果不空,其中就存在着唯一的起始结点,称为根(root)
2)按结构的连接关系,树根外的其余结点都有且只有一个前驱,但是一个结点可以有0个或者多个后继。在非空的树结构中一定有些结点并不连接到其他结点。这种结点与表的尾结点性质类似,但在一个数结构里可以存在多个这种结点。
3)结构里的所有结点都在树根结点通过后继关系可达的结点集合里。(从树根出发,经过若干次后继关系可以到达结构中的任一个结点)
4)结点之间的联系不会形成循环关系,结点之间的联系形成了一个序,但一般而言不像线性表那样形成一个全序。
5)从这种结构里的任意两个不同结点出发,通过后继关系可达的两个结点集合,或者互不相交,或者一个集合是另一个集合的子集。
二叉树:概念和性质
二叉树是一种最简单的树形结构,其特点是树中每个结点至多关联到两个后继结点,也就是说,一个结点的关联结点数可以为0、1或2。另一特点是一个结点关联的后继结点明确地分左右,或为其左关联结点,或为其右关联结点。
定义:
二叉树是结点的有穷集合。这个集合或者是空集,或者其中有一个称为根节点的特殊结点,其余结点分属两棵不相交的二叉树,这两棵二叉树分别是原二叉树(或说是原二叉树的根节点)的左子树和右子树。
不包含任何结点的二叉树称为空树;只包含一个结点的二叉树是一颗单点树;一颗二叉树可以包含任意(但有穷多)个结点。
一颗二叉树的根节点称为该树的子树根节点的父节点;子树的根节点称为二叉树树根结点的子节点。
在二叉树里有些结点的两棵子树都为空,没有子节点,这种结点称为树叶。
一个结点的子结点个数称为该结点的度数。
性质1:在非空二叉树第 i 层中至多有2**i个结点(i>=0)
性质2:高度为h的二叉树至多有2**(h+1) - 1个结点
性质3:对于任何非空二叉树T,如果其叶结点的个数n0,度数为2的结点个数为n2,那么n0 = n2 + 1
满二叉树:如果二叉树中所有分支结点的度数都是2,则称它为一颗满二叉树。满二叉树是一般二叉树的一个子集。
性质4:满二叉树里的叶结点比分支结点多一个。
扩充二叉树:对二叉树T,加入足够多的新叶结点,使T的原有结点都变成度数为2的分支结点,得到的二叉树称为T的扩充二叉树。扩充二叉树中新增的结点称为其外部结点,原树T的结点称为其内部结点,空树的扩充二叉树规定为空树。
完全二叉树:对于一颗高度为h的二叉树,如果其第0层至第h-1层的结点都满。如果最下一层的结点不满,则所有结点在最左边连续排列,空位都在右边。这样的二叉树就是一颗完全二叉树。
性质6:n个结点的完全二叉树高度h=lgn,即为不大于lgn的最大整数。
树的遍历:深度优先遍历和宽度优先遍历
深度优先遍历:
遍历左子树、遍历右子树和访问根结点
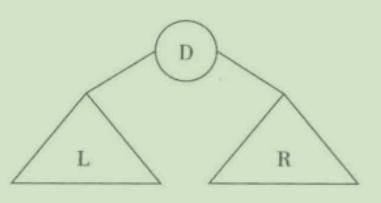
三种常见的遍历顺序:
先根序遍历(DLR)
中根序遍历(LDR,也叫对称)
后根序遍历(LRD)
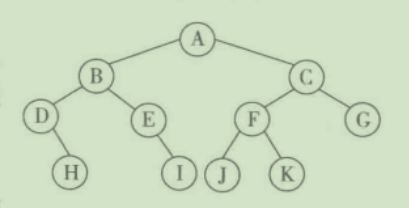
按先根序遍历,得到结点访问顺序:ABDHEICFJKG
按对称遍历,得到结点访问顺序:DHBEIAJFKCG
按后根序遍历,得到结点访问顺序:HDIEBJKFGCA
宽度优先遍历:
宽度优先是按路径长度由近到远地访问结点。上图按照宽度优先遍历的顺序:ABCDEFGHIJK
二叉树的list实现
def BinTree(data, left=None, right=None): return [data, left, right] def is_empty_BinTree(btree): return btree is None def root(btree): return btree[0] def left(btree): return btree[1] def right(btree): return btree[2] def set_root(btree, data): btree[0] = data def set_left(btree, left): btree[1] = left def set_right(btree, right): btree[2] = right
二元表达式和二叉树
数学表达式具有分层次的递归结构,一个运算符作用与相应对象,其运算对象又可以是任意复杂的表达式。二叉树的递归结构正好用来表示这种表达式:二叉树中结点与子树的关系可用于表示运算符对运算对象的作用关系。
二元表达式可以很自然地映射到二叉树:
1)以基本运算对象作为叶结点中的数据。
2)以运算符作为分支结点的数据:其两棵子树是它的运算对象;子树可以是基本运算对象,也可以是任意复杂的二元表达式。
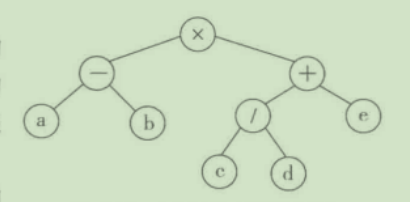
先根序遍历得到:*-ab+/cde,正是该表达式的前缀表示。
后根序遍历得到:ab-cd/e+*,正是该表达式的后缀表示形式。
对称遍历得到:a-b*c/d+e,正是该表达式的中缀表示形式。


