数据和算法【线性表】
表的概念和性质
在抽象地讨论线性表时,首先要考虑一个(有穷的或无穷的)基本元素集合E,集合E中的元素可能都是某个类型的数据对象。
在一个非空的线性表里,存在着唯一的一个首元素和唯一的尾元素。除首元素之外,表中的每个元素e都有且仅有一个前驱元素;除了尾元素之外的每个元素都有且仅有一个后继元素。
线性表的实现
将表中元素顺序存放在一大块连续的存储区里,这样实现的表也称为顺序表(或连续表)。在这种实现中,元素间的顺序关系由它们的存储顺序自然表示。
将表元素存放在通过链接构造起来的一系列存储块里,这样实现的表称为链接表,简称链表。
顺序表的实现
如果表里的元素大小相同,假定表元素编号从0开始,元素e0自然应存储在内存位置Loc(e0) = l0,再假定表中一个元素所需的存储单元数为c=size(元素),在这种情况下,就有下面的简单元素ei的地址计算公式:
Loc(ei) = Loc(e0) + c * i
如果表元素大小不统一,按照上面的方案将元素顺序存入元素存储区,将无法通过统一公式计算元素位置。这时可以采用另一种布局方案。将实际数据元素另行存储,在顺序表里各单元位置保存对应元素的引用信息(地址),由于每个地址所需的存储量相同,可以计算出元素地址的存储位置,而后地址做一次间接访问,就能得到实际元素的数据了。

顺序表的基本操作的实现
创建空表
简单判断操作
访问给定下标i的元素
遍历操作
查找给定元素d的(第一次出现的)位置
查找给定元素d在位置 k之后的第一次出现的位置
变动操作:加入元素:
尾端加入新数据项:O(1)
新数据存入元素存储区的第i个单元:要求无序:O(1),要求保序:O(n)
变动操作:删除元素:
尾端删除元素:O(1)
删除位置i的数据:要求无序:O(1),要求保序:O(n)
基于条件的删除:O(n)
表的顺序实现(顺序表)的总结:
优点:O(1)时间的(随机、直接的)按位置访问元素;元素在表里存储紧凑,除表元素存储区之外只需要O(1)空间存放少量辅助信息。
缺点:需要连续的存储区存放表中的元素,如果表很大,就需要很大片的连续内在空间。一旦确定了存储块的大小,可容纳单元个数并不随着插入/删除操作的进行而变化。如果很大的存储区里只保存了少量数据项,就会有大量空闲单元,造成表内的存储浪费。另外,在执行加入或删除操作时,通常需要移动许多元素,效率低。最后,建立表时需要考虑元素存储区大小,而实际需求通常很难事先估计。
顺序表的结构
两种基本的实现方式:一体式结构 / 分离式结构

采用一体式结构,如果不断地向元素存储区添加元素,最终一定会填满其元素存储区。一体式结构不能扩大其存储。要想继续工作,就只能另外创建一个容量更大地对象,把元素搬过去。但是这是一个新对象。
采用分离式结构就简单得多,可以在不改变对象的情况下换一块更大的元素存储区,使加入元素操作可以正常完成。操作过程:
1)另外申请一块更大的元素存储区
2)把表中已有的元素复制到新存储区
3)用新的元素存储区替换原来的元素存储区(改变表对象中的元素链接)
4)实际加入新元素。
这种技术实现的顺序表称为动态顺序表
python中的list:
python标准类型list就是一种元素个数可变的线性表,可以加入和删除元素,在各种操作中维持已有元素的顺序。其重要的实现约束还有:
1)基于下标(位置)的高效元素访问和更新,时间复杂度应该是O(1)
2)允许任意加入元素(不会出现由于表满而无法加入新元素的情况),而且在不断加入元素的过程中,表对象的标识(函数id得到的值)不变。
list需要维持元素的顺序,这种表只能采用连续表技术,表中元素保存在一块连续的存储区里;能容纳任意多的元素,就必须能更换元素存储区。要想在更换存储区时list对象的标识(id)不变,只能采用分离实现技术。
python中list采用如下实际策略:在建立空表时,系统分配一块能容纳8个元素的存储区;在执行插入操作(insert或append)时,如果元素区满就换一块4倍大的存储区。但如果当时的表已经很大,系统将改变策略,换存储区时容量加倍,这里的“很大”是一个实际确定的参数,目前的值是50000。引入后一个策略是为了避免出现过多空闲的存储位置。
顺序表的简单总结
采用顺序表结构实现线性表:
1)最重要的特点(优势)是O(1)时间的定位元素访问。很多简单操作的效率也比较高。
2)这里最重要的麻烦是加入/删除等操作的效率问题。这类操作改变表中元素序列的结构,是典型的变动操作。由于元素在顺序表的存储区里连续排列,加入/删除操作有可能要移动很多元素,操作代价高。
3)只有特殊的尾端插入/删除操作具有O(1)时间复杂度。但插入操作复杂度还受到元素存储区固定大小的限制。通过适当的(加倍)存储区扩充策略,一系列尾端插入可以达到O(1)的平均复杂度。
顺序表的优点和缺点都在于其元素存储的集中方式和连续性。从缺点看,这样的表结构不够灵活,不容易调整和变化。如果在一个表的使用中需要经常修改结构,用顺序表去实现就不太方便,反复操作的代价可能很高。
还有一点问题 也值得提出:如果程序里需要巨大的线性表,采用顺序表实现就需要巨大块的连续存储空间,这也可能造成存储管理方面的困难。
链接表
实现线性表的基本需求是:
1)能够找到表中的首元素
2)从表里的任一元素出发,可以找到它之后的下一个元素
用链接关系显示表示元素之间的顺序关联。基于链接技术实现的线性表称为链接表或者链表。采用链接方式实现线性表的基本思路 :
1)把表中的元素分别放存储在一批独立的存储块(称为表的结点)里。
2)保证从组成表结构中的任一个结点可找到与其相关的下一个结点。
3)在前一结点里用链接的方式显示地记录下与下一结点之间的关联。
单向链表
一个单链表由一些具体的表结点构成。每个结点是一个对象,有自己的标识,下面也常称其为该结点的链接。结点之间通过结点链接建立起单向的顺序联系。
基本链表操作
创建空链表:只需要把相应的表头变量设置为空链接
删除链表:应丢弃这个链表里的所有结点。这个操作的实现与具体的语言环境有关。在python中只需要将表指针赋值为None,就抛弃了链表原有的所有结点。
判断链表是否为空:将表头变量的值与空链接比较。
判断表是否满:一般而言链表不会满,除非程序用完了所有可用的存储空间。
加入元素:
表首端插入:首端插入元素要求把新数据元素插入表中,作为表的第一元素,这是最简单的情况。这一操作需要通过三步完成:
1)创建一个新结点并存入数据。
2)把原链表首结点的链接存入新结点的链接域next,这一操作将原表的一串结点链接在刚创建的新结点之后。
3)修改表头变量,使之指向新结点,这个操作使新结点实际成为表头变量所指的结点,即表的首结点。
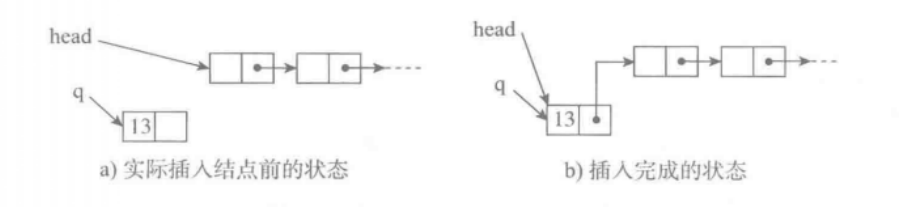
一般情况的元素插入:要想在单链表里的某位置插入一个新结点。必须先找到该位置之前的那个结点,因为新结点需要插入在它的后面,需要修改它的next域。设变量pre已指向要插入元素位置的前一结点,操作也分三步:
1)创建一个新结点并存入数据
2)把pre所指结点next域的值存入新结点的链接域next,这个操作将原表在pre所指结点之后的一段链接到新结点之后。
3)修改pre的next域,使之指向新结点,这个操作把新结点链入被操作的表。

删除元素:删除链表中元素,也可以通过调整表结构删除表中结点的方式完成:
删除表首元素:删除表中第一个元素对应于删除表的第一个结点,为此只需要修改表头指针,令其指向表中第二个结点。丢弃不用的结点将被python解释器自动回收:head = head.next
一般情况的元素删除:一般情况删除须先找到要删元素所在结点的前一结点,设用变量pre指向,然后修改pre的next域,使之指向被删除结点的下一结点:pre.next = pre.next.next
扫描、定位和遍历:
按下标定位:链表首结点的元素应看作下标0,其他元素一次排列。确定第i个元素所在结点的操作称为按下标定位,可以参考表扫描模式写出:
p = head while p is not None and i > 0: i -= 1 p = p.next
假设循环前变量i已有所需的值,循环结束时可能出现两种情况:或者扫描完表中所有结点还没有找到第i个结点,或者p所指结点就是所需。通过检查p值是否为None可以区分这两中情况。显然,如果现在需要删除第k个结点,可以先将i设置为k-1,循环后检查i是0且p.next不是None就可以执行删除了。
按元素定位:假设需要在链表里找到满足谓词pred的元素。同样可以参考上面的表扫描模式:
p = head while p is not None and not pred(p.elem): p = p.next
链表操作的复杂度
创建空表:O(1)
删除表:在python里是:O(1)
判断空表:O(1)
加入元素:
首端加入元素:O(1)
尾端加入元素:O(n)
定位加入元素:O(n)
删除元素:
首端删除元素:O(1)
尾端删除元素:O(n)
定位删除元素:O(n)
其他删除:通常需要扫描整个表或其一部分,O(n)
单链表类的定义,初始化函数和简单操作
class LList: def __init__(self): self._head = None def is_empty(self): return self._head is None def prepend(self, elem): self._head = LNode(elem, self._head) def pop(self): if self._head is None: raise LinkedListUnderflow("in pop") e = self._head.elem self._head = self._head.next return e def append(self, elem): if self._head is None: self._head = LNode(elem) return p = self._head while p.next is not None: p = p.next p.next = LNode(elem) def pop_last(self): if self._head is None: raise LinkedListUnderflow("in pop_last") p = self._head if p.next is None: e = p.elem self._head = None return e while p.next.next is not None: p = p.next e = p.next.elem p.next = None return e def find(self, pred): p = self._head while p is not None: if pred(p.elem): return p.elem p = p.next def printall(self): p = self._head while p is not None: print(p.elem, end="") if p.next is not None: print(", ", end="") p = p.next print("") def elements(self): p = self._head while p is not None: yield p.elem p = p.next def filter(self, pred): p = self._head while p is not None: if pred(p.elem): yield p.elem p = p.next
链表的变形和操作
前面单链表实现有一个缺点:尾端加入元素操作的效率低,因为这时只能从表头开始查找,直至找到表的最后一个结点,而后才能链接新结点。
优化:给表对象增加一个表尾结点引用域,只需要常量时间就能找到尾结点,在尾结点加入新结点的操作就可能做到O(1)。
class LList1(LList): def __init__(self): super().__init__() self._rear = None def prepend(self, elem): if self._head is None: self._head = LNode(elem, self._head) self._rear = self._head else: self._head = LNode(elem, self._head) def append(self, elem): if self._head is None: self._head = LNode(elem, self._head) self._rear = self._head else:
# 将新加入的结点连在现有尾端结点后 self._rear.next = LNode(elem)
# 将尾端结点指向新加入的加点 self._rear = self._rear.next def pop_last(self): if self._head is None: raise LinkedListUnderflow("in pop_last") p = self._head if p.next is None: e = p.elem self._head = None return e while p.next.next is not None: p = p.next e = p.next.next p.next = None self._rear = p return e
循环单链表
单链表的另一常见变形是循环单链表(简称循环链表),其中最后一个结点的next域不用None,而是指向表的第一个结点,但仔细考虑,就会发现在链表对象里记录表尾结点更合适,这样就可以同时支持O(1)时间的表头/表尾插入和O(1)时间的表头删除。当然,由于循环链表里的结点连成一个圈,哪个结点算是表头或表尾,只要是概念问题,从表的内部形态上无法区分。

class LCList: def __init__(self): self._head = None def is_empty(self): return self._head is None def prepend(self, elem): p = LNode(elem) if self._rear is None: p.next = p self._rear = p else: p.next = self._rear.next self._rear.next = p def append(self, elem): self.prepend(elem) self._rear = self._rear.next def pop(self): if self._rear is None: raise LinkedListUnderflow("in pop of CLList") p = self._rear.next if self._rear is p: self._rear = None else: self._rear.next = p.next return p.elem
双链表
单链表只有一个方向的链接,只能做一个方向的扫描和逐步操作。即使增加了尾结点引用,也只能支持O(1)时间的首端加入/删除和尾端加入。如果希望两端插入和删除操作都能高效完成,就必须修改结点的基本设计,加入另一种方向的链接,这样就得到了双向链接表,简称双链表。
双链表类
class LNode: def __init__(self, elem, next_=None): self.elem = elem self.next = next_
class DLNode(LNode): def __init__(self, elem, prev=None, next_=None): super().__init__(elem, next_) self.prev = prev
class DLList(LList1): def __init__(self): super().__init__() def prepend(self, elem): p = DLNode(elem, None, self._head) if self._head is None: self._rear = p else: p.next.prev = p self._head = p def append(self, elem): p = DLNode(elem, self._rear, None) if self._head is None: self._head = p else: p.prev.next = p self._rear = p def pop(self): if self._head is None: raise LinkedListUnderflow("in pop of DLList") e = self._head.elem self._head = self._head.next if self._head is not None: self._head.prev = None return e def pop_last(self): if self._head is None: raise LinkedListUnderflow("in pop_last of DLList") e = self._rear.elem self._rear = self._rear.prev if self._rear is None: self._head = None else: self._rear.next = None return e
两个链表操作
链表反转
链表反转有两种方式,第一种是结点之间搬动元素,但是时间复杂度是O(n**2);第二种是修改结点的链接关系,通过改变结点的链接顺序来改变表元素的顺序。
下面是LList类的反转方法,在LList1中还需要考虑_rear:
def rev(self): p = None while self._head is not None: q = self._head # self._head = q.next self._head = self._head.next q.next = p p = q self._head = p
链表排序
第一种:结点之间搬动元素,插入排序:
def sort(self): if self._head is None: return crt = self._head.next while crt is not None: x = crt.elem p = self._head while p is not crt and p.elem <= x: p = p.next while p is not crt: y = p.elem p.elem = x x = y p = p.next crt.elem = x crt = crt.next
第二种:种是修改结点的链接关系,插入排序:
def sort(self): p = self._head if p is None or p.next is None: return rem = p.next p.next = None while rem is not None: p = self._head prev = None while p is not None and p.elem <= rem.elem: prev = p p = p.next if prev is None: self._head = rem else: prev.next = rem prev = rem rem = rem.next prev.next = p
不同链表的简单总结
1)基本单链表包含了一系列结点,通过y一个方向的链接构造起来。它支持高效的前端插入和删除操作,定位操作或尾端操作都需要O(n)时间。
2)增加了尾结点引用域的单链表可以很好地支持首端/尾端插入和首端弹出元素,它们都是O(1)时间复杂度的操作,但不能支持高效的尾端删除。
3)循环单链表也能支持高效的表首端/尾端插入和首端弹出元素。需要特别注意结束判断问题。
4)双链表中每个结点都有两个方向的链接,因此可以高效地找到前后结点。如果有尾端点引用,两端插入和删除都能在O(1)时间完成。循环双链表类似。
5)对于单链表,遍历和数据检索操作都只能从表头开始,需要O(n)时间。对于双链表,这些操作可以从表头或表尾开始,复杂度不变。与它们对应的两种循环链表,遍历和检索可以从表中任何一个地方开始,但要注意结束条件。
链表的一些重要的优点:
1)表结构是通过一些链接起来的结点形成的,结点之间的顺序由链接关系决定,链接可以修改,因此表的结构很容易调整和修改。
2)不需要修改结点里的数据元素或移动它们,只通过修改结点之间的链接,就能灵活地修改表的结构和数据排列方式。
3)整个表由一些小的存储块构成,比较容易安排和管理。用python编写程序时,这些问题由解释器负责,程序员不必处理,但了解情况也很重要。
链表的一些明显的缺点:
1)定位访问需要线性时间,这是与顺序表相比的最大劣势。
2)简单单链表上的尾端操作需要线性时间。增加一个尾指针,可以将尾端插入变成常量时间操作,但仍不能有效实现尾端删除。双链表通过在每个结点里增加第二个链接,可以实现两端的高效插入和删除。
3)要找当前元素的前一元素,必须从头开始扫描表结点。这种操作应尽量避免。双链表可以解决这个问题,但每个结点要付出更多存储代价。
4)为存储一个表元素,需要多用一个链接域,这是实现链接表的存储代价。双链表可以提高链表操作的灵活性,但需要增加两个链接域。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号