Mathematics for Computer Science1--Proofs

Simply put, a proof is a method of establishing truth.

Like beauty, “truth” sometimes depends on the eye of the beholder, and it should not be surprising that what

constitutes a proof differs among fields. For example, in the judicial system, legal truth is decided by a jury based on the allowable evidence presented at trial. In the business world, authoritative truth is specifified by a trusted person or organization,or maybe just your boss. In fifields such as physics and biology, scientifific truth1 is

confifirmed by experiment. In statistics, probable truth is established by statistical analysis of sample data.

Philosophical proof involves careful exposition and persuasion typically based on a series of small, plausible arguments. The best example begins with “Cogitoergo sum,” a Latin sentence that translates as “I think, therefore I am.” It comes from the beginning of a 17th century essay by the mathematician/philosopher,

Ren´eDescartes, and it is one of the most famous quotes in the world: do a web search on the phrase and you will be flflooded with hits.

Deducing your existence from the fact that you’re thinking about your existenceis a pretty cool and persuasive-sounding idea. However, with just a few more lines of argument in this vein, Descartes goes on to conclude that there is an infifinitely benefificent God. Whether or not you believe in a benefificent God, you’ll probably agree that any very short proof of God’s existence is bound to be far-fetched.

So even in masterful hands, this approach is not reliable.

 

Mathematics has its own specifific notion of “proof.”

Defifinition. A mathematical proof of a proposition is a chain of logical deductions

leading to the proposition from a base set of axioms.

The three key ideas in this defifinition are highlighted: proposition, logical deduction, and axiom. These three ideas are explained in the following chapters,beginning with propositions in Chapter 1. We will then provide lots of examples of proofs and even some examples of “false proofs” (that is, arguments that look like a proof but that contain missteps, or deductions that aren’t so logical when examined closely). False proofs are often even more important as examples than correct proofs, because they are uniquely helpful with honing your skills at making sure each step of a proof follows logically from prior steps.

 

Propositions

Defifinition. A proposition is a statement that is either true or false.

eg,

Proposition 1.0.1.    2 + 3 = 5.

Proposition 1.0.2.   1 + 1 = 3.

Compound Propositions

In general, a truth table indicates the true/false value of a proposition for each possible setting of the variables. 

We can precisely defifine these special words using truth tables.

NOT, AND, and OR

If P and Q denotes an arbitrary proposition, then the truth of the propositions is defifined by the following truth table:

 

 

 

 

 

 

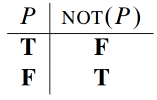
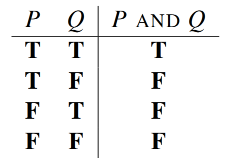
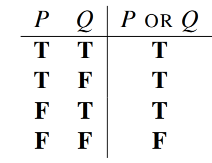
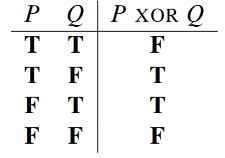
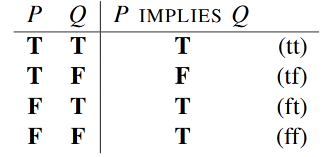
An implication is true exactly when the if-part is false or the then-part is true.

p->q,说明p是q的子集

 

 

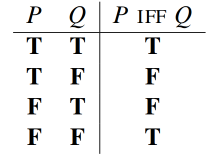
The proposition “P if and only if Q” asserts that P and Q are logically equivalent; that is, either both are true or both are false.

Notation

 

 

Predicates and Quantififiers

 

A predicate is a proposition whose truth depends on the value of one or more variables.a function-like notation is used to denote a predicate supplied with specifific variable

values. For example, we might name our earlier predicate P:

P (n) :: = “n is a perfect square”

 

There are a couple of assertions commonly made about a predicate: that it is some

times true and that it is always true.