线性代数及其应用（二）

向量方程

线性方程组的重要性质都可用向量概念与符号来描述。

R²中的向量:

　　仅含一列的矩阵称为列向量，或简称向量，包含两个元素的向量如下：

　　

 

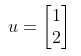
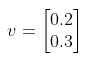
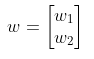
 　  其中w₁和w₂是任意实数，所有两个元素的向量集记为R²，R表示向量中的元素是实数，而指数2表示每个向量包含两个元素. 

　　给定R²中两个向量u和v，它们的和u+v是把u和v对应元素相加所得的向量，如

　　

 

 　　

\begin{bmatrix}
1\\ 
-2\\
\end{bmatrix}
+
\begin{bmatrix}
2\\ 
5\\
\end{bmatrix}
=
\begin{bmatrix}
1+2\\ 
-2+5\\
\end{bmatrix}
=
\begin{bmatrix}
3\\ 
3\\
\end{bmatrix}

 

　　给定向量u和实数c,u与c的标量乘法（或数乘）是把u的每个元素乘以c,所得向量记为cu，例如：

　　若 , c = 5,则

 

       

 

 

cu = 5\begin{bmatrix}
3\\ 
-1\\
\end{bmatrix}
=
\begin{bmatrix}
15\\ 
-5\\
\end{bmatrix}

 

 R²的几何表示

　　考虑平面上的直角坐标系，因为平面上每个点由实数的有序对确定，所以可把几何点(a,b) 与列向量等同，因此我们可把R²看作平面上所有点的集合

 

　　

 　　  

 

 

 

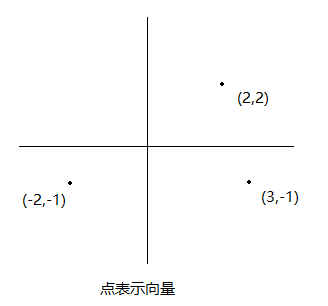
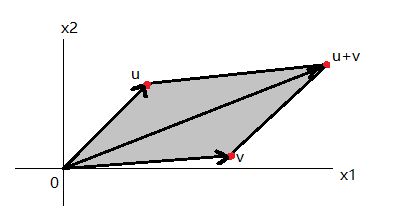
 　　两个向量的和的几何意义

　　

 

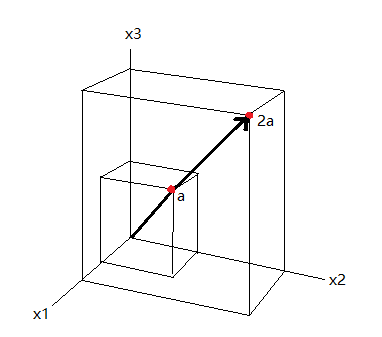
　　R³中的向量

　　

 

 

　　Rⁿ中的代数性质 （对Rⁿ中一切向量u,v,w以及标量c和d）：

　　1. u + v = v + u

　　2.(u+v)+w = u+(v+w)

　　3.(u+0)=0+u=u

　　4.u+(-u) = -u+u =0

　　5.c(u+v)=cu+cv

　　6.(c+d)u=cu+du

　　7.c(du)=(cd)u

　　8.1u=u

 

　　线性代数的一个主要思想是研究可以表示为某一个固定向量集合{v₁,v₂,....v_p}的线性组合的所有向量

　　Span{v} 与 Span{u,v}的几何解释

　　设v是R³中的向量，那么Span{v}就是v的所有标量倍数的集合，也就是R³中通过v和0的直线上所有点的集合

　　

 　　

 

 

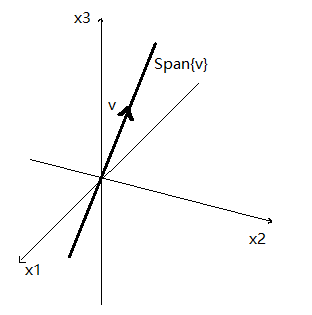
　　　若u和v是R³中的非零向量，v不是u的倍数，则Span{u,v}是R³中包含u,v和0的平面，特别地，Span{u,v}包含R³中通过u与0的直线，也包含通过v与0的直线，反正就是确定了一个平面。

　　　　

 　　

 

 

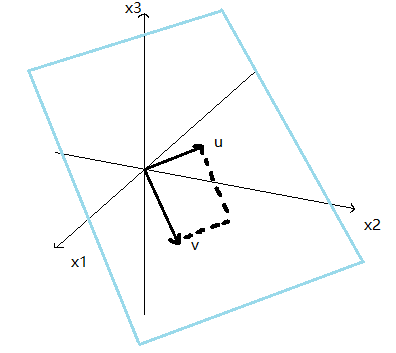
 　　蓝色范围在概念上无限扩充。