Eigen : The Matrix Class

Eigen库 矩阵类的使用：

（本文根据官方文档加上自己的一些理解修改制成）

 

首先关于Matrix的定义：  Matrix<typename scalar, int RowsAtCompileTime, int ColsAtCompileTime> 这是常用的模板，一般为三个参数，也就是Matrix<矩阵变量类型，行数，列数>.

　　　　　　　　　　　 完整的可选模板参数定义如下

　　　　　　　　　　　 Matrix<typename Scalar, //标量类型

　　　　　　　　　　　　　　  int RowsAtCompileTime, //行数

　　　　　　　　　　　　　　  int ColsAtCompileTime,//列数

 　　　　　　　　　　　　　　 int Options = 0,//位域

　　　　　　　　　　　　         int MaxRowsAtCompileTime = RowsAtCompileTime,//最大行数

　　　　　　　　　　　　　　  int MaxColsAtCompileTime = ColsAtCompileTime> //最大列数

 

使用Eigen库定义一个矩阵: Matrix<int,2,2> 这是一个int类型的2x2矩阵

　　　　　　　　　　　　Matrix<float,3,3>这是一个float类型的3x3矩阵

 

Eigen库中简化了部分以上定义的过程，一般用于固定尺寸的矩阵的定义。

例如：  Matrix2f,Matrix3f,Matrix4f  float类型的2x2,3x3,4x4的矩阵(可见结尾部分为f）

     同理Matrix2d,Matrix3d,Matrix4d,Matrix2i,Matrix3i,Matrix4i,只需要看最后结尾的字母，即可明白变量类型(double,int)

Eigen还有个常用的概念，向量，向量是矩阵中的特殊情况，表现为有一行或一列，也就是行向量和列向量，最常见的情况是只有一列，表现方式有：

　　　　　　　　　　　  typedef Matrix<float, 3, 1> Vector3f;  //列向量

　　　　　　　　　　　  typedef Matrix<int, 1, 2> RowVector2i; //行向量

 

接下来说明它们各自的赋值方式以及特殊情况：

静态矩阵下有如下的初始化方式:  Vector2i myvector(1,2);  表示初始化一个列向量为 或者 Vector2f myvector(1.0,2.0); 表示初始化一个列向量为

 

向量能这样初始化，但Matrix就不行了，比如Matrix3f a(3,3)虽然编译能够通过，不会报错，但是这样的传递参数是无效的， 在官方文档有解释：In order to offer a uniform API across fixed-size and dynamic-size matrices, it is legal to use these constructors on fixed-size matrices, even if passing the sizes is useless in this case. 意思是：为了在固定大小和动态大小的矩阵上提供统一的API，在固定大小的矩阵上使用这些构造函数是合法的，即使在这种情况下传递大小是无用的。

 

所以只能使用规定的输入方法： Matrix3f a;

　　　　　　　　　　　　　　 a<<1,2,3,

　　　　　　　　　　　　　　       4,5,6,

　　　　　　　　　　　　　　　　7,8,9;

 

说完静态矩阵，接下来说动态矩阵：typedef Matrix <double,Dynamic,Dynamic> MatrixXd;

看如下对比即可明白：

一般Matrix4f mymatrix; 等价于 float mymatrix[16];
一般MatrixXf mymatrix(rows,columns); 等价于 float *mymatrix = new float[rows*columns];

 

所以有 MatrixXf a(2,2) 即定义一个2x2的矩阵，而且Eigen库有访问矩阵中值的特定方式。

如，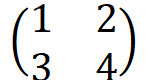 

 

 

访问第一行第一个元素 即 a(0,1) ,也可 a(0,1) = x 为第一行第一个元素赋值。

如：

#include <iostream>
#include <Eigen/Dense>
 
using namespace Eigen;
 
int main()
{
  MatrixXd m(2,2);
  m(0,0) = 3;
  m(1,0) = 2.5;
  m(0,1) = -1;
  m(1,1) = m(1,0) + m(0,1);
  std::cout << "Here is the matrix m:\n" << m << std::endl;
  VectorXd v(2);
  v(0) = 4;
  v(1) = v(0) - 1;
  std::cout << "Here is the vector v:\n" << v << std::endl;
}

Output:

Here is the matrix m:
  3  -1
2.5 1.5
Here is the vector v:
4
3

 

 

像这类动态分配大小的矩阵，有 resize()方法，可以重新定义大小，这篇代码写的很清楚：

#include <iostream>
#include <Eigen/Dense>
 
using namespace Eigen;
 
int main()
{
  MatrixXd m(2,5);
  m.resize(4,3);
  std::cout << "The matrix m is of size "
            << m.rows() << "x" << m.cols() << std::endl;
  std::cout << "It has " << m.size() << " coefficients" << std::endl;
  VectorXd v(2);
  v.resize(5);
  std::cout << "The vector v is of size " << v.size() << std::endl;
  std::cout << "As a matrix, v is of size "
            << v.rows() << "x" << v.cols() << std::endl;
}

Output:

The matrix m is of size 4x3
It has 12 coefficients
The vector v is of size 5
As a matrix, v is of size 5x1

 

 然后说明一下固定尺寸与动态尺寸的选择问题，也就是什么时候静态分配最好，什么时候动态分配最好。

 对于非常小的尺寸，尽可能使用Fixed（一般定义为小于等于16），这种情况下使用Fixed尺寸性能更加优越,因为它可以让Eigen避免动态内存分配和展开循环，对于较大尺寸的话就使用dynamic尺寸，

 当然，使用固定大小的局限性在于，只有在编译时知道大小时才有可能。另外，对于足够大的尺寸，比如说大于或等于32的尺寸，使用固定尺寸的性能优势就变得微不足道了。更糟糕的是，如果试图在函数中使用固定大小创建一个非常大   的矩阵，可能会导致堆栈溢出，因为Eigen会尝试将数组作为一个局部变量自动分配，而这通常是在堆栈中完成的。最后，根据不同的情况，当使用动态大小时，Eigen还可以更积极地尝试矢量化（使用SIMD指令）。

 

 最后解释一下上面说过的可选参数模板

　　Matrix<typename Scalar,
　　　　　　int RowsAtCompileTime,
　　　　　　int ColsAtCompileTime,
　　　　　　int Options = 0,
　　　　　　int MaxRowsAtCompileTime = RowsAtCompileTime,
　　　　　　int MaxColsAtCompileTime = ColsAtCompileTime>

从参数的定义名即可看出来其大概意思。

分析：Matrix<float,Dynamic,Dynamic,0,3,4>  一个不知道大小，但最大行数为3，最大列数为4的矩阵。
从官方文档对于Matrix Optional template parameters 的定义来看，这是一个确定了上限的固定内存矩阵，如果在编译时不知道矩阵的确切大小，但在编译时可以知道一个固定的上限，这样做可以避免动态内存分配。

第三个参数是什么意思呢，在我看来是一个优先级的参数，比如一个矩阵是行优先还是列优先就是使用这个参数，0一般是默认值，不设置任何优先。

比如：Matrix<float,3,3,RowMajor> 就是一个行优先的矩阵。

 

补充Eigen便利类型定义：

Eigen defines the following Matrix typedefs:

• MatrixNt for Matrix<type, N, N>. For example, MatrixXi for Matrix<int, Dynamic, Dynamic>.
• VectorNt for Matrix<type, N, 1>. For example, Vector2f for Matrix<float, 2, 1>.
• RowVectorNt for Matrix<type, 1, N>. For example, RowVector3d for Matrix<double, 1, 3>.

Where:

• N can be any one of 2, 3, 4, or X (meaning Dynamic).
• t can be any one of i (meaning int), f (meaning float), d (meaning double), cf (meaning complex<float>), or cd(meaning complex<double>). The fact that typedefs are only defined for these five types doesn't mean that they are the only supported scalar types. For example, all standard integer types are supported, see Scalar types.