多线程ForkJoin-分治思想

一、ForkJoin

ForkJoin是由JDK1.7后提供多线并发处理框架。ForkJoin的框架的基本思想是分而治之。什么是分而治之？分而治之就是将一个复杂的计算，按照设定的阈值进行分解成多个计算，然后将各个计算结果进行汇总。相应的ForkJoin将复杂的计算当做一个任务。而分解的多个计算则是当做一个子任务。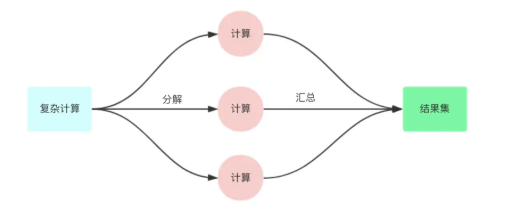

 

二、ForkJoin的使用

使用ForkJoin框架，需要创建一个ForkJoin的任务，而ForkJoinTask是一个抽象类，我们不需要去继承ForkJoinTask进行使用。因为ForkJoin框架为我们提供了RecursiveAction和RecursiveTask。我们只需要继承ForkJoin为我们提供的抽象类的其中一个并且实现compute方法。

关键代码为：

// 多线程处理（线程数默认等于CPU核心数量）
        ForkJoinPool forkJoinPool = new ForkJoinPool();
        AnnexImportTask task = new AnnexImportTask(annexList, provider,annexSecretkeyDaoImp, 0, annexList.size());
        forkJoinPool.submit(task);
        try {
            while(forkJoinPool.getActiveThreadCount() != 0) {
                Thread.currentThread().sleep(100);
            }
        } catch (Exception e) {
            e.printStackTrace();
        }
        // 关闭线程池
        forkJoinPool.shutdown();

public class AnnexImportTask extends RecursiveAction {

    private static final long serialVersionUID = 10000000000000L;

    protected static final Logger logger = LoggerFactory.getLogger(AnnexImportTask.class);

    private List<Annex> annexList;
    
    private BlobContainerProvider provider;
    
    private AnnexSecretkeyDaoImp annexSecretkeyDaoImp;
    
    //单个线程中，可执行的任务队列数最大值
    private int threshold = 1000;
    
    int start;
    
    int end;
    
    //构造方法传参
    public AnnexImportTask(List<Annex> annexList,BlobContainerProvider provider, AnnexSecretkeyDaoImp annexSecretkeyDaoImp,int start, int end) {
        this.annexList = annexList;
        this.provider = provider;
        this.annexSecretkeyDaoImp = annexSecretkeyDaoImp;
        this.start = start;
        this.end = end;
    }

    //重写compute方法
    @Override
    protected void compute() {
        if (end - start < threshold) {
            for (int i = start; i < end; i++) {
                importAnnex(annexList.get(i));//子任务执行的具体操作
            }
        } else {
            int middle = (start + end) / 2;
            AnnexImportTask left = new AnnexImportTask(annexList, provider, annexSecretkeyDaoImp,start, middle);
            AnnexImportTask right = new AnnexImportTask(annexList, provider, annexSecretkeyDaoImp, middle, end);
            left.fork();
            right.fork();
        }
    }

    //具体业务代码，本例子为实际场景中的上传附件
    private void importAnnex(Annex e) {
        String secretkey = "0";
        InputStream binaryStream;
        InputStream encodingToStream;
        GamsAnnexSecretkey gamsAnnexSecretkey;
        if (e.getAnnexData() != null && e.getBizPath() != null) {
            try {
                binaryStream = ((oracle.sql.BLOB) e.getAnnexData()).getBinaryStream();
                EncryptUtil.setKey(secretkey);
                encodingToStream = EncryptUtil.encodingToStream(binaryStream);
                // 保存到文件服务器
                provider.getContainer(e.getBizPath()).uploadFromStream(e.getFilePath(), encodingToStream);
                // 保存加密的秘钥
                gamsAnnexSecretkey = new GamsAnnexSecretkey(UUID.randomUUID(), DataType.toUUID(e.getId()), secretkey == "0" ? 0 : 1, secretkey);
                annexSecretkeyDaoImp.save(gamsAnnexSecretkey);
            } catch (Exception ex) {
                logger.info(ex.getMessage());
            }
        }
    }
}

 

三、RecursiveTask和RecursiveAction区别

RecursiveTask

通过源码的查看我们可以发现RecursiveTask在进行exec之后会使用一个result的变量进行接受返回的结果。而result返回结果类型是通过泛型进行传入。也就是说RecursiveTask执行后是有返回结果。

附上源码：
源码中有斐波拉切数列的示例代码：Fibonacci 

/*
 * ORACLE PROPRIETARY/CONFIDENTIAL. Use is subject to license terms.
 *
 *
 *
 *
 *
 *
 *
 *
 *
 *
 *
 *
 *
 *
 *
 *
 *
 *
 *
 *
 */

/*
 *
 *
 *
 *
 *
 * Written by Doug Lea with assistance from members of JCP JSR-166
 * Expert Group and released to the public domain, as explained at
 * http://creativecommons.org/publicdomain/zero/1.0/
 */

package java.util.concurrent;

/**
 * A recursive result-bearing {@link ForkJoinTask}.
 *
 * <p>For a classic example, here is a task computing Fibonacci numbers:
 *
 *  <pre> {@code
 * class Fibonacci extends RecursiveTask<Integer> {
 *   final int n;
 *   Fibonacci(int n) { this.n = n; }
 *   Integer compute() {
 *     if (n <= 1)
 *       return n;
 *     Fibonacci f1 = new Fibonacci(n - 1);
 *     f1.fork();
 *     Fibonacci f2 = new Fibonacci(n - 2);
 *     return f2.compute() + f1.join();
 *   }
 * }}</pre>
 *
 * However, besides being a dumb way to compute Fibonacci functions
 * (there is a simple fast linear algorithm that you'd use in
 * practice), this is likely to perform poorly because the smallest
 * subtasks are too small to be worthwhile splitting up. Instead, as
 * is the case for nearly all fork/join applications, you'd pick some
 * minimum granularity size (for example 10 here) for which you always
 * sequentially solve rather than subdividing.
 *
 * @since 1.7
 * @author Doug Lea
 */
public abstract class RecursiveTask<V> extends ForkJoinTask<V> {
    private static final long serialVersionUID = 5232453952276485270L;

    /**
     * The result of the computation.
     */
    V result;

    /**
     * The main computation performed by this task.
     * @return the result of the computation
     */
    protected abstract V compute();

    public final V getRawResult() {
        return result;
    }

    protected final void setRawResult(V value) {
        result = value;
    }

    /**
     * Implements execution conventions for RecursiveTask.
     */
    protected final boolean exec() {
        result = compute();
        return true;
    }

}

RecursiveAction

RecursiveAction在exec后是不会保存返回结果，因此RecursiveAction与RecursiveTask区别在与RecursiveTask是有返回结果而RecursiveAction是没有返回结果。

附上源码：

源码中有排序示例代码：SortTask ；平方和示例代码：sumOfSquares

/*
 * ORACLE PROPRIETARY/CONFIDENTIAL. Use is subject to license terms.
 *
 *
 *
 *
 *
 *
 *
 *
 *
 *
 *
 *
 *
 *
 *
 *
 *
 *
 *
 *
 */

/*
 *
 *
 *
 *
 *
 * Written by Doug Lea with assistance from members of JCP JSR-166
 * Expert Group and released to the public domain, as explained at
 * http://creativecommons.org/publicdomain/zero/1.0/
 */

package java.util.concurrent;

/**
 * A recursive resultless {@link ForkJoinTask}.  This class
 * establishes conventions to parameterize resultless actions as
 * {@code Void} {@code ForkJoinTask}s. Because {@code null} is the
 * only valid value of type {@code Void}, methods such as {@code join}
 * always return {@code null} upon completion.
 *
 * <p><b>Sample Usages.</b> Here is a simple but complete ForkJoin
 * sort that sorts a given {@code long[]} array:
 *
 *  <pre> {@code
 * static class SortTask extends RecursiveAction {
 *   final long[] array; final int lo, hi;
 *   SortTask(long[] array, int lo, int hi) {
 *     this.array = array; this.lo = lo; this.hi = hi;
 *   }
 *   SortTask(long[] array) { this(array, 0, array.length); }
 *   protected void compute() {
 *     if (hi - lo < THRESHOLD)
 *       sortSequentially(lo, hi);
 *     else {
 *       int mid = (lo + hi) >>> 1;
 *       invokeAll(new SortTask(array, lo, mid),
 *                 new SortTask(array, mid, hi));
 *       merge(lo, mid, hi);
 *     }
 *   }
 *   // implementation details follow:
 *   static final int THRESHOLD = 1000;
 *   void sortSequentially(int lo, int hi) {
 *     Arrays.sort(array, lo, hi);
 *   }
 *   void merge(int lo, int mid, int hi) {
 *     long[] buf = Arrays.copyOfRange(array, lo, mid);
 *     for (int i = 0, j = lo, k = mid; i < buf.length; j++)
 *       array[j] = (k == hi || buf[i] < array[k]) ?
 *         buf[i++] : array[k++];
 *   }
 * }}</pre>
 *
 * You could then sort {@code anArray} by creating {@code new
 * SortTask(anArray)} and invoking it in a ForkJoinPool.  As a more
 * concrete simple example, the following task increments each element
 * of an array:
 *  <pre> {@code
 * class IncrementTask extends RecursiveAction {
 *   final long[] array; final int lo, hi;
 *   IncrementTask(long[] array, int lo, int hi) {
 *     this.array = array; this.lo = lo; this.hi = hi;
 *   }
 *   protected void compute() {
 *     if (hi - lo < THRESHOLD) {
 *       for (int i = lo; i < hi; ++i)
 *         array[i]++;
 *     }
 *     else {
 *       int mid = (lo + hi) >>> 1;
 *       invokeAll(new IncrementTask(array, lo, mid),
 *                 new IncrementTask(array, mid, hi));
 *     }
 *   }
 * }}</pre>
 *
 * <p>The following example illustrates some refinements and idioms
 * that may lead to better performance: RecursiveActions need not be
 * fully recursive, so long as they maintain the basic
 * divide-and-conquer approach. Here is a class that sums the squares
 * of each element of a double array, by subdividing out only the
 * right-hand-sides of repeated divisions by two, and keeping track of
 * them with a chain of {@code next} references. It uses a dynamic
 * threshold based on method {@code getSurplusQueuedTaskCount}, but
 * counterbalances potential excess partitioning by directly
 * performing leaf actions on unstolen tasks rather than further
 * subdividing.
 *
 *  <pre> {@code
 * double sumOfSquares(ForkJoinPool pool, double[] array) {
 *   int n = array.length;
 *   Applyer a = new Applyer(array, 0, n, null);
 *   pool.invoke(a);
 *   return a.result;
 * }
 *
 * class Applyer extends RecursiveAction {
 *   final double[] array;
 *   final int lo, hi;
 *   double result;
 *   Applyer next; // keeps track of right-hand-side tasks
 *   Applyer(double[] array, int lo, int hi, Applyer next) {
 *     this.array = array; this.lo = lo; this.hi = hi;
 *     this.next = next;
 *   }
 *
 *   double atLeaf(int l, int h) {
 *     double sum = 0;
 *     for (int i = l; i < h; ++i) // perform leftmost base step
 *       sum += array[i] * array[i];
 *     return sum;
 *   }
 *
 *   protected void compute() {
 *     int l = lo;
 *     int h = hi;
 *     Applyer right = null;
 *     while (h - l > 1 && getSurplusQueuedTaskCount() <= 3) {
 *       int mid = (l + h) >>> 1;
 *       right = new Applyer(array, mid, h, right);
 *       right.fork();
 *       h = mid;
 *     }
 *     double sum = atLeaf(l, h);
 *     while (right != null) {
 *       if (right.tryUnfork()) // directly calculate if not stolen
 *         sum += right.atLeaf(right.lo, right.hi);
 *       else {
 *         right.join();
 *         sum += right.result;
 *       }
 *       right = right.next;
 *     }
 *     result = sum;
 *   }
 * }}</pre>
 *
 * @since 1.7
 * @author Doug Lea
 */
public abstract class RecursiveAction extends ForkJoinTask<Void> {
    private static final long serialVersionUID = 5232453952276485070L;

    /**
     * The main computation performed by this task.
     */
    protected abstract void compute();

    /**
     * Always returns {@code null}.
     *
     * @return {@code null} always
     */
    public final Void getRawResult() { return null; }

    /**
     * Requires null completion value.
     */
    protected final void setRawResult(Void mustBeNull) { }

    /**
     * Implements execution conventions for RecursiveActions.
     */
    protected final boolean exec() {
        compute();
        return true;
    }

}

四、ForJoin注意点

使用ForkJoin将相同的计算任务通过多线程的进行执行。从而能提高数据的计算速度。在google的中的大数据处理框架mapreduce就通过类似ForkJoin的思想。通过多线程提高大数据的处理。但是我们需要注意：

• 使用这种多线程带来的数据共享问题，在处理结果的合并的时候如果涉及到数据共享的问题，我们尽可能使用JDK为我们提供的并发容器。
• 在使用JVM的时候我们要考虑OOM的问题，如果我们的任务处理时间非常耗时，并且处理的数据非常大的时候。会造成OOM。
• ForkJoin也是通过多线程的方式进行处理任务。那么我们不得不考虑是否应该使用ForkJoin。因为当数据量不是特别大的时候，我们没有必要使用ForkJoin。因为多线程会涉及到上下文的切换。所以数据量不大的时候使用串行比使用多线程快。

五、ForkJoin工作窃取（work-stealing）

ForkJoin在实际使用中，也可能存在一些问题，而最常见的就是存在数据倾斜问题，即分成的每个子任务不能保证数据都同样大小。

我们将任务进行分解成多个子任务的时候，由于子任务数据量不能保证一样，所以每个子任务的处理时间都不一样。例如分别有子任务A和B。如果子任务A的1ms的时候已经执行，子任务B还在执行。那么如果我们子任务A的线程等待子任务B完毕后在进行汇总，那么子任务A线程就会在浪费执行时间，最终的执行时间就以最耗时的子任务为准。而如果我们的子任务A执行完毕后，处理子任务B的任务，并且执行完毕后将任务归还给子任务B。这样就可以提高执行效率。而这种就是工作窃取。

解决这列问题的关键是分解子任务要合理，需要前期给出几种方案，选取最适合的一种。

六、ForkJoin排序

ForkJoin在实际使用中，经常用来对超大数量进行排序，特别的外排法经常使用

public class SortForkJoin {
    /**
     * 排序
     *
     * @param arry
     * @return
     */
    public static int[] sort(int[] arry) {
        if (arry.length == 0) return arry;
        for (int index = 0; index < arry.length - 1; index++) {
            int pre_index = index;
            int currentValue = arry[index + 1];
            while (pre_index >= 0 && arry[pre_index] > currentValue) {
                arry[pre_index + 1] = arry[pre_index];
                pre_index--;
            }
            arry[pre_index + 1] = currentValue;
        }
        return arry;
    }

    /**
     * 组合
     *
     * @param left
     * @param right
     * @return
     */
    public static int[] merge(int[] left, int[] right) {
        int[] result = new int[left.length + right.length];
        for (int resultIndex = 0, leftIndex = 0, rightIndex = 0; resultIndex < result.length; resultIndex++) {
            if (leftIndex >= left.length) {
                result[resultIndex] = right[rightIndex++];
            } else if (rightIndex >= right.length) {
                result[resultIndex] = left[leftIndex++];
            } else if (left[leftIndex] > right[rightIndex]) {
                result[resultIndex] = right[rightIndex++];
            } else {
                result[resultIndex] = left[leftIndex++];
            }
        }
        return result;
    }


     static  class SortTask extends RecursiveTask<int[]> {
        private int threshold;
        private int start;
        private int end;
        private int segmentation ;
        private int[] src;

        public SortTask(int[] src,int start,int end,int segmentation){
            this.src = src;
            this.start = start;
            this.end = end;
            this.threshold = src.length/segmentation;
            this.segmentation = segmentation;
        }

        @Override
        protected int[] compute() {
            if((end - start) <threshold){
               int mid =  (end-start)/2;
               SortTask leftTask = new SortTask(src,start,mid,segmentation);
               SortTask rightTask = new SortTask(src,mid+1,end,segmentation);
               invokeAll(leftTask,rightTask);
               return SortForkJoin.merge(leftTask.join(),rightTask.join());
            }else{
               return  SortForkJoin.sort(src);
            }
        }
    }

    @Test
    public void test() {
        int[]  array = MakeArray.createIntArray();
        ForkJoinPool forkJoinPool= new ForkJoinPool();
        SortTask sortTask =new SortTask(array,0,array.length-1,1000);
        long start = System.currentTimeMillis();
        forkJoinPool.execute(sortTask);
        System.out.println(
                " spend time:"+(System.currentTimeMillis()-start)+"ms");
    }

}